
- •Глава 1. Основные понятия и принципы электродинамики.
- •§1. Заряд. Плотность заряда. Плотность тока.
- •§2. Закон сохранения заряда
- •§3. Электромагнитное поле. Напряженность электромагнитного поля. Индукция магнитного поля.
- •§4. Уравнения Максвелла для системы зарядов в вакууме.
- •§5. Интегральная формула уравнений Максвелла.
- •§6. Связь уравнений Максвелла и эмпирических законов электродинамики.
- •§7. Ток смещения.
- •§8. Уравнение Максвелла для поля в веществе. Материальные уравнения.
- •§9. Потенциалы электромагнитного поля.
- •§10. Калибровочная инвариантность потенциалов.
- •§11. Калибровка Кулона (поперечная).
- •§12. Уравнения Максвелла-Лоренца для системы зарядов и поля в вакууме.
- •§13. Закон сохранения энергии в электромагнитном поле.
- •§14. Закон сохранения импульса в электромагнитном поле.
- •§15. Закон сохранения энергии электромагнитного поля в веществе.
- •Глава 2. Специальная теория относительности.
- •§16. Исторические предпосылки возникновения специальная теория относительности (сто).
- •Основные черты классических возникновений в физике конца 19 века.
- •Преобразования Галилея.
- •III. Попытки определения абсолютной скорости. Опыт Майкельсона.
- •§17. Постулаты теории относительности.
- •§18. Преобразования Лоренца.
- •§19. Некоторые кинематические следствия из преобразований Лоренца. Пространственные и временные промежутки.
- •Временные промежутки. Замедление времени.
- •Релятивистский закон преобразования скоростей.
- •§20. Абсолютные величины в сто. Интервал и собственное время.
- •§21 Инвариантность физических законов относительно преобразований Лоренца.
- •2. Четырехмерные векторы и тензоры. Четырехмерные скорость и ускорение.
- •Элементы механики теории относительности.
- •§1. Уравнения динамики материальной точки.
- •§2. Импульс, энергия и масса в релятивистской механике.
- •Глава 3. Релятивистская электродинамика.
- •§1. Инвариантность заряда. Четырех мерный ток и уравнение непрерывности.
- •§2. Релятивистски-инвариантная форма уравнений для потенциалов.
- •§3. Тензор электромагнитного поля и уравнения Максвелла.
- •I группа
- •II группа
- •§4. Преобразование векторов электромагнитного поля. Инварианты поля.
- •§5. Четырёхмерное обобщение силы Лоренца. Инвариантная форма записи законов сохранения.
- •§6. Инвариантность фазы плоской монохроматической волны. Четырех мерный вектор.
- •§7. Эффект Доплера и аберрация света.
- •§8. Лагранжиан и Гамильтониан заряженной частицы в электромагнитном поле.
- •§9. Запаздывающие потенциалы.
- •§10. Потенциалы Ликнара – Вихерта и поле точечного заряда.
- •§11. Полная мощность, излучаемая ускоренно движущихся зарядом. Формулы Лармона и Лиенара.
- •§12. Движение заряженных частиц в линейных и циклических условиях.
- •Глава 3. Глава Поля ограниченного распределения зарядов (поля островных сил).
- •§1. Потенциал электромагнитного поля вдали от излучателей в дипольном приближении.
- •§2.Электромагнитное поле дипольного излучения вдали от излучателя.
- •§3.Угловое распределение излучения ускоряемого заряда
- •§3. Дипольное излучение простейших систем.
- •§4. Квадрупольное и магнитное дипольное излучение.
- •§45. Спектральное разложение излучения.
- •§46. Распространение электромагнитных волн вдали от излучателя Плоские волны.
- •§47. Поляризация плоской волны.
- •§48. Интерференция и образование волновых пакетов. Групповая скорость.
- •§49. Реакция излучения.
- •§501. Рассеяние света на свободных зарядах. Формула Томсона.
- •§502. Рассеяние света на свободных зарядах. Формула Томсона.
- •§51. Максвелловское поле в среде как усредненное микроскопическое.
- •§52. Граничные условия на покоящейся границе раздела сред.
- •§55 Электромагнитные волны в однородной поглощающей изотропной среде. Комплексная диэлектрическая проницаемость.
- •§56 Отражение и преломление плоских волн на границе раздела изотропных сред.
- •§57-58 Поля на поверхности и внутри проводника. Скин-эффект.
- •§ 59 Волноводы
- •§ 60 Резонаторы
- •§ 61. Магнитоактивные среды. Тензор диэлектрической проницаемости плазмы в постоянном магнитном поле.
- •§62. Плоские волны в магнитоактивной плазме.
- •§63. Тензор диэлектрической проницаемости ферритов.
§4. Преобразование векторов электромагнитного поля. Инварианты поля.
Рассмотрим
для простоты случай, когда соответствующие
оси ИСО s
и
![]() взаимно параллельны
относительное движение происходит
вдоль
взаимно параллельны
относительное движение происходит
вдоль
![]() ,
а в начальный момент время
,
а в начальный момент время
![]() начала обоих ИСО совпадают. Тогда
компоненты тензора F
при переходе от
s
к
начала обоих ИСО совпадают. Тогда
компоненты тензора F
при переходе от
s
к
![]() преобразуются
по закону
преобразуются
по закону
![]() (1)
(1)
где
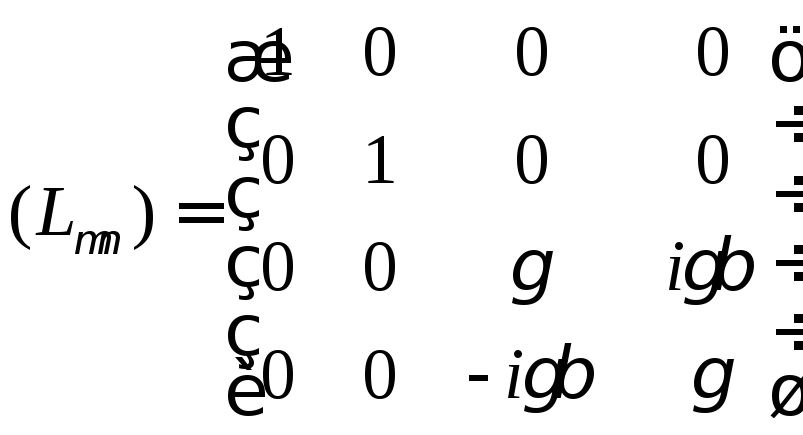

Получим:

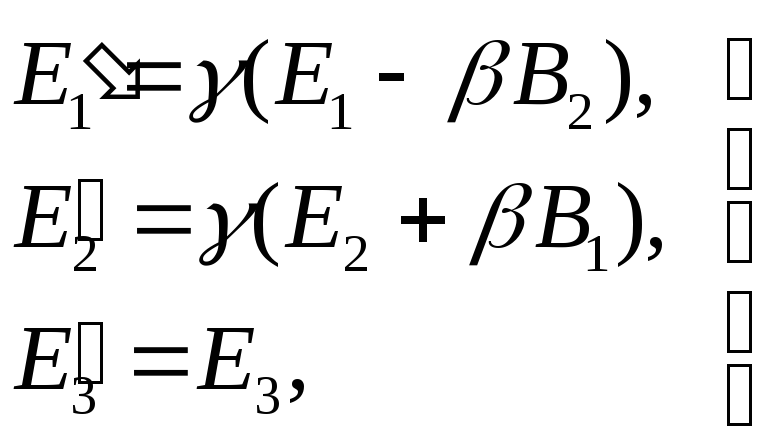 (2)
(2)
 (3)
(3)
Видно,
что
что компоненты
![]() и
и
![]()
параллельные скорости относительного
движения систем отсчета
не изменяются, а перпендикуллярные -
параллельные скорости относительного
движения систем отсчета
не изменяются, а перпендикуллярные -
![]() и
и
![]() - преобразуются в соответствии с
полученными формулами. Разлагая E
и B
на продольную и поперечную составляющую
- преобразуются в соответствии с
полученными формулами. Разлагая E
и B
на продольную и поперечную составляющую
![]()
![]()
непосредственной проверкой убеждаемся, что :
 (4)
(4)
 (5)
(5)
Найдём
инварианты тензора
![]() Ими
являются, например, коэффициенты
характеристического уравнения
Ими
являются, например, коэффициенты
характеристического уравнения
![]()
В
явном виде это уравнение 4-й степени
относительно
![]() имеет вид:
имеет вид:
![]()
![]()
Так
как
![]() ,
то
,
то
![]()
Это
означает
что
![]() и характеристическое уравнение примает
вид
и характеристическое уравнение примает
вид
![]() (7)
(7)
Найдем

![]()
Здесь
учтено
что
![]()
а
а
![]() - единичный оператор трехмерного.
- единичный оператор трехмерного.
Очевидно
![]()
Следовательно величина
![]() (9)
(9)
- инвариант преобразований Лоренца
Согласно теореме Гамильтона-Кэли любой тензор удовлетворяет своему характеристическому уравнению, т.е. имеет место соотношение
![]()
Отсюда
следует, что оператор
![]() можно вычислить следующим образом:
можно вычислить следующим образом:
 (10)
(10)
Найдем
![]() :
:

Таким
образом
определитель
![]() равен
равен
![]() (11)
(11)
Значит
![]() -
инвариант. Фактически
и величина
-
инвариант. Фактически
и величина
![]() является инвариантом преобразования
Лоренца
но она допускает изменение знака
является инвариантом преобразования
Лоренца
но она допускает изменение знака
Инварианты
![]() ,
,
![]() (12)
(12)
отличаются
тем, что
![]() -
скаляр, а
-
скаляр, а
![]() - псевдоскаляр. При отражении трёх
пространственных осей или при инверсии
времени
- псевдоскаляр. При отражении трёх
пространственных осей или при инверсии
времени
![]() не изменяется, а
не изменяется, а
![]() меняет знак.
меняет знак.
Из
существования инвариантов электромагнитного
поля вытекает ряд следствий
Пусть для простоты
![]() и
и
![]() вещественные векторы
Тогда
вещественные векторы
Тогда
Если в некоторой ИСО
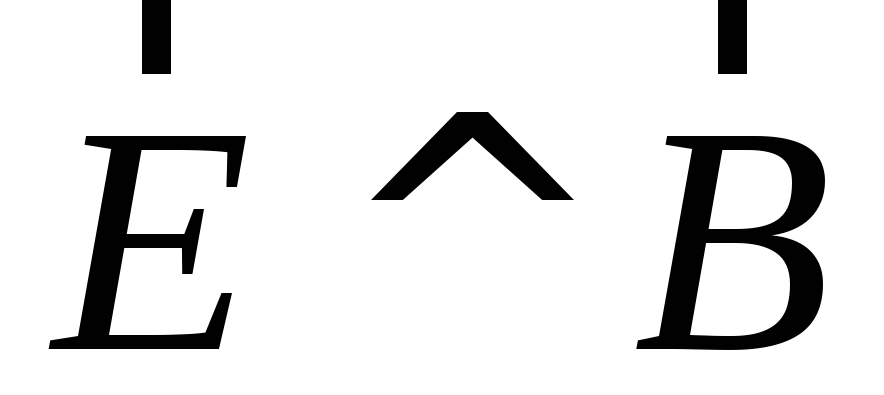 ,
то и в любой другой ИСО
,
то и в любой другой ИСО
 .
.Если в некоторой ИСО
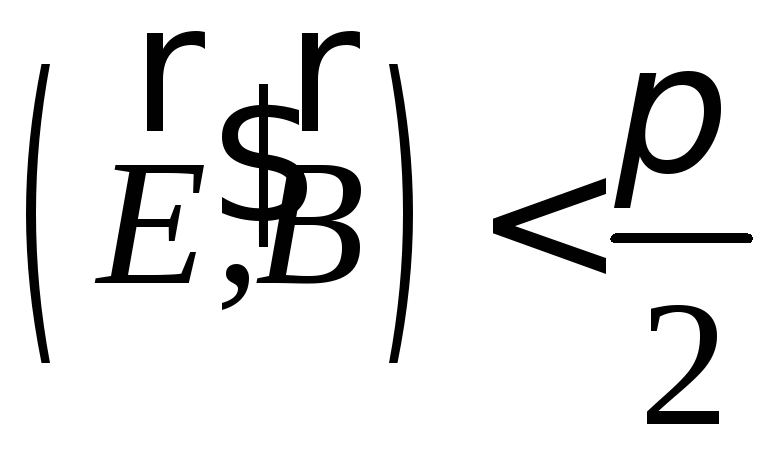 ,
то и в любой другой ИСО
,
то и в любой другой ИСО
 .
.
Если в некоторой ИСО
 ,
то и в любой другой ИСО
,
то и в любой другой ИСО
 .
.Если в некоторой ИСО
 и
и
 ,
то существует такая ИСО, в которой любой
из векторов поля
,
то существует такая ИСО, в которой любой
из векторов поля
 или
или
 равен нулю.
равен нулю.Если в некоторой ИСО
 ,
то и в любой другой ИСО
,
то и в любой другой ИСО
 .
.Если в некоторой ИСО
 ,
то существует такая ИСО, в которой
,
то существует такая ИСО, в которой
 .
.
Замечание:
для поля в веществе, когда
![]() ,
закон преобразования
,
закон преобразования
![]() и
и
![]() получается из (4),(5) заменой
получается из (4),(5) заменой
![]() и
и
![]() .
.
Инвариантами
поля наряду с (12), являются величины
![]() .
.
§5. Четырёхмерное обобщение силы Лоренца. Инвариантная форма записи законов сохранения.
Выпишем
в явном виде её первую составляющую
трёхмерной плотности силы Лоренца:
![]() - равна скорости изменения количества
движения в единице объёма.
- равна скорости изменения количества
движения в единице объёма.
Запишем первую компоненту:
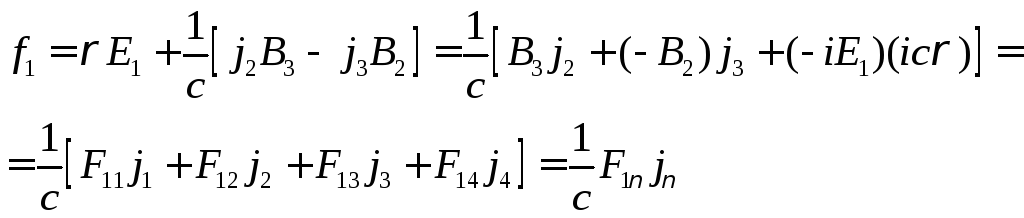
Аналогичного
соотношения получаются и для
![]() ,
так что
,
так что
![]() (1)
(1)
Правые части (1) – представляют собой пространственные составляющие 4-вектора:
![]() (2)
(2)
который называют 4-вектора плотности силы Лоренца.
Выясним физический смысл четвертой составляющей вектора:

![]() (3)
(3)
Т.о.
![]() – эта работа, совершаемая полем под
зарядами в единичном объёме в единицу
времени, т.е. скорость изменения
механической энергии частицы в единице
объёма. Пространственная же часть силы
Лоренца определяет скорость изменения
импульса в единице объёма. Законы
сохранения полной энергии (механической
и электромагнитной) и полного импульса
можно представить в 4-х мерной инвариантной
форме в виде уравнений для пространственной
и временной части единого 4-вектора. А
именно, из уравнений Максвелла:
– эта работа, совершаемая полем под
зарядами в единичном объёме в единицу
времени, т.е. скорость изменения
механической энергии частицы в единице
объёма. Пространственная же часть силы
Лоренца определяет скорость изменения
импульса в единице объёма. Законы
сохранения полной энергии (механической
и электромагнитной) и полного импульса
можно представить в 4-х мерной инвариантной
форме в виде уравнений для пространственной
и временной части единого 4-вектора. А
именно, из уравнений Максвелла:
 (4)
(4)
 (5)
(5)
Следует, что имеет место соотношение:
 (6)
(6)
где
![]() -
некоторый тензор второго ранга, называемый
тензором энергии импульса.
-
некоторый тензор второго ранга, называемый
тензором энергии импульса.
Действительно, из (4) следует, что
 Далее
Далее

(***)
- проверяется непосредственно :
![]()
Таким образом имеем:

Т.о. действительно имеет место (6), причём:
 (7)
(7)
В бескоординатном виде, очевидно
 (7)
(7)
Очевидно,
что
![]()
Т.к.
 ,
,
![]() ,
то
,
то
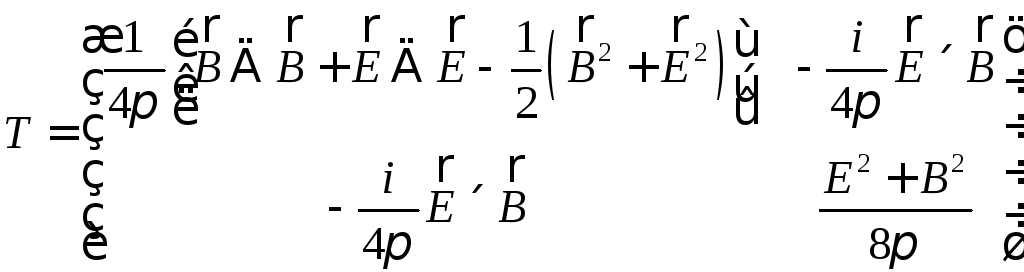 (8)
(8)
Вспоминая
определение тензора максвелловских
натяжений
![]() ,
вектора Пойтинга
,
вектора Пойтинга![]() и плотности импульса
и плотности импульса![]() ,
плотности
,
плотности
энергии
![]() ,
видим, что
,
видим, что
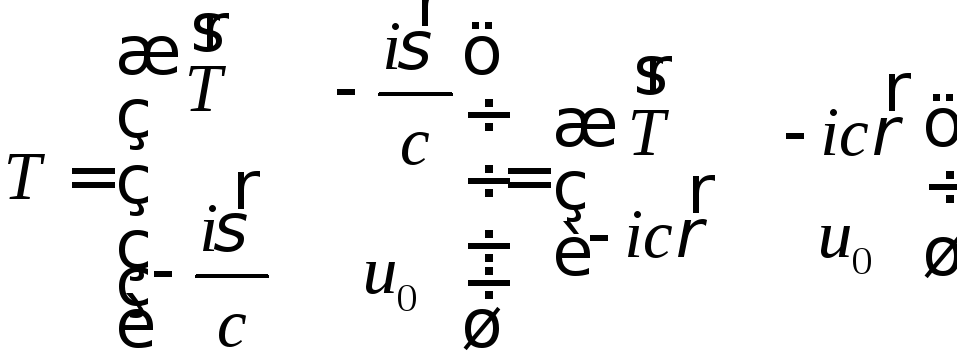 (9)
(9)
Легко
убедиться, что для
![]() из (6) следует
из (6) следует

![]() -
закон сохранения энергии ( в дифференциальной
форме)
-
закон сохранения энергии ( в дифференциальной
форме)
Аналогично
(6) для
![]() приводит к соотношениям, выражающим
закон сохранения импульса.
приводит к соотношениям, выражающим
закон сохранения импульса.
