§20. Абсолютные величины в сто. Интервал и собственное время.

Возникновение теории относительности привело к крушению представлений об абсолютном характере пространства и времени и установлению относительности пространственных и временных промежутков Отсюда и название – теория относительности.

Однако главная задача СТО – установление абсолютных, независящих от выбора ИСО, законов природы. Эта задача тесно связана с нахождением абсолютных инвариантных величин. Одна из них – скорость света в пустоте. Другим важным инвариантом является так называемый интервал.

Это понятие в СТО обобщает обычные понятия интервала между двумя точками пространства (те расстояния) и интервала между двумя событиями (те промежутка времени).

Пусть в точке пространства с координатами в момент времени происходит некоторое физическое явление, именуемое событием. В другой точке в момент времени происходит другое событие. Тогда пространственно-временным интервалом между этими событиями называется величина:

 (1)

В движущейся системе отсчета будем иметь:

 (2)

Прямыми вычислениями с использованием преобразований Лоренца находим

 (3)

т.е. интервал инвариантен относительно преобразований Лоренца. Значит утверждение “два физических события разделены интервалом ” имеет абсолютный характер. Интервал между двумя событиями, происходящими между бесконечно близкими точками пространства за бесконечно малое время, равен

 (4)

В зависимости от знака подкоренного выражения может быть как вещественным, так и мнимым. Пусть



В этом случае всегда можно найти такую СО, в которой два события происходят в одном и том же месте. Необходимо, чтобы



а это всегда возможно при положительном подкоренном выражении. Поэтому вещественные интервалы называют времениподобными интервалами. В частностиесли два события происходят с одной и той же физической системой, напримерсобытиями являются показания одних и тех же часовто эти события разделены времениподобным интервалом. Действительноза время система может пройти путь , так как её скорость меньше скорости света.

Мнимый интервал называется пространственно подобным. Если два события разделены таким интервалом, то всегда можно найти СО, в которой они происходят в один и тот же момент времени. Для этого необходимо, чтобы выполнялось равенство

,

что всегда возможно при отрицательном подкоренном выражении слева.

Пусть в некоторой точке ИСО происходят два последовательных события, разделенных бесконечно малым промежутком времени . Время измеряется часами, покоящимися в системе , т.е. собственными часами системы . Поэтому - собственное время, прошедшее между двумя событиями. Интервал между этими событиями по определению равен



Таким образом собственное время

(5)

является инвариантом.

Выразим через время dt в произвольной ИСО s относительно которой движется со скоростью :



Таким образом

.

§21 Инвариантность физических законов относительно преобразований Лоренца.

Согласно принципу относительности все физические законы должны быть сформулированы так чтобы они оставались инвариантными относительно преобразований Лоренца – как говорят релятивистски или Лоренц-инвариантными

Законы механики не являются Лоренц-инвариантными, поэтому они должны быть видоизменены. Требование инвариантности физических законов относительно некоторых преобразований не является специфической особенностью СТО. Ясно например что вследствие изотропии пространства, содержание физического закона скажем, второго закона Ньютона

(1)

не может зависеть от ориентации координатных осей. При любом повороте осей в пространстве уравнения (1) остаются неизменными, т.к. каждая из проекций силы и ускорения преобразуется по одному и тому же закону.

Это свойство можно сформулировать так: в классической физике все законы формулируются в виде равенств типа

 (2)

 (3)

 (4)

связывающих величины одинаковой тензорной размерности Например (3) связывает векторы При повороте, в частности вокруг вокруг оси z на угол компоненты радиус-вектора преобразуются по закону

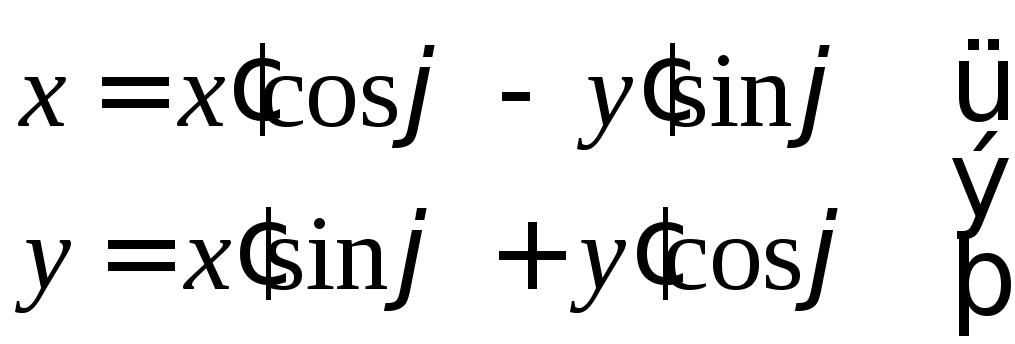(5)

Поскольку по этому закону преобразуются компоненты любых векторов, а не только компоненты радиус-вектора то (3) не нарушается.

Итак любой физический закон должен быть сформулирован так, чтобы он содержал только величины одинаковой тензорной размерности. В классической механике законы преобразования координат которые должны оставлять неизменными физические законы сводятся к следующим:

1. Инвариантность относительно преобразований Галилея

2. Инвариантность относительно пространственных переносов и поворотов систем координат (однородность и изотропия простанства)

3. Инвариантность относительно замены (однородность времени)

4. Инвариантность относительно замены (обратимость времени, указывающая на симметрию законов механики относительно прошлого и будущего).

СТО вместо требования (1) выдвигает более общее требование инвариантности физических законов относительно преобразований Лоренца. Условия (2) - (4) сохраняются и в СТО.

Один из способов, позволяющий установить Лоренц-инвариантную форму физических законов, состоит вследующем

Введем формально величину

 (6)

которую будем называть четвертой координатой или мнимым временем Это мнимая величина не имеющая прямого физического смысла Если обозначить как обычно, то с помощью (6) интервал можно представить в виде

 (7)

Будем считать ортогональными координатами в некотором абстрактном четырехмерном пространстве Преобразование Лоренца – это линейное преобразование этих координат, оставляющее неизменной величину.Но с геометрической точки зрения - суть квадрат расстояния между двумя точками в четырехмерном пространстве. То есть преобразование Лоренца - это такое линейное преобразование которое не изменяет расстояние между двумя точками.в четырехмерном пространстве Из геометрии известно что имеется только два только два таких преобразования –параллельный перенос и вращение. Первое –это тривиальное преобразование сводящееся к изменению начала отсчета системы координат x,y,z,ict. Поэтому единственным нетривиальным линейным преобразованием, оставляющим неизменным интервал – является поворот в четырехмерном пространстве x,y,z,ict.

Такая геометрическая интерпретация преобразований Лоренца принадлежит Минковскому и позволяет непосредственно сделать вывод о релятивистски инвариантной форме физических законов. Соответствующие выражения должны иметь вид

, (8)

где -скаляры, или

, (9)

где - 4-х мерные векторы, =1,2,3,4 и в общем случае

, (10)

где - четырехмерные тензоры произвольного ранга.

При поворотах координатных осей в четырехмерном пространстве Минковского (x,y,z,ict) все величины, входящие в релятивистски-инвариантные выражения, преобразуются по одному закону, поэтому равенства (8)-(10) не нарушаются.

Эти условия инвариантности в четырехмерном пространстве являются непосредственным аналогом условий инвариантности при повороте системы координат в реальном трехмерном пространстве

Представление о четырехмерном пространстве имеет формальный характер, а четвертая координата ict будучи мнимой не имеет непосредственного физического смысла. Тем не менее, введение этой координаты вполне оправданно указывая в частности на неразрывную связь пространства и времени. Заметим что четвертую координату не обязательно вводить как величину мнимую

Убедимся, что преобразование поворота в пространстве(x,y,z,ict) идентично преобразованию Лоренца. Для простоты считаем, что движение происходит в направлении совмещенных осей . Это отвечает повороту в плоскости ипри неизменной ориентации осей и . Если обозначить через угол поворота, то

 (11)

 (12)

Для будем иметь





Отсюда

 (13)

где V – скорость равномерного движения начала координат системы относительно системы .

Из (13) следует что





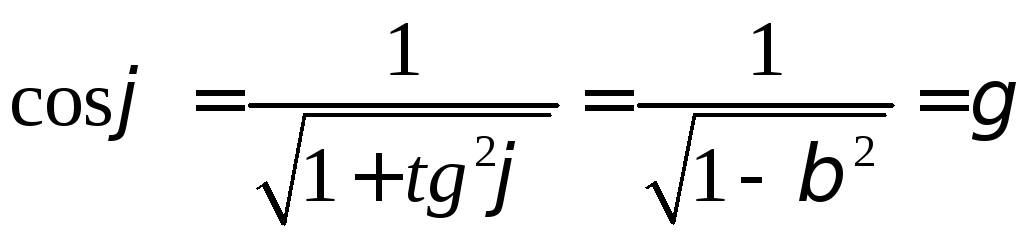
откуда



или 

Эти формулы совпадают с фомулами обратного преобразования Лоренца.