§17. Постулаты теории относительности.

Отрицательные результаты опытов Майкельсона и других экспериментов, направленных на получение прямых доказательств существования эфира, неудовлетворительность последующих попыток объяснения этих результатов привели в конечном итоге к пересмотру ряда исходных понятий классической физики. В результате усилиями в основном Лоренца, Пуанкаре, Эйнштейна и Минковского, была создана так называемая специальная теория относительности (СТО). В основу Эйнштейновской формулировки СТО положено два постулата.

1. Принцип относительности Эйнштейна:

Любое физическое явление протекает одинаково во всех ИСО.

2. Принцип постоянства скорости света:

Во всех ИСО по всем направлениях скорость распространения света в пустоте имеет одно и то же значение равное c.

Принцип относительности является очевидно обобщением принципом относительности Галилея на все физические явления. Так как уравнения Максвелла не инвариантны относительно преобразований Галилея, то в СТО закон преобразования координат и времени должен быть выведен заново. Для этого и служит второй постулат СТО. Его часто называют принципом существования предельной скорости распространения взаимодействия. Если допустить, что существует некоторая предельная скорость движения материальных объектов, то она должна быть одинакова во всех ИСО. Иначе нарушится равноправие ИСО, вытекающее из принципа относительности. Эта скорость равна c и ей обладают например электромагнитные волны в пустоте.

Таким образом в процессе развития физики пришлось отказаться от теории дальнодействия (бесконечная скорость распространения взаимодействия) в пользу теории близкодействия (конечная скорость распространения взаимодействия).

§18. Преобразования Лоренца.

В релятивистской области движения сохраняется во многом модель пространства и времени классической механики. Т.е. пространство трёхмерно и евклидово, непрерывно, однородно и изотропно. Время – одномерно, непрерывно, однородно и однонаправлено. Новым является закон преобразования координат и времени при переходе от одной ИСО к другой. Это так называемые преобразования Лоренца, открытые им ещё до появления СТО. Найдём их, используя упомянутые свойства пространства и времени и постулаты Эйнштейна.

Пустьx, y, z, t и - координаты и время в ИСОs и ,V- скорость движения относительноs. Нет никаких оснований полагать, что время в системах s и совпадают.

1 Из однородности пространства и времени следует что

 (1)

и аналогично для , где- константы. Если бы мы имели, чтои т.д., то связь (1) была бы нелинейной и следовательно закон преобразования был бы неодинаков для разныхx, y, z, t  Но эти коэффициенты конечно могут зависеть от V.

2. Не ограничивая общность рассуждений будем считать, что соответствующие оси координат параллельны и относительное движение происходит вдоль оси x со скоростью V, а начала систем отсчета выбраны так, что при t=0 начало системы (т.е. точка) совпадало с началом системы отсчетаs (точкой x=y=z=0 ) и в этот момент часы в системе показывали . При этом в формуле (1) p=0. Так как плоскости xy и совпадают, то приследуетдля любых. Но это возможно только если,гдеk=const. Ввиду произвольности осей (изотропия пространства), такая же связь с тем же коэффициентом должна быть и для

Запишем преобразования для в виде

(2)

В плоскости , имеемдля любыхy,z.

Подставляя эти ив формулу (2) получим, что

Учитывая, что при следуетнаходим, что



Таким образом,

(3)

3. Системы s иравноправны. Это значит, что формулы перехода изв s должны получаться из формулы (3) заменой V на -V .

(4)

Обратимся сначала к формулам для y и z ((3) и (4)) отличающимся направлением скорости. Вследствие изотропии пространства должно быть k(V)=k(-V). Совершая преобразования от y к и обратно, находим, т.е.. Значение отвечает противоположной ориентации осей, поэтому в соответствии с рисунком  . Подставими(3) в формулу дляx (4). Получим

(5)

Чтобы это выполнялось для всех x и t необходимо, чтобы

(6)

4. Пусть в момент из совпадающих начал системиначинает распространяться сферическая световая волна. Точка пересечения фронта волны с осьюдвижется со скоростью Но свет распространяется во всех системах отсчета с одинаковой скоростью, следовательно , и поделивна(3) получимоткуда

(7)

Чтобы найти рассмотрим уравнение сферического волнового фронта в системахи:

 (8)

Поскольку то

 (9)

С помощью формул (3), (6), (7) находим что

(10)

Здесь опять надо взять знак плюс так как знак минус отвечает противоположному направлению осей и. Собирая воедино все результаты приходим к релятивистским формулам преобразования координат и времени - преобразованиям Лоренца

(11)

Обратные преобразования получаются заменой :

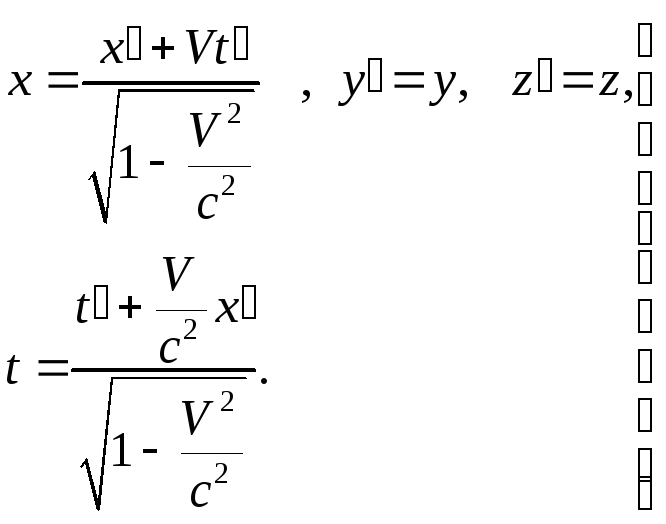(12)

В целях сокращения записи часто используют обозначения , В этих обозначениях преобразования Лоренца принимают вид

(13)

При имееми преобразования Лоренца переходят в преобразования Галилея. Т.о. СТО не отвергает преобразования Галилея как неверные, но включает их в истинные преобразования Лоренца, как частный случай, справедливый для скоростей<<c .