3.1.7. Расчет абсолютных значений энтропии

Прикладное значение постулата Планка состоит в том, что он устанавливает начало отсчета значений энтропии и открывает путь определения абсолютной величины этой термодинамической функции.

Если, например, повышать температуру 1 моля идеального кристалла вещества от 0 до Т при р=1атм, то при отсутствии полиморфных превращений и других изменений фазовых состояний для нахождения энтропии необходимо провести интегрирование уравнения:

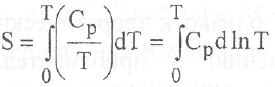
В общем же случае приходится обращаться к более громоздкому выражению:

*) Поскольку, строго говоря, третий закон термодинамики применим только к ограниченному классу веществ, а именно, к чистым бездефектным кристаллам, некоторые авторы (А. Мюстер, Химическая термодинамика, М.: Мир, 1971.—295 с.; с. 196-197,) полагают, что третье начало должно быть сформулировано не в виде закона, а в форме правила, которое на практике "выполняется с достаточной точностью".

74

[p# 75]

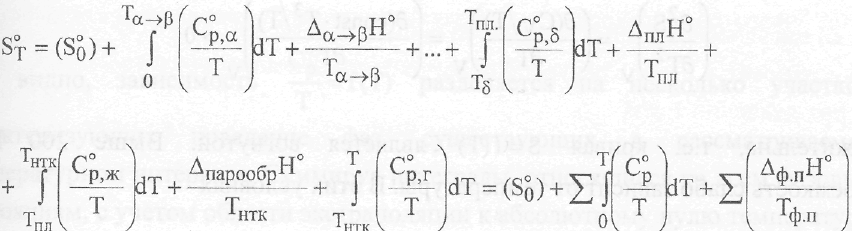
где sq - остаточная или нулевая энтропия; а,р,.,8,... - символы, обозначающие полиморфные модификации кристаллической фазы; Т_нтк - нормальная температура кипения.

Графической иллюстрацией записанного выше уравнения являются данные об энтропиях воды и брома, показанные на рис.11 .

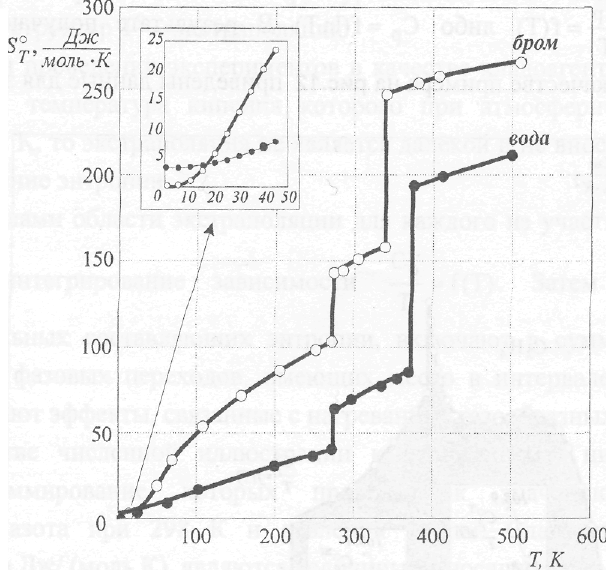
Рис. 11. Температурная зависимость энтропии воды и брома

Как видно из рис.11, зависимость энтропии от температуры имеет сложный характер. В области низких температур, когда теплоемкость возрастает пропорционально температуре в третьей степени, вторая производная энтропии по температуре

3. Критерии (энтропия)

75

[p# 76]

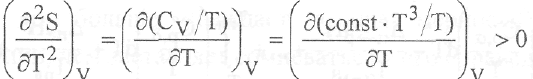
положительна, т.е. кривая S = f (Т) является вогнутой. Выше 200 К теплоемкость слабо зависит от температуры. В этих условиях

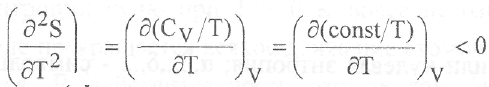
/V

вторая производная отрицательна и наблюдаемая зависимость будет выпуклой. Процедура нахождения абсолютной энтропии веществ основывается на обработке экспериментальных данных о температурной зависимости их теплоемкости. С этой целью массив экспериментальных данных представляют в

Ср координатах —*- = f(T) либо C_p=f(lnT) В результате получают сложную

зависимость. В качестве примера на рис.12 приведены данные для этилена.

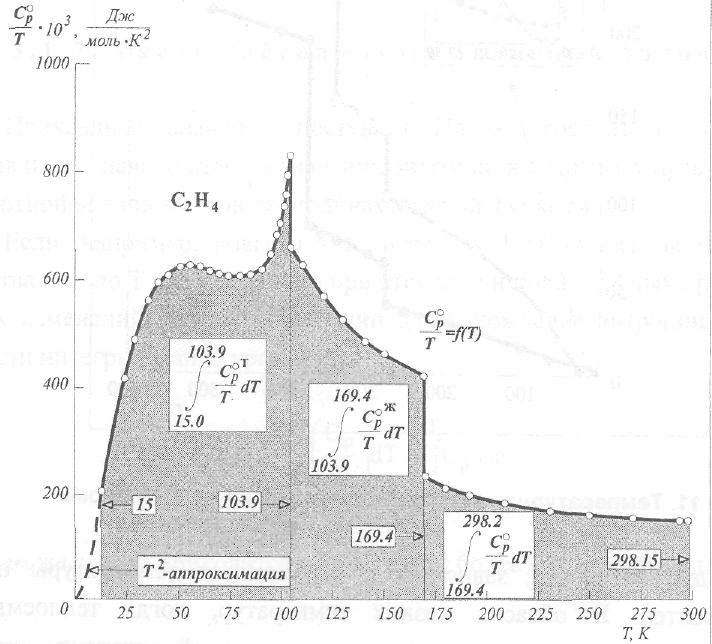
Рис. 12. Интерирование зависимостис целью нахождения величины

м.

Абсолютной энтропии

[p# 77]

76

[p# 78]

с°

V^. rt

Как видно, зависимость —~ = f (Т) разделяется на несколько участков,

характеризующих поведение фаз, существующих в рассматриваемом температурном интервале. Суммируя интегралы, относящиеся ко всем фазовым состояниям, с учетом области экстраполяции к абсолютному нулю температуры и принимая во внимание энтропии всех фазовых переходов, приходим к значению S^gjs-

Современная криогенная техника позволяет производить измерения теплоемкости при весьма низких, но все же отличных от абсолютного нуля температурах. Так как интегрирование должно быть выполнено во всем интервале температур, то всегда существует необходимость экстраполировать данные о теплоемкости к абсолютному нулю температуры. С этой целью в случае трехмерных кристаллических структур используют Т³ - и для слоистых, т.е. двумерных структур Т² - экстраполяцию.

Если при проведении экспериментов в качестве хладоагента применяют жидкий гелий, температура кипения которого при атмосферном давлении составляет 4,22 К, то экстраполяция не является далёкой и не вносит ощутимой ошибки в значение энтропии.

За пределами области экстраполяции для каждого из участков проводят

С°

D

графическое интегрирование зависимости — = f (Т). Затем суммируют

значения отдельных составляющих энтропии, включают в сумму величины энтропии всех фазовых переходов, имеющих место в интервале температур О - Т, и учитывают эффекты, связанные с нагреванием газообразных веществ

В качестве численной иллюстрации к изложенному, ниже указаны величины, суммирование которых приводит к значению энтропии газообразного азота при 298 К и давлении 1 атм. Слагаемыми суммы, выраженными в Дж/ (моль К), являются величины, относящиеся к:

1) экстраполяции экспериментальных данных от 10 К до О К по

^

уравнению Дебая (Т -экстраполяция) 1,92;

2) графическому интегрированию от 10 К до 35.61 К, что отвечает нагреванию твердого азота до температуры фазового превращения

в твердом состоянии 25,25

3. энтропии фазового перехода при 35.61 К 6,43;

4. графическому интегрированию от температуры

фазового перехода до температуры плавления азота при 63.14 К 23,38;

5) энтропии плавления 11,42;

3. Критерии (энтропия) 77

[p# 79]

6) графическому интегрированию в интервале 63.14-77.32 К, которое относится к температурной области существования жидкого

азота при давлении 1 атм 11,41;

7. энтропии парообразования при нормальной температуре кипения 72,13;

8. изобарическому нагреванию азота как идеального газа в интервале 77.32-298.15 К 39.20;

9. поправки на неидеальность поведения газа 0,92 .

В результате получаем S^g ⁼ 192.06 Дж/(моль-К).

Измерения низкотемпературной теплоёмкости очень трудоемки, поэтому массив справочных данных о величинах абсолютных энтропии веществ значительно меньше, чем по стандартным энтальпиям образования.

В некоторых справочных руководствах наряду с данными о S^g (будьте

внимательны: это именно абсолютная энтропия, но не AfS^g) приводятся сведения о высокотемпературных составляющих энтропии Sj - 8298 • Последнее избавляет от необходимости интегрирования в интервале температур 298 - Т и открывает возможность расчета Sj по уравнению:

Если требуется рассчитать величину мольной энтропии при давлении, отличном от стандартного, то вычисления проводят по уравнению*):

•

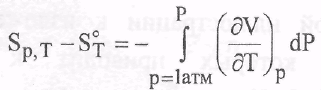
*) Вывод уравнения дан в разделе 3.2.8.

3. Критерии (энтропия) 78

Как уже отмечалось, для конденсированных фаз влиянием давления на величину энтропии можно пренебречь. В случае идеальных газов расчет осуществляют по уравнению:

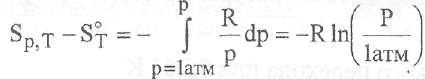
[p# 80]

Для вычисления энтропии реальных газов необходимо знать

fdV] соответствующее уравнение состояния и, представив — как функцию

давления, взять интеграл, приведенный выше.

Так как данные об абсолютных энтропиях конденсированных фаз сравнительно (с информацией о стандартных энтальпиях образования) немногочисленны, полезно принять во внимание эмпирическое уравнение Веннера, позволяющее оценить или уточнить сомнительное по тем или иным причинам значение энтропии. Это уравнение, справедливое для ряда однотипных неорганических веществ, имеет вид:

S = AlgM + B,

где М - - молярная масса соединения, А и В - эмпирические константы, характеризующие рассматриваемый ряд веществ.

Отметим здесь же, что для газообразных веществ, состояние которых близко к идеальному, значения энтропии при любых температурах и давлениях могут быть вычислены методами статистической термодинамики из данных о пространственном строении молекулы и величинах ее молекулярных постоянных. Соответствующие уравнения будут выведены при рассмотрении свойств идеальных газов.