3 .1.1.С в о и ств а энтропии. Энтропия как критерий направленности самопроизвольных процессов и равновесия в изолированных системах

Энтропия является экстенсивным свойством вещества и аддитивным свойством сложной системы, включающей несколько веществ или подсистем. Это означает, что энтропия пропорциональна массе (числу молей) вещества "i" и при наличии в системе нескольких веществ находится суммированием произведения мольной энтропии на число молей данного вещества:

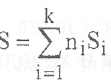
Размерность энтропии Дж/К совпадает с размерностью теплоемкости. Величину энтропии принято относить к молю вещества, что приводит к Дж/( моль К).

В случае изолированных систем, для которых исключён обмен с окружающей средой массой и любыми видами энергии, можно записать:

откуда следует, что

энтропия изолированной системы или увеличивается, или после достижения максимума остается постоянной.

Графически это поясняет рис.10 .

64

[p# 71]

Рис.10, Изменения энтропии изолированной системы

Если изолированная система достигла состояния равновесия, то изменить его можно только при условии отмены ограничения, исключающего возможность обмена энергией с окружающей средой. В неизолированных системах, для которых обмен энергией и массой имеет место, знак изменения энтропии системы может быть как больше, так и меньше нуля.

3.1.2. Связь энтропии с параметрами

состояния(Т,р,У) в процессах с участием идеальных газов

Для систем, в которых осуществляются обратимые превращения в условиях постоянства объема или давления можно записать:

Так как

то

Поскольку теплоемкость индивидуальных веществ является величиной

3. Критерии (энтропия)

65

[p# 72]

положительной, то энтропия вещества должна всегда возрастать с повышением температуры.

Для идеальных газов интегрирование записанных уравнений приводит к выражениям, описывающим изменение энтропии в процессах:

2) изохорного нагревания

1) изобарного нагревания:

где п - число молей газа, участвующих в процессе.

Остановимся теперь на анализе зависимостей энтропии от объема и давления при фиксированной температуре. Рассмотрим на данном этапе эти зависимости применительно к описанию поведения идеального газа*). Как уже отмечалось, для обратимых процессов

Поскольку

то для процессов с участием моля идеального газа при постоянстве температуры и давления будем иметь

pdV=TdS и, следовательно

*) В общем виде эти уравнения будут выведены в разделе 3.2.8 и имеют вид:

[p# 73]

После разделения переменных и интегрирования в пределах V_: и V₂ получаем:

Отсюда следует, что энтропия газа возрастает с увеличением объема и уменьшается при возрастании давления. Это вполне понятно в терминах молекулярной упорядоченности системы. Действительно, чем меньший объем занимает газ, тем меньше становятся межмолекулярные расстояния и тем сильнее возрастает упорядоченность системы. В пределе может произойти конденсация газа с образованием жидкости. Жидкости и твердые тела являются упорядоченными структурами и в отличие от газов практически несжимаемы. Поэтому энтропия конденсированных фаз очень слабо зависит от давления,

В случае, если в ходе процесса изменяются два параметра состояния одновременно, например, газ расширяется и нагревается, переходя из состояния Vj,T] в состояние V₂,T2> то, учитывая независимость изменения энтропии от

пути процесса, результат можно представить как сумму изменений на этапах изохорического нагревания и изотермического расширения или же наоборот;

3.1.3. Изменение энтропии при смешивании идеальных газов (p,T=const)

Типичным примером самопроизвольно протекающего процесса является смешивание газов. Согласно второму началу термодинамики энтропия системы должна при этом возрастать. Убедимся в этом. Представим, что в двух сосудах, соединенных невесомой перегородкой, находятся два невзаимодействующих газа ("1" и "2"). Пусть объемы сосудов и числа молей газов составляют, соответственно, V^niHV^,!^.

3. Критерии (энтропия) 67

Изменение энтропии при смешивании можно представить как сумму двух процессов изотермического расширения

[p# 74]

Так как

то энтропия системы при смешивании должна возрасти. Поскольку:

*

где х, - мольная доля газа "1" в получаемой смеси, то уравнение для изменения энтропии может быть представлено в более удобной форме:

После деления на общее число молей компонентов, образующих смесь ^Гп_; изменение энтропии будет отнесено к одному молю смеси, и в этом случае

Вывод о самопроизвольном возрастании энтропии при смешивании газов равноценен заключению о спонтанном загрязнении веществ при их синтезе.