2.7. Фазовые переходы I рода

Напомним, что фазой называется физически различимая и макроскопически гомогенная часть системы, ограниченная поверхностью раздела, отделяющей её от других гомогенных частей системы.

Каждое чистое вещество может существовать по крайней мере в трех фазовых состояниях: твердом, жидком и газообразном (за исключением гелия для которого кристаллические формы неизвестны). Характерным свойством твёрдого состояния является способность кристаллов существовать в различных модификациях. Это явление для простых веществ получило название аллотропия, а для химических соединений - полиморфизм. Число кристаллических модификаций у индивидуальных веществ зависит от химического состава и для некоторых веществ (например, льда) может быть более десяти. Каждая из модификаций устойчива в определенном интервале температур и давлений.

Понятие фазовые перекода I рода (или первого порядка) объединяет все превращения, которые характеризуются скачкообразным изменением плотности вещества при переходе через температурную границу области устойчивости фазы в условиях постоянства давления или при вариации давления в условиях постоянства температуры.

К таким переходам относятся следующие фазовые превращения:

• кристалл ожидкая фаза (плавление-о-кристаллизация);

• жидкостьопар (парообразование<->конденсация);

• кристаллопар (сублимация(возгонка)-о- десублимация,

2. Энергетика 36

[p# 40]

т.е. кристаллизация из паровой фазы);

" кристалл<->кристалл (полиморфные превращения: а<->р)

При фиксированном внешнем давлении фазовые переходы I рода происходят при постоянной температуре. Они сопровождаются поглощением энергии при нагревании вещества и ее выделением при охлаждении. Соответствующие количества энергии после пересчёта к одному молю вещества называют мольными энтальпиями (теплотами) фазовых превращений.

В условиях постоянства давления теплота превращения равна энтальпии процесса. Изменение внутренней энергии может быть рассчитано по величине энтальпии фазового перехода:

где Аф_л.У - изменение мольного объема, вычисляемое из данных о молярной массе (М) и плотностях (р) сосуществующих фаз:

Энтальпии полиморфных превращений, плавления и парообразования существенно отличаются друг от друга. Для одного и того же вещества энтальпия парообразования, как правило, много больше, чем энтальпия плавления и последняя, в свою очередь, больше, чем энтальпия полиморфного превращения:

2.8. Зависимость теплоёмкости от температуры

Теплоемкость является сложной функцией температуры. Это иллюстрирует рис.2, на котором показаны экспериментальные данные для кристаллов некоторых простых веществ.

2. Энергетика 37

[p# 41]

Рис.2 Данные о низкотемпературной теплоемкости некоторых

Простых веществ

Как видно из рис.2, во всех случаях при Т->0 теплоемкость стремится к нулю. В начале XX века Дебай показал, что в области низких температур теплоемкость кристаллов изменяется пропорционально кубу абсолютной температуры:

где 6д - константа, зависящая от природы вещества.

Эта константа получила название характеристической температуры, Обычно она лежит в пределах 100-400 К. Однако в некоторых случаях величина Эд может быть очень большой. Для алмаза она, например, составляет 1910 К. Большие значения 6_Д характерны для твердых тел с сильным межатомным взаимодействием, что находит отражение в высоких значениях температур плавления веществ и их высокой твердости.

Уравнение Дебая в записанной выше форме используется для аппроксимации экспериментальных данных о теплоемкости в области низких температур или экстраполяции их к абсолютному нулю при температурах ниже 20 К. При более высоких температурах температурная зависимость теплоемкости подчиняется уравнению:

38

[p# 42]

которое также было предложено Дебаем. В этом уравнении:

где h - постоянная Планка; k - константа Больцмана; v - частота колебаний атомных осцилляторов в кристаллической решетке. По Дебаю эта частота может изменяться по определенному закону от v = 0 до v = v_max.

Уравнение Дебая решено в численной форме и представлено в

л /

справочниках*¹ в виде таблицы величин C_v как функции значений % . Таким

образом, индивидуальность веществ согласно Дебаю проявляется только в

значениях характеристической температуры. Иными словами, если представить

данные о низкотемпературных теплоемкостях различных веществ как функцию

% , то все значения должны располагаться на одной и той же кривой. Эта

закономерность действительно наблюдается в случае ряда простых веществ и бинарных соединений (рис. 3).

Рис. 3. Зависимость теплоёмкости некоторых кристаллических веществ (р=1 атм)

от параметра

'^}См., например, [13] в списке рекомендуемой литературы.

[p# 43]

2. Энергетика

39

[p# 44]

Характер зависимости С_р =f(T)_p выше 298 К существенно упрощается и

теплоемкость в большинстве случаев слабо возрастает с повышением температуры. Для неорганических веществ она вполне удовлетворительно описывается степенным полиномом вида:

где константы b и с¹ являются величинами порядка, соответственно, Ю-³ Дж/(моль К²) и 105 д_ж. к/моль.

Для органических веществ используют близкое по форме уравнение:

где с есть величина порядка 10~⁵ Дж/( моль К³).

Следует подчеркнуть, что константа "а" в записанных уравнениях не имеет смысла теплоёмкости при абсолютном нуле, так как оба уравнения справедливы при Т >298 К.

Константы температурной зависимости теплоёмкости экспериментально определены для нескольких тысяч индивидуальных веществ. Их величины приведены в справочных руководствах и базах термодинамических данных.

Если в рассматриваемом температурном интервале вещество претерпевает фазовое превращение I рода, то на кривой температурной зависимости теплоемкости наблюдается разрыв функции.

Количество разрывов при переходе от твердого тела к ненасыщенному пару должно быть не менее двух (плавление, кипение), но при наличии полиморфных превращений число разрывов зависит от того, сколько именно таких превращений происходит при нагревании твердого тела (рис.4). Происхождение разрывов объясняется тем, что в точке превращения, когда разрушается одна молекулярная структура и возникает новая, энергия в форме теплоты подводится к системе, но так как переход I рода осуществляется изотермически, то температура остается неизменной и, следовательно,

производнаяпревращается в бесконечность.

2. Энергетика 40

[p# 45]

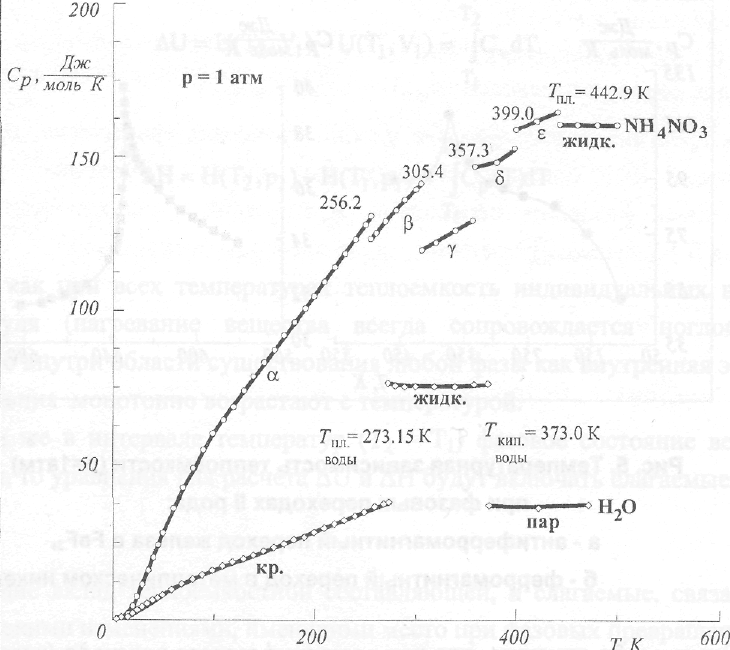
Рис. 4. Температурная зависимость теплоёмкости веществ при наличии фазовых превращений I рода (р=1атм)⁺⁾

Наряду с фазовыми превращениями I рода существуют так называемые фазовые переходы II рода, которые не сопровождаются изменением плотности и возникновением новой фазовой границы. Примерами могут служить магнитные превращения в некоторых кристаллических фазах, а также переходы "проводник-о-сверхпроводник".

Переходы II рода весьма своеобразно проявляются на температурной зависимости теплоемкости. Они происходят в некотором, хотя и достаточно узком интервале температур. С ростом температуры теплоемкость вначале

увеличивается, достигает максимума, резко уменьшается и после завершения превращения вновь начинает монотонно возрастать. Форма кривой С_р =f(T)_p в

области перехода напоминает греческую букву X (лямбда) (рис. 5), что и объясняет происхождение названия "Х-переходы".

''Термодинамические свойства индивидуальных веществ. Отв. ред. В.П. Глушко. 3-е издание-. М.: АН СССР , 1972: тЛ, кн. 2. -328 с : с. 310 (табл. Д.5), с. 321 (табл. Д.22)

2. Энергетика

41

[p# 46]

Рис. 5. Температурная зависимость теплоёмкости (р=1атм)

при фазовых переходах II рода: а - антиферромагнитный переход железа в FeF₃, б - ферромагнитный переход в металлическом никеле.

Стоит особо отметить, что при наличии фазового перехода (независимо от его типа) теплоемкость изменяется не только по абсолютной величине, но и по значениям констант, характеризующих зависимость ее от температуры.