Часть III. Теоретические материалы |
|
Глава 6. Приближенное вычисление интегралов |
|
6.1. Вычисление определенного интеграла |
|
Меню 6.1.4. Примеры квадратурных формул с равноотстоящими узлами |
Вверх Назад Вперёд Пред. След. Указатель Помощь Экран |
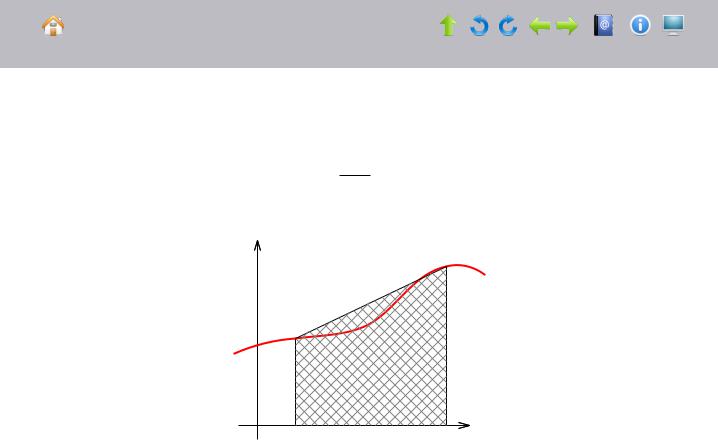
Формула трапеций
Квадратурная формула трапеций (малая) получается как частный случай формулы Ньютона-Котеса (6.9) (или непосредственно) при = 1 и имеет вид
|
≈ 2 |
|
(6.25) |
∫ |
|
||
( ) |
− |
( ( ) + ( )) . |
|
|
|
( )
|
|
Рисунок 6.4
Остаток интерполирования многочленом первой степени при ( ) 2 [ , ] имеет вид
1 ( ) = ( − ) ( − ) |
′′ ( ) |
|
|
. |
|
2 |
||
Часть III. Теоретические материалы |
|
Глава 6. Приближенное вычисление интегралов |
|
6.1. Вычисление определенного интеграла |
|
Меню 6.1.4. Примеры квадратурных формул с равноотстоящими узлами |
Вверх Назад Вперёд Пред. След. Указатель Помощь Экран |
Поэтому (вновь используя факт знакопостоянства одного из сомножителей подынтегральной функции) имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
( ) = |
∫ |
( |
|
) ( |
|
) |
′′ ( ) |
= |
′′ ( ) |
∫ |
( |
|
) ( |
|
) = |
|
( − )3 |
′′ ( ) , |
|
|
[ , ] |
(6.26) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1 |
|
|
− |
|
− |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
− |
|
− |
|
|
|
− |
|
12 |
|
|
|
|
|
|||||||
По аналогии с предыдущими случаями получаем составную формулу трапеций |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
−1 +1 |
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
( ) + ( ) |
−1 |
|
|
|
|
||||||||||||
|
( ) = |
∫ |
|
|
( ) ≈ |
|
|
|
|
|
|
[ ( ) + |
( +1)] = [ |
|
|
|
|
|
|
+ ( )] |
(6.27) |
|||||||||||||||||
|
|
|
2 |
|
=0 |
|
|
|
2 |
|
|
|||||||||||||||||||||||||||
|
∫ |
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
||||
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|||
и ее остаток |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
( − )3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
т |
( ) = |
− |
2 |
′′ ( ) = |
− |
′′ ( ) , |
|
|
[ , ] . |
|
|
|
(6.28) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
12 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пара квадратурных формул трапеций и средних прямоугольников также при определенных условиях (знакопостоянство второй производной интегрируемой функции на отрезке интегрирования) дает двустороннее приближение.
Формула Симпсона
Указанная квадратурная формула получается как частный случай квадратурной формулы НьютонаКотеса при = 2. Таким образом, интерполирование интегрируемой функции ( ) в этом случае осуществляется по трем узлам, равномерно, включая концы, расположенным на отрезке интегрирования:0 = , 1 = +2 , 2 = . По формуле (6.11) при ( ) ≡ 1 (учитывая свойство 1) найдем:
|
|
|
|
|
|
|
1)2−0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
( |
|
∫ |
( |
|
1) ( |
|
2) |
|
1 |
∫ |
( |
|
|
|
|
|
1 |
|
||||||||||||
02 = 22 |
= |
|
|
− |
· |
|
|
|
− |
|
|
− |
|
|
= |
|
2 |
− 3 + 2 = |
|
|
, |
||||||||||||
2 |
|
0 ! |
2 ! |
|
|
|
|
|
|
|
|
4 |
6 |
||||||||||||||||||||
|
|
|
|
|
· |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
) |
|
|
|
|
|
|
|||
|
|
( 1)2−1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
∫ |
|
( |
|
|
1) ( |
|
2) |
|
|
1 |
∫ |
( |
|
|
4 |
|
|
|
|
|||||||||||
12 = |
|
|
− |
· |
|
|
|
|
− |
− |
|
− |
|
|
= − |
|
2 |
− 2 = |
|
|
. |
|
|
|
|||||||||
2 |
|
1 ! |
1 ! |
|
|
|
|
1 |
|
|
|
2 |
6 |
|
|
|
|||||||||||||||||
|
|
|
· |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
) |
|
|
|
|
|
|
||||
Часть III. Теоретические материалы |
|
Глава 6. Приближенное вычисление интегралов |
|
6.1. Вычисление определенного интеграла |
|
Меню 6.1.4. Примеры квадратурных формул с равноотстоящими узлами |
Вверх Назад Вперёд Пред. След. Указатель Помощь Экран |
Следовательно, квадратурная формула Симпсона имеет вид
|
|
|
( |
( |
|
) |
) |
|
∫ |
≈ |
|
|
(6.29) |
||||
6 |
2 |
|||||||
( ) |
− |
( ) + 4 |
|
+ |
|
+ ( ) . |
|
|
Ее алгебраическая степень точности равна 3.
Остаток формулы Симпсона получим, используя замечание 6.1. Остаток многочлена Эрмита в нашем случае имеет вид
2 ( ) = ( − ) ( − |
|
+ |
) |
2 |
(4) ( ) |
|
|
( − ) |
|
, |
|||
|
2 |
4 ! |
если ( ) 4 [ , ]. При этом, очевидно, многочленный сомножитель остатка знакопостоянен. Поэтому интегрирование данного остатка с применением теоремы о среднем дает
|
( − ) ( − |
+ |
) |
2 |
|
(4) |
( ) |
|
|
|
|
(4)( ) |
|
|
|
− ) ( − |
+ |
) |
2 |
|
|
||||||
2С ( ) = ∫ |
|
|
( − ) |
|
|
|
= |
|
|
|
|
∫ |
( |
|
|
( − ) = |
|
||||||||||
2 |
|
4 |
! |
|
4 ! |
|
2 |
|
(6.30) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 (4)( ) |
|
|
( − )5 |
(4) |
|
|
|
|
|
|||||
|
|
|
|
|
|
= − ( |
−2 |
|
) |
|
|
|
|
= − |
|
|
|
( ) . |
|
|
|
||||||
|
|
|
|
|
|
|
90 |
|
|
2880 |
|
|
|
|
|||||||||||||
Составная формула Симпсона в литературе встречается в двух вариантах:
а) отрезок [ , ] разбивается на произвольное количество ( ) частей и на каждой из этих частей интеграл заменяется формулой типа (6.29). В итоге получим квадратурную формулу
|
−1 |
+1 |
|
−1 |
[ ( ) + 4 |
( |
|
+ |
|
) + ( +1)]. |
|
|
∫ |
( ) = =0 |
∫ |
( ) ≈ |
|
|
|
+1 |
(6.31) |
||||
6 =0 |
|
2 |
|
|||||||||
|
∑ |
|
|
|
∑ |
|
|
|
|
|
|
|
Ее остаток по аналогии с рассмотренными выше случаями с использованием формулы (6.30) и имеет
вид
|
С |
( ) = |
− |
4 |
− |
(4) |
( ) = |
− |
( − )5 |
(4) |
( ) , |
|
|
[ , ] . |
(6.32) |
|
2880 4 |
||||||||||||||
|
|
2880 |
|
|
|
|
|
|
|||||||
Часть III. Теоретические материалы |
|
Глава 6. Приближенное вычисление интегралов |
|
6.1. Вычисление определенного интеграла |
|
Меню 6.1.4. Примеры квадратурных формул с равноотстоящими узлами |
Вверх Назад Вперёд Пред. След. Указатель Помощь Экран |
б) Во второй версии отрезок интегрирования разбивается на четное количество (2 ) частей, и интеграл заменяется формулой Симпсона на каждой паре отрезков разбиения (т.е. на отрезке длиной 2 ). Такой вариант составной формулы Симпсона выглядит следующим образом:
|
|
|
|
−1 |
2 +2 |
( ) ≈ |
2 |
−1 |
|
|
||
∫ |
( ) = |
∑ =0 |
∫ 2 |
6 |
∑ =0 |
[ ( 2 ) + 4 ( 2 +1) + ( 2 +2)] = |
|
|||||
|
= |
|
[ ( ) + ( )] + |
4 |
[ ( + ) + ( + 3 ) + · · · + ( − )] + |
(6.33) |
||||||
|
3 |
3 |
|
|||||||||
+23 [ ( + 2 ) + ( + 4 ) + · · · + ( − 2 )] ,
аее остаток примет вид
|
С |
( ) = |
− |
4 |
− |
(4) |
( ) = |
− |
( − )5 |
(4) |
( ) , |
|
|
[ , ] . |
(6.34) |
|
|
180 |
|
|
2880 4 |
|
|
|
|
||||||