
- •Часть I. Руководство пользователя
- •Глава 1. Состав комплекса
- •1.1. Учебные программы
- •1.2. Теоретические материалы
- •1.3. Задачи
- •1.4. Тесты
- •1.5. Демонстрации
- •Глава 2. Интерфейс
- •Часть II. Учебные программы
- •Глава 1. Указатель по специальностям
- •Глава 2. Список программ
- •2.1. Численные методы
- •2.2. Вычислительные методы алгебры
- •2.3. Методы численного анализа - I
- •2.4. Методы численного анализа - II
- •2.5. Численные методы математической физики
- •Часть III. Теоретические материалы
- •Глава 1. Основы машинных вычислений
- •1.1. Машинная арифметика
- •1.1.1. Числа с плавающей точкой
- •1.1.2. Двоичные числа с плавающей точкой
- •1.1.3. Способы округления
- •1.1.4. Расширение множества чисел с плавающей точкой
- •Денормализованные числа
- •Специальные величины
- •Определение машинной арифметики
- •1.1.5. Машинный эпсилон
- •1.1.6. Стандарт IEEE 754
- •1.1.7. Проблемы машинных вычислений
- •1.2. Обусловленность задачи
- •1.2.1. Корректные задачи
- •1.2.2. Векторные нормы
- •1.2.3. Число обусловленности
- •1.2.4. Резюме
- •Глава 2. Методы решения СЛАУ
- •2.1. Обусловленность СЛАУ
- •2.1.1. Матричные нормы
- •2.1.2. Число обусловленности матрицы
- •2.2. Метод Гаусса
- •2.2.1. Базовый метод Гаусса
- •2.2.3. Метод Гаусса с выбором главного элемента
- •2.2.4. Матричные уравнения
- •2.2.5. Обращение матрицы и вычисление определителя
- •2.2.6. Метод прогонки
- •2.3. LU-разложение
- •2.3.2. Выбор главного элемента
- •2.4. Метод квадратного корня
- •2.4.1. Разложение Холецкого
- •2.4.2. Алгоритм метода
- •2.5. Метод отражений
- •2.5.1. Система из двух уравнений
- •2.5.2. Общая схема метода отражений
- •2.6. Метод вращений
- •2.6.1. Система из двух уравнений
- •2.6.2. Общий случай
- •2.7. Методы спуска
- •2.7.1. Метод спуска общего вида
- •2.7.2. Метод градиентного спуска
- •2.7.3. Метод сопряжённых градиентов
- •2.8. Простейшие итерационные методы
- •2.8.1. Принцип сжимающих отображений
- •2.8.2. Общий вид стандартных итерационных методов
- •2.8.3. Критерий сходимости
- •2.8.4. Метод простой итерации
- •2.8.5. Метод Якоби
- •2.8.6. Методы Гаусса–Зейделя и релаксации
- •2.9. Форматы хранения разреженных матриц
- •2.9.1. Координатный формат
- •2.9.2. Форматы CSR и CSC
- •2.9.3. Формат MSR
- •Глава 3. Методы решения проблемы собственных значений
- •3.1. Проблема собственных значений: общая характеристика
- •3.1.1. Сведения из линейной алгебры
- •3.1.2. Общая характеристика проблемы собственных значений
- •3.1.3. Обусловленность проблемы собственных значений
- •3.2. Степенной метод
- •3.2.1. Случай 1
- •3.2.2. Случай 2
- •3.2.3. Случай 3
- •3.2.4. Случай 4
- •3.2.5. Общий случай
- •3.2.6. Степенной метод со сдвигом
- •3.3. Метод вращений Якоби
- •3.3.1. Симметричная проблема собственных значений
- •3.3.2. Общая схема вращений Якоби
- •3.3.3. Расчётные формулы метода
- •3.4. Метод Данилевского
- •Глава 4. Решение численных уравнений
- •4.1. Приближенное решение одного численного уравнения
- •4.1.1. Введение
- •4.1.2. Метод бисекции
- •4.1.3. Метод простой итерации решения численных уравнений
- •4.1.4. О задаче улучшения метода итерации
- •Метод Стеффенсена
- •Улучшение итерационного процесса при помощи преобразования заданного уравнения
- •4.1.5. Метод Ньютона
- •4.1.6. Видоизменения метода Ньютона
- •Случай кратных корней
- •Упрощение вычислений
- •Дискретный вариант метода Ньютона
- •Метод секущих
- •Метод хорд и комбинированные методы
- •4.1.7. Методы отыскания корней алгебраических уравнений
- •Метод Лобачевского
- •Метод Лина разложения многочлена на множители
- •Метод Лина выделения линейного множителя
- •4.2. Приближенное решение систем численных уравнений
- •4.2.1. Метод простой итерации и его видоизменения
- •Методы Зейделя и Гаусса-Зейделя
- •4.2.2. Метод Ньютона и его видоизменения
- •4.2.3. Другие подходы к решению нелинейных систем
- •Методы вариационного типа
- •Методы продолжения по параметру
- •Глава 5. Приближение функций
- •5.1. Общая информация
- •5.2. Наилучшие приближения функций
- •5.2.1. Введение
- •5.2.2. Наилучшие приближения в гильбертовом пространстве
- •Наилучшее среднеквадратичное приближение функций алгебраическими многочленами
- •Метод наименьших квадратов
- •5.2.3. Наилучшее равномерное приближение
- •Многочлен наилучшего равномерного приближения
- •Примеры наилучшего равномерного приближения
- •5.3. Интерполирование
- •5.3.1. Введение
- •5.3.2. Задача интерполирования по значениям функции
- •5.3.3. Представления алгебраического интерполяционного многочлена
- •Представление алгебраического интерполяционного многочлена в форме Лагранжа
- •Разделенные разности и их свойства
- •Представление алгебраического интерполяционного многочлена в форме Ньютона
- •5.3.4. Остаток интерполирования
- •Остаточный член в форме Ньютона
- •Остаточный член в форме Лагранжа
- •5.3.5. Минимизация остатка интерполирования
- •5.3.6. Интерполирование при равноотстоящих узлах
- •Конечные разности
- •5.3.7. Некоторые правила интерполирования
- •Интерполирование в начале таблицы
- •Интерполирование в конце таблицы
- •Интерполирование внутри таблицы
- •5.3.8. Интерполирование с кратными узлами
- •Остаточный член интерполяционной формулы Эрмита
- •Частные случаи интерполирования Эрмита
- •5.3.9. Сходимость интерполяционного процесса
- •5.3.10. Некоторые приложения интерполирования
- •Приближенное вычисление производных
- •Применение интерполирования к решению уравнений
- •5.3.11. Многомерная алгебраическая интерполяция
- •Интерполяционный многочлен первой степени
- •Обобщение интерполяционных формул Ньютона на случай функций многих переменных
- •Последовательная интерполяция на прямоугольной сетке
- •Общий случай интерполирования на треугольнике
- •5.4. Приближение сплайнами
- •5.4.1. Общее определение сплайна. Простейшие примеры
- •Интерполяционный сплайн первой степени
- •5.4.2. Интерполяционный кубический сплайн
- •Сходимость процесса интерполирования кубическими сплайнами
- •5.4.3. Кусочно-кубическая интерполяция со сглаживанием
- •5.4.4. Интерполяционный бикубический сплайн
- •5.4.5. Приближение кривых и поверхностей
- •Интерполяция кривых сплайнами
- •Глава 6. Приближенное вычисление интегралов
- •6.1. Вычисление определенного интеграла
- •6.1.1. Задача численного интегрирования
- •6.1.2. Интерполяционные квадратурные формулы
- •6.1.3. Квадратурные формулы Ньютона–Котеса
- •6.1.4. Примеры квадратурных формул с равноотстоящими узлами
- •Квадратурные формулы с одним узлом
- •Формула трапеций
- •Формула Симпсона
- •6.1.5. Оценка погрешности квадратурных формул
- •Учет избыточной гладкости интегрируемой функции
- •Правило Рунге
- •6.1.6. Квадратурные формулы Гаусса
- •Тождество Кристоффеля–Дарбу
- •Остаток квадратурных формул типа Гаусса
- •Некоторые частные случаи квадратурных формул типа Гаусса
- •6.1.7. Квадратурные формулы, содержащие наперед заданные узлы
- •Формулы с предписанными узлами частного вида (формулы типа Маркова)
- •6.1.8. Квадратурные формулы с равными коэффициентами
- •6.1.9. Нестандартные приемы интегрирования
- •Метод Филона
- •Повышение гладкости интегрируемой функции
- •Случай бесконечных пределов интегрирования
- •6.2. Вычисление кратных интегралов
- •6.2.1. Cведении кратного интеграла к повторному
- •Повторное интегрирование по прямоугольной области
- •Интегралы по криволинейной трапеции
- •6.2.2. Простейшие кубатурные формулы
- •Кубатурные формулы на прямоугольнике
- •Кубатурные формулы на треугольнике
- •Глава 7. Численное решение интегральных уравнений
- •7.1. Введение
- •7.2.1. Метод механических квадратур
- •Оценка погрешности метода механических квадратур
- •7.2.2. Метод замены ядра на вырожденное
- •Разложение ядра в ряд Тейлора
- •Использование ортогональных разложений
- •Интерполяционные способы замены ядра
- •Способ Бэтмена
- •7.2.3. Метод последовательных приближений
- •7.2.4. Решение интегральных уравнений Вольтерра 2-го рода
- •Метод механических квадратур
- •Метод последовательных приближений
- •7.3. Проекционные методы решения интегральных уравнений
- •7.3.1. Метод моментов и метод Галеркина
- •Связь метода Галеркина с заменой ядра вырожденным
- •7.3.2. Другие проекционные методы
- •Метод наименьших квадратов
- •Метод коллокации
- •7.4. Решение интегральных уравнений первого рода
- •7.4.1. Основные определения и примеры
- •7.4.2. Метод регуляризации решения некорректных задач
- •Вариационный метод регуляризации
- •Выбор параметров регуляризации
- •Уравнение Эйлера
- •Замечание о решении плохо обусловленных линейных систем
- •Глава 8. Методы решения задачи Коши для ОДУ
- •8.1. Общая информация
- •8.1.1. Введение
- •8.1.2. Классификация методов решения задачи Коши
- •8.2. Одношаговые методы решения задачи Коши
- •8.2.1. Пошаговый вариант метода рядов
- •8.2.2. Способ Рунге–Кутта построения одношаговых методов
- •8.2.3. Явные методы Рунге–Кутта
- •Методы первого порядка точности
- •Методы второго порядка точности
- •Методы третьего и четвертого порядка точности
- •8.2.4. Способ последовательного повышения порядка точности
- •Методы первого порядка точности
- •Методы второго порядка точности
- •Методы третьего порядка точности
- •8.2.5. Практический контроль погрешности приближенного решения
- •Правило Рунге
- •Использование вложенных методов
- •8.2.6. Сходимость одношаговых методов решения задачи Коши
- •8.3. Многошаговые методы решения задачи Коши
- •8.3.1. Введение
- •8.3.2. Методы Адамса
- •Экстраполяционные методы Адамса
- •Интерполяционные методы Адамса
- •8.3.3. Общие линейные многошаговые методы
- •8.4. Понятие устойчивости численных методов решения задачи Коши
- •8.4.1. Корневое условие
- •8.4.2. Устойчивость на модельном уравнении
- •8.5. Жесткие задачи и методы их решения
- •8.5.1. Явление жесткости
- •8.5.2. Методы, применяемые для решения жестких систем
- •Неявные методы Рунге–Кутта
- •Формулы дифференцирования назад
- •Реализация неявных методов
- •Глава 9. Методы решения граничных задач для ОДУ
- •9.1. Введение
- •9.2. Методы, основанные на сведении к решению задач Коши
- •9.2.1. Метод редукции граничных задач к задачам Коши
- •9.2.2. Метод стрельбы для линейных граничных задач
- •Уравнение второго порядка случай
- •Общий линейный случай
- •9.2.3. Метод дифференциальной прогонки
- •9.2.4. Метод стрельбы для нелинейных граничных задач
- •9.3. Проекционные методы решения граничных задач
- •9.3.1. Введение
- •9.3.2. Вариационные методы решения граничных задач
- •Вариационная задача для операторных уравнений
- •Граничная задача для обыкновенного дифференциального уравнения второго порядка как операторное уравнение
- •Метод Ритца нахождения минимума функционала
- •Сходимость минимизирующей последовательности к минимизирующей функции
- •Построение минимизирующей последовательности по Ритцу
- •9.3.3. Метод моментов и метод Галеркина решения граничных задач
- •9.3.4. Метод наименьших квадратов решения граничных задач
- •9.3.5. Метод коллокации решения граничных задач
- •Глава 10. Численные методы математической физики
- •10.1. Основные понятия теории разностных схем
- •10.1.1. Сетки
- •Равномерная сетка на отрезке
- •Неравномерная сетка на отрезке
- •Сетка в прямоугольнике
- •Сетка в криволинейной ортогональной системе координат
- •Пространственно-временная сетка в прямоугольнике
- •Прямоугольная сетка в области сложной формы
- •Треугольная сетка в области сложной формы
- •Сетка на криволинейном четырехугольнике
- •10.1.2. Cеточные функции
- •10.1.3. Разностная аппроксимация дифференциальных операторов
- •Способ неопределенных коэффициентов
- •Способ численного дифференцирования
- •10.1.4. Погрешность аппроксимации на сетке
- •10.1.5. Постановка разностной задачи
- •10.1.6. Сходимость и точность разностных схем
- •10.1.7. Повышение порядка аппроксимации разностных схем
- •10.1.8. Математический аппарат теории разностных схем
- •Некоторые разностные формулы
- •Отыскание собственных функций и собственных значений на примере простейшей разностной задачи
- •Разностные аналоги теорем вложения
- •Метод энергетических неравенств
- •10.2. Способы построения разностных схем
- •10.2.1. Требования, предъявляемые к разностным схемам
- •Однородные разностные схемы
- •Консервативные разностные схемы
- •Аппроксимация и сходимость построенной разностной схемы
- •Метод Ритца построения разностных схем
- •Метод аппроксимации квадратичного функционала
- •Метод Галеркина построения разностных схем
- •Метод аппроксимации интегрального тождества
- •10.3. Методы исследования устойчивости разностных схем
- •10.3.1. Принцип максимума
- •Примеры исследования устойчивости с помощью принципа максимума
- •Монотонные разностные схемы для обыкновенных дифференциальных уравнений второго порядка
- •10.3.2. Метод разделения переменных
- •10.3.3. Метод энергетических неравенств
- •10.4.1. Задача Дирихле в прямоугольнике
- •10.4.2. Консервативная схема для задачи Дирихле
- •10.5. Итерационные методы решения разностных задач
- •10.5.1. Двухслойные итерационные схемы
- •10.5.2. Свойства разностного оператора Лапласа
- •10.5.3. Метод простых итераций
- •10.5.4. Методы Зейделя и релаксации
- •10.6.1. Метод замены переменных
- •10.6.2. Разностный метод
- •10.6.3. Метод конечных элементов
- •Триангуляция области и базисные пирамидальные функции
- •МКЭ на основе метода Галеркина
- •Интегро-интерполяционный метод конечных элементов
- •10.6.4. Метод граничных элементов
- •Первая аппроксимация
- •Вторая аппроксимация
- •Предметный указатель
- •Другие
- •Определения
- •Cтрого нормированное пространство
- •А-устойчивость
- •Абсолютная и относительная погрешности округления
- •Адаптивная сетка
- •Алгебраическая степень точности квадратурной формулы
- •Базисные пирамидальные функции
- •Внутренние узлы
- •Вырожденное ядро интегрального оператора
- •Градиент
- •Граничные узлы
- •Двухслойная итерационная схема
- •Денормализованное число с плавающей точкой
- •Диагонализируемая матрица
- •Диагональное преобладание
- •Жесткая система ОДУ
- •Интерполяционная квадратурная формула
- •Консервативная разностная схема
- •Корневое условие
- •Корректно поставленная задача
- •Круг Гершгорина
- •Линейная аппроксимация
- •Локальная погрешность метода
- •Машинная арифметика с плавающей точкой
- •Машинные числа
- •Машинный эпсилон
- •Метод верхней релаксации
- •Многочлен наилучшего равномерного приближения
- •Наилучшее приближение
- •Норма Фробениуса
- •Норма линейного оператора
- •Нормализованное число с плавающей точкой
- •Нормальная матрица
- •Носитель функции
- •Область устойчивости метода решения задачи Коши
- •Область устойчивости метода решения задачи Коши
- •Пирамидальная функция
- •Погрешность аппроксимации
- •Полиномиальный бикубический сплайн
- •Полиномиальный сплайн
- •Полная в классе система
- •Положительно определенная матрица
- •Положительно определенный оператор
- •Правило округления
- •Разреженная матрица
- •Регуляризирующий оператор
- •Самосопряженный оператор
- •Сетка
- •Сжимающее отображение
- •Система функций Чебышева
- •Собственные значения и собственные векторы
- •Спектральный радиус
- •Степень точности квадратурной формулы
- •Триангуляция области
- •Устойчивость метода решения задачи Коши
- •Фундаментальная последовательность
- •Фундаментальное решение уравнения Лапласа
- •Число обусловленности задачи
- •Число обусловленности матрицы
- •Число с плавающей точкой
- •Элемент наилучшего приближения
- •Доказательства теорем
- •Часть IV. Задачи
- •Глава 1. Машинная арифметика
- •Глава 2. Решение систем линейных алгебраических уравнений
- •2.1. Метод Гаусса
- •2.2. LU-разложение
- •2.3. Метод квадратного корня
- •2.4. Методы ортогональных преобразований
- •2.5. Итерационные методы
- •Глава 3. Решение численных уравнений
- •3.1. Метод бисекции
- •3.2. Метод Ньютона
- •Глава 4. Интерполяция
- •4.1. Понятие интерполяции
- •4.2. Интерполяционный многочлен в форме Лагранжа
- •4.3. Интерполяционный многочлен в форме Ньютона
- •Глава 5. Численное интегрирование
- •5.1. Простейшие квадратурные формулы
- •5.2. Квадратурные формулы НАСТ
- •5.3. Практическая оценка погрешности
- •Глава 6. Численные методы математической физики
- •6.1. Аппроксимация дифференциальных задач разностными схемами
- •6.2. Исследование устойчивости разностных схем
- •6.3. Реализация разностных схем для уравнений теплопроводности и колебаний струны
- •Решения и указания
- •Ответы к задачам
- •Часть V. Тесты
- •Тест 1. Методы решения СЛАУ
- •1.1. Число обусловленности. Прямые методы решения СЛАУ
- •Тест 2. Решение нелинейных уравнений
- •Тест 3. Приближение функций
- •Тест 4. Численное интегрирование
- •Тест 5. Дифференциальные уравнения
- •Рекомендуемая литература

Часть III. Теоретические материалы Глава 2. Методы решения СЛАУ 2.5. Метод отражений
Меню |
Вверх Назад Вперёд Пред. След. Указатель Помощь Экран |
2.5. Метод отражений
2.5.1.Система из двух уравнений
2.5.2.Общая схема метода отражений
2.5.3.-разложение
Недостатком метода Гаусса и его модификаций является то, что элементарные преобразования в общем случае ухудшают обусловленность исходной системы (æ∞( ) > 1). Поэтому разработаны альтернативные методы приведения матрицы к треугольному виду, основанные на ортогональных преобразованиях.
Часть III. Теоретические материалы Глава 2. Методы решения СЛАУ 2.5. Метод отражений
Меню 2.5.1. Система из двух уравнений Вверх Назад Вперёд Пред. След. Указатель Помощь Экран
2.5.1. Система из двух уравнений
Рассмотрим СЛАУ |
[ 21 |
|
][ 2 |
] |
|
[ 2 |
]. |
|
= |
22 |
= |
(2.33) |
|||||
|
11 |
12 |
1 |
|
|
1 |
|
|
Для её решения применим к обеим частям ортогональное линейное преобразование , которое «обнуляет» элемент 21:
= ′ = [ |
0 |
22′ |
][ 2 |
] |
= |
[ 2′ |
] |
= . |
(5.1′) |
|
11′ |
12′ |
1 |
|
|
1′ |
|
|
|
Пусть — -й столбец матрицы , тогда ′ = . Так как ортогональные преобразования сохраняют евклидову норму векторов, имеем ‖ ‖ = ‖ ′‖ (в дальнейшем ‖ · ‖ = ‖ · ‖2), поэтому 11′ = ±‖ 1‖.
|
|
|
− ′ |
|
′ |
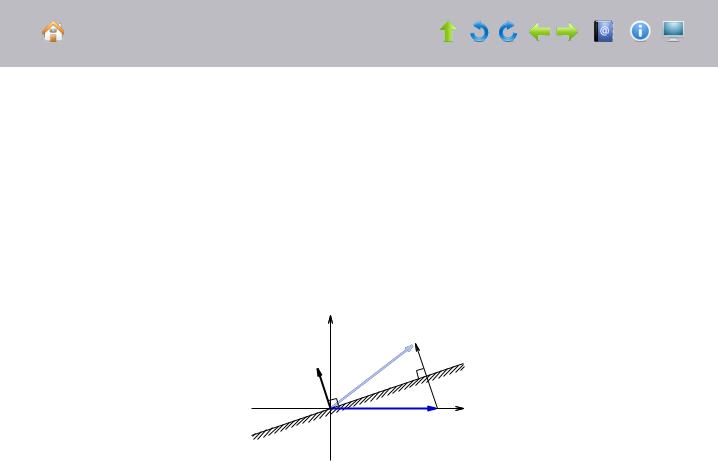
Рисунок 2.2 Преобразование отражения на плоскости. |
|
Рассмотрим вектор = 1, под действием переходящий в ′ = 1′ . Наша задача — определить как преобразование отражения относительно какой-то гиперплоскости, что равносильно нахождению вектора нормали к этой гиперплоскости, ‖ ‖ = 1. Нетрудно заметить, что векторы − ′ и коллинеарны, следовательно

Часть III. Теоретические материалы Глава 2. Методы решения СЛАУ 2.5. Метод отражений
Меню 2.5.1. Система из двух уравнений |
|
|
|
|
|
|
|
Вверх |
Назад |
Вперёд Пред. След. |
Указатель Помощь Экран |
= ± |
|
|
|
− |
′ |
. |
|
|
(2.34) |
||
|
|
|
|
′‖ |
|
|
|||||
‖ |
− |
|
|
||||||||
|
|
|
|
|
|
найти ′. Из |
|
||||
Теперь рассмотрим обратную задачу: по данным |
векторам и |
|
(2.34) имеем |
||||||||
±‖ − ′‖ = − ′ ′ = − , R.Так как ( + ′) , ( + ′, ) = (2 − , ) = 0 |
= 2( , ), |
||||||||||
откуда в итоге получаем |
|
|
2( , ) . |
|
|
|
|||||
′ = |
− |
|
|
(2.35) |
|||||||
|
|
|
|
|
|
|
|
|
|||
Таким образом, в случае системы (2.33) прямой ход метода отражений состоит в следующем:
1)По формуле (2.34) найти вектор нормали , определяющий гиперплоскость, при отражении относительно которой вектор 1 переходит в 1′ = (±‖ 1‖, 0) .
2)По формуле (2.35) применить найденное преобразование отражения к векторам 2 и .

Часть III. Теоретические материалы Глава 2. Методы решения СЛАУ 2.5. Метод отражений
Меню 2.5.2. Общая схема метода отражений Вверх Назад Вперёд Пред. След. Указатель Помощь Экран
2.5.2. Общая схема метода отражений
В случае СЛАУ произвольной размерности, метод отражений, как и в двумерном случае, определяется формулами (2.34), (2.35). Алгоритм метода имеет следующий вид (напомним, что обозначает -й векторстолбец матрицы ).
1) Вычислить по формуле (2.34), где = 1, ′ = 1′ = (±‖ 1‖, 0, . . . , 0) .
2) |
1 ← |
1 |
← |
|
̸ |
← |
′ по формуле (2.35). |
|
′ ; вычислить |
′ |
|
= 1, |
|
3)Повторить шаги 1-2 для нижней правой подматрицы и соответствующего подвектора размерности− 1, и так далее до тех пор, пока матрица не станет верхнетреугольной.
Замечание 2.6. При реализации метода отражений существует свобода выбора знака для вектора 1′ . Чтобы избежать вычитания близких чисел при вычислении по формуле (2.34), этот знак выбирают таким образом, чтобы он был противоположен знаку 11 ( в общем случае). Тогда при вычислении 1 − 1′ фактически будут складываться два одинаковых по модулю числа.

Часть III. Теоретические материалы Глава 2. Методы решения СЛАУ 2.5. Метод отражений
Меню 2.5.3. -разложение Вверх Назад Вперёд Пред. След. Указатель Помощь Экран
2.5.3. -разложение
Найдём в явном виде матрицу преобразования отражения, задаваемого формулой (2.35).
′ = − 2( , ) = − 2 ( ) = − 2( ) = ( − 2 ) .
Определение. Пусть R (C ), ‖ ‖2 = 1. Матрица
= ( ) = − 2
называется матрицей отражения. Она задаёт преобразование отражения относительно гиперплоскости с нормалью .
Свойства матрицы отражения
1.( ) = ( )−1.
2.Матрица отражения является симметричной (самосопряжённой).
3.Матрица отражения является ортогональной (унитарной).
4.Все собственные значения матрицы отражения равны ±1.
Доказательство. Так как матрица унитарна, имеем ‖ ‖ = 1. Пусть — произвольное собственное значение , — соответствующий собственный вектор: = . Тогда ‖ ‖ = ‖ ‖ = ‖ ‖, откуда | | = 1.
Докажем теперь, что собственные числа самосопряжённой матрицы вещественны:
= * ( , ) = ( , * ) = ( , ) = ( , ) ( , ) R C .
Далее пусть — собственный вектор. Тогда
( , ) = ( , ) = ‖ ‖2 = ( , ) R.
Таким образом, | | = 1 и R, то есть = ±1.

Часть III. Теоретические материалы Глава 2. Методы решения СЛАУ 2.5. Метод отражений
Меню 2.5.3. -разложение Вверх Назад Вперёд Пред. След. Указатель Помощь Экран
Замечание 2.7. Заметим, что вычисление преобразования отражения по формуле (2.35) требует ( ) операций умножения и сложения, в то время как умножение на матрицу ( ) требует ( 2) операций. Поэтому в явном виде ( ) практически никогда не используют, а хранят только .
Процесс преобразования к верхнетреугольному виду по методу отражений можно представить в виде
|
( +1) = ( ), |
|
|
|
|
|||
где — блочная матрица вида |
= [ |
|
( )] |
|
|
|
|
|
|
0 |
, |
|
|
(2.36) |
|||
|
|
−1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 — единичная матрица размерности − 1, |
— вектор нормали размерности − + 1. |
|
||||||
Таким образом мы имеем |
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
( ) |
, |
|
|
−1 . . . 2 1 = = |
|
|
||||||
откуда |
|
|
|
|
|
|
|
|
= , |
где = ˜−1, |
= ( ). |
(2.37) |
|||||
Определение. -разложением матрицы называется её представление в виде
= ,
где — ортогональная ( −1 = ), а — верхнетреугольная матрица.
Теорема 2.7 (о -разложении). Для любой вещественной квадратной матрицы существует - разложение: = , где — ортогональная, — верхнетреугольная матрица с неотрицательными диагональными элементами. Если det ̸= 0, то все диагональные элементы положительны. [Доказательство]
Рассмотрим подробно алгоритм построения -разложения методом отражений. Из (2.37) имеем
= ˜−1 = ( |
−1 |
. . . )−1 |
= |
1 |
. . . |
, |
|
1 |
|
−1 |
|
где определяются формулой (2.36) (здесь мы использовали тот факт, что −1 = ).

Часть III. Теоретические материалы Глава 2. Методы решения СЛАУ 2.5. Метод отражений
Меню 2.5.3. -разложение Вверх Назад Вперёд Пред. След. Указатель Помощь Экран
Cогласно замечанию 2.7 вместо того, чтобы хранить отдельно матрицу , мы можем хранить лишь векторы , которые однозначно определяют . Кроме того, так как R − +1, можно их хранить на месте нижнего треугольника матрицы (для этого необходимо завести отдельный вектор для хранения диагональных элементов ).
Предположим, что нам известно -разложение матрицы . Тогда решение СЛАУ = осуществляется за ( 2) операций:
= |
|
{ |
= . |
|
|
|
= , |
Таким образом, сначала вычисляется = −1 = , а затем обратной подстановкой находится . Если матрица хранится в виде набора нормалей , то вычисление вектора
= −1 = −1 . . . 1
эквивалентно последовательному применению к вектору всех преобразований отражения, использованных при построении -разложения.
