Тема 2. Лебеговское продолжение меры. Мера в Rn

Пусть задано множество X и – полукольцо его подмножеств, на котором задана мера m. Мера , заданная на кольце K называется продолжением меры m, если и для всех выполняется .

Теорема. Пусть – мера на полукольце и K(S) – минимальное кольцо, порожденное S. Тогда на K(S) существует единственная мера , являющаяся продолжением меры m. Если мера m на полукольце является -аддитивной, то её продолжение также -аддитивная мера.

Пусть – алгебра подмножеств множества X, m – -аддитивная мера на K. Внешней мерой множества называется число

где нижняя грань берётся по всевозможным конечным или счётным покрытиям множества A элементарными множествами.

Свойства внешней меры заданной на кольце:

1. если , то

2. для всех , и

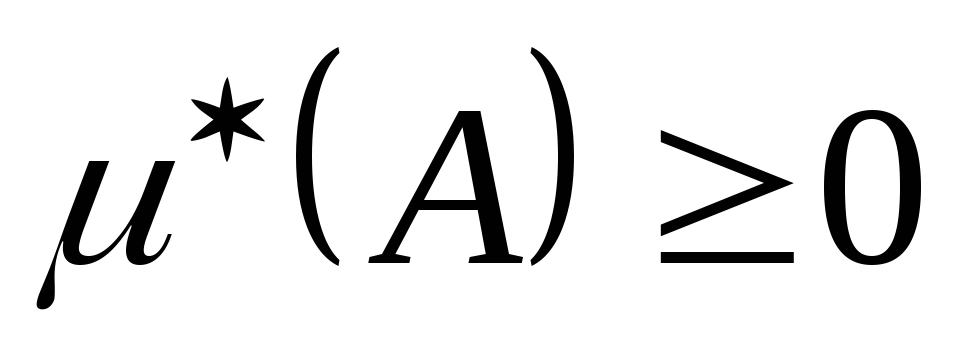3. для всех и выполняется

4. внешняя мера счётно-полуаддитивна, т.е. для всех имеет место неравенство:

5. для всех

Внутренней мерой множества называется число .

Для всех имеет место неравенство:

Пусть m – полная, счётно-аддитивная, конечная мера. Множество называется измеримым по Лебегу относительно меры m, заданной на алгебре множеств К, если выполняется равенство:

Для измеримого по Лебегу множества определим меру Совокупность измеримых множеств обозначим .

Теорема 1 (критерий измеримости множества). Пусть задано пространство (X, , m). Тогда для всех следующие утверждения эквивалентны:

1. А измеримо по Лебегу относительно меры m;

2. для любого что

Следствие. Множество измеримо, если для всех существует измеримое множество B такое, что

Теорема 2. (о -алгебре измеримых множеств). Совокупность  измеримых множеств образует -алгебру множеств, содержащую исходную алгебру K. Сужение  внешней меры ^* на измеримые множества является мерой на .

Следствие. Счётное пересечение измеримых множеств измеримо.

Мера m, заданная на алгебре K, называется полной, если из и следует, что и

Одним из важнейших примеров меры является мера Лебега на числовой прямой.

Пусть – некоторый фиксированный полуинтервал прямой, – полукольцо, состоящее из полуинтервалов . Пусть K – алгебра подмножеств, порождённая полукольцом S, каждый элемент которой имеет вид причём полуинтервалы в правой части попарно не пересекаются. Через m обозначим меру на алгебре K, полученную продолжением меры с полукольца, т.е. . Для произвольного множества определим внешнюю меру , где точная нижняя грань берётся по всем таким наборам полуинтервалов , что . Множество называется измеримым по Лебегу, если Таким образом, мерой Лебега  на отрезке называется лебеговское продолжение длины.

Рассмотрим измеримые по Лебегу линейные ограниченные множества:

1. множество, состоящее из одной точки, измеримо и его мера равна нулю;

2. всякое не более чем счётное ограниченное множество точек прямой измеримо и его мера равна нулю;

3. любой промежуток измерим и его мера равна его длине;

4. любое ограниченное открытое или замкнутое множество измеримо по Лебегу;

5. любое ограниченное борелевское множество на прямой измеримо по Лебегу.

Часто приходится рассматривать меры, которые могут принимать и бесконечные значения. Ограничимся случаем - конечных мер.

Мера , принимающая бесконечные значения, называется - конечной, если существует последовательность множеств такая, что , для всех i и .

Можно показать, что если мера , заданная на алгебре K подмножеств X, -конечна, то X можно представить в виде объединения счётной системы попарно непересекающихся множеств конечной меры.

Рассмотрим теорию измеримости по Лебегу для произвольных (даже неограниченных) множеств на прямой. Длина как мера на R является -аддитивной, потому что . Множество называется измеримым по Лебегу, если для всех измеримо по Лебегу ограниченное множество или .

Совокупность всех измеримых подмножеств R обозначим . Обозначим через . Тогда и . Если ряд расходится, то .

Утверждение 1. Совокупность  всех измеримых по Лебегу подмножеств R является -алгеброй.

Утверждение 2. Введённая функция является -конечной мерой на -алгебре  всех измеримых множеств на R.

Пусть задана неубывающая функция , т.е. .

Скачком функции F в точке называется число , где соответственно правосторонний предел и левосторонний предел в точке x. На концах отрезка: , .

Скачок неубывающей функции в любой точке неотрицателен, причём функция F непрерывна в точке x тогда и только тогда, когда .