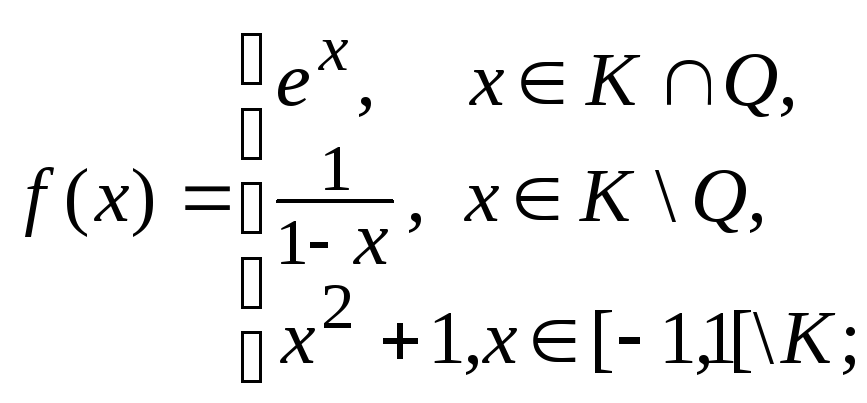Тема 3. ИЗМЕРИМЫЕ ФУНКЦИИ. СХОДИМОСТЬ НА ПРОСТРАНСТВЕ С МЕРОЙ

Множество X, на котором задана некоторая -алгебра его подмножеств  и задана мера  называется пространством с мерой и обозначается (X, , ). Будем предполагать, что  – -аддитивная полная мера.

В дальнейшем будем изучать числовые функции, заданные на измеримом пространстве X.

Функция f : XR называется измеримой, если для любых c  R множество A_c = {x : f (x) < c} измеримо, т.е. A_c  .

Теорема 1. Числовая функция f, заданная на измеримом пространстве (X, ) измерима тогда и только тогда, когда для всех cR одно из множеств {x : f (x)  c}, {x : f (x) > c}, {x : f (x)  c} измеримо.

На числовой прямой измеримой является любая непрерывная функция, а также функция Дирихле

Пусть _A(x) – характеристическая функция множества A, т.е. _A(x)=1, если xA и _A(x)=0, если xA. Функция _A(x) измерима, если измеримо множество A.

Обозначим через S(X) множество всех измеримых числовых функций f : X  R, заданных на измеримом пространстве (X, ).

Теорема 2. Пусть f : X  R – измеримая функция. Тогда для любой измеримой функции g : R  R их композиция h = gf также измерима на X.

Теорема 3. Пусть f, gS(X),  = const. Тогда следующие функции измеримы на X : f, f², f+g, fg, fg (при условии, что g(x)0 на X).

Одним из свойств пространства S(X) является его замкнутость относительно предельного перехода. Мы будем рассматривать четыре типа сходимости.

1. Точечная сходимость.

Последовательность f_n сходится к функции f поточечно, если для всех xX f_n(x)f(x) при n.

2. Равномерная сходимость.

Последовательность функций f_n сходится к f равномерно, если для любого  > 0 существует n_ такой, что при n>n_ |f_n(x) –f(x)| <  для всех xX.

3. Сходимость почти всюду.

Последовательность f_n сходится к f, если f_n(x)f(x) при n для всех xX за исключением множества меры нуль.

4. Сходимость по мере.

Говорят, что последовательность конечных измеримых функций f_n сходится по мере к измеримой функции f, если для всякого числа  > 0

Очевидно, что из равномерной сходимости следует сходимость точечная, а из точечной – сходимость почти всюду.

Теорема 4. Пусть последовательность f_n(x) измеримых функций для всех xX сходится к функции f. Тогда и функция f измерима.

Следствие 1. Если , f_k(x)S(X) сходится к f равномерно, то f(x)S(X).

Следствие 2. Если , f_k(x)S(X) сходится к f почти всюду, то f(x)S(X).

Следствие 3. Существует разрывная на отрезке [a;b] функция, которая не является пределом почти всюду сходящейся последовательности непрерывных функций.

В качестве такой функции можно взять неизмеримую функцию.

Теорема 5 (Лебега). Пусть последовательность конечных измеримых функций сходится к измеримой функции f почти всюду. Тогда она сходится и по мере.

Теорема 6 (Рисса). Пусть последовательность конечных измеримых функций сходится к измеримой функции f по мере. Тогда из этой последовательности можно выделить подпоследовательность , сходящуюся почти всюду.

Пусть задано пространство (X, , ) с конечной мерой. Говорят, что некоторое свойство выполнено почти всюду, если оно выполнено на XA, а (A)=0.

Будем рассматривать числовые функции, которые почти всюду конечны.

Две функции f и g называются эквивалентными, если они совпадают почти всюду, т.е. {x: fg}=0.

Теорема 7. Пусть f  S(X) и f  g, тогда g S(X).

Теорема 8 (Егорова). Пусть X – пространство с конечной мерой и последовательность измеримых функций сходится почти всюду на X к измеримой функции f. Тогда для любого  >0 найдётся такое измеримое множество X_ X, что:

1. (X\X_)<;

2. на X_ последовательность 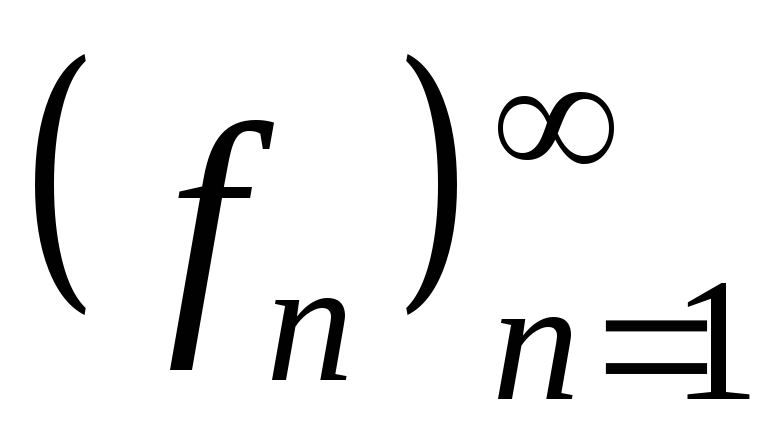сходится к f равномерно.

Теорема 9 (Лузина). Пусть X  R – измеримое по Лебегу множество конечной меры и пусть f : X R измерима и почти всюду конечна. Тогда для всех  > 0 существует F_  X – замкнутое множество, что функция f на F_ непрерывна и  (X\F_) <.

Примеры решения задач

Задача 1. Пусть – последовательность измеримых на X функций. Тогда , измеримы на X.

Решение. Обозначим через h(x) = . Измеримость h(x) означает, что для  c  R измеримы множества . Покажем, что =, что и будет означать измеримость h. Пусть , т.е. h(x)>c. Тогда h(x)>c+ при достаточно малом  > 0. По определению точной верхней границы найдётся такой номер n₀, что >h(x)–. Отсюда >(c+)-=с и потому , а тем более, .

С другой стороны, пусть . Это значит, что найдётся такой номер n₀, что > c. Но тогда h (x)  > c, т.е. . Равенство доказано. Аналогично доказывается измеримость .

Задача 2. Определим функцию f(x) на [0,1] следующим образом. Если x = 0,n₁n₂… – десятичная запись числа x, то .

Решение. Рассмотрим множество чисел отрезка [0,1], в десятичной записи которых присутствует цифра 9. Мера данного множества равна . Следовательно, функция f(x) равна 9 почти всюду. Функция f(x) измерима как постоянная функция.

Задача 3. Доказать, что функция f измерима тогда и только тогда, когда измерима функция sin f.

Решение. Обозначим через g(x) = sin x, тогда при измеримости функции f имеем h(x) = g(f(x)) = sin f – композиция непрерывной и измеримой и поэтому sin f будет измеримой. С другой стороны, пусть измерима функция h(x) = sin f(x), покажем, что измерима функция f(x). Измеримость sin f означает, что для с  R измеримо множество {f(x):sinf(x)>c} =

Таким образом, измеримыми являются пустое множество, числовая прямая и для c  R множество , arccos c [0,].

Задача 4. Доказать, что функция y = f(x), x  R измерима на R, если 1) f(x) = sin[x]; 2) f(x)=.

Решение. 1) Функция f(x) принимает счётное число значений sink, kZ. А именно, , если x  A_k = [k, k+1[ и =R. Так как промежутки A_k являются измеримыми, то f(x) является простой функцией и, следовательно, измеримой.

2) Члены рассматриваемого ряда являются непрерывными функциями и поэтому измеримы. Если x 0, то эквивалентность при n позволяет сделать вывод о равномерной сходимости этого функционального ряда для x  0. Аналогично, если x>0, то при n, и поэтому для x>0 ряд сходится равномерно. Тогда его сумма является непрерывной, а значит, измеримой функцией.

Задача 5. Доказать, что функция z = f(x, y), (x, y)  R² является измеримой на R², если f(x,y)=.

Решение. Поскольку функции z=[xy] и z=[x²+y²] простые, то они измеримы на плоскости. Измеримой для каждого номера n является функция . Из сходимости функционального ряда (что устанавливается с помощью признака сравнения) следует измеримость на R² функции f(x,y).

Задача 6. Для функции f построить последовательность простых измеримых функций, равномерно сходящуюся к f, если

Решение. Исходя из теоремы, для измеримой конечной на множестве A функции f(x) последовательность простых измеримых функций строится так: для каждого целого k на множестве . Поэтому для x  0 полагаем f_n(x)=0, а на множествах {x > 0 : } = {x>0 : }, k = 0,1,…,n –1 полагаем .

Задача 7. Доказать, что при n последовательность f_n(x)=sinⁿx+cosⁿx сходится к нулю почти всюду на R относительно меры Лебега.

Решение. При тех xR, для которых |sin x|<1 и |cos x|<1, имеем , . Если же xR таково, что sin x = 1 (или cos x = 1), то предел функции sinⁿx (соответственно cosⁿx) равен единице или не существует. Таким образом, рассмотрим множество A₀={xR: sin x=1 или cos x = 1} = {k : kZ}{1/2+k : kZ}. Множество A₀ – счётное (как объединение двух счётных множество) и поэтому (A₀)=0. Тогда для каждой точки xR\A₀ , и, следовательно, почти всюду последовательность f_n(x) сходится к f(x)=0.

Задача 8. Для последовательности f_n(x)=xⁿ, x[0,1] указать множество, на котором f_n(x) сходится равномерно, причём мера множества, на котором нет сходимости, может быть сделана сколь угодно малой.

Решение. Рассмотрим произвольное  > 0. Если  1, то в качестве X_ возьмём, например, отрезок [0, 1/2]. Тогда (A_) = =1/2>(X)– = 1–, где X=[0,1]. , т.е. на [0,1/2] последовательность равномерно сходится к функции f(x)=0. Если же <1, то положим X_ = [0,1-/2], тогда (X_)=1-/2>(X)-=1-, т.е. (X\X_)< и = = 0.

Задача 9. Исследовать на сходимость по мере к функции f на измеримом множестве A следующие последовательности:

1. f_n(x)=xⁿ, x[0,1],

2. f_n(x)=cosⁿx, xR.

Решение. 1) Рассмотрим для   > 0 измеримое множество {x[0,1] : xⁿ  } = [,1]. Отметим, что когда  > 1, то множество пусто. Тогда = = 0 и поэтому на [0,1]. С другой стороны, xⁿ  0 почти всюду (см. пример), тогда по мере.

2) Пусть   1, тогда . Значит  {x  R : } = = +. Поэтому заданная последовательность не сходится по мере.

Задание 1. Пусть X = [-1,1[, на X задана мера Лебега. Выяснить, является ли функция f: 1)измеримой; 2)ограниченной; 3)простой. Найти все её точки непрерывности и точки разрыва. Построить эквивалентную функцию с минимальным множеством точек разрыва.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

Задание 2. Доказать, что функция y = f(x), xRⁿ измерима на Rⁿ.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

Задание 3. Для заданной на отрезке [0,1] функции f построить последовательность f_n простых функций, равномерно сходящуюся к f.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

Задание 4. Исследовать на сходимость следующие последовательности:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14.