
- •Тема 5. Интеграл Лебега-Стилтьеса, функции с ограниченным изменение
- •1. Заряды. Функции с ограниченным изменением.
- •Основные свойства функций ограниченной вариации
- •2. Интеграл Лебега-Стилтьеса. Связь с интегралом Римана-Стилтьеса
- •Основные свойства интеграла Римана-Стилтьеса.
- •Примеры решения задач
- •Для функции
2. Интеграл Лебега-Стилтьеса. Связь с интегралом Римана-Стилтьеса
Пусть задано
измеримое пространство
![]() и заряд
и заряд
![]() .
Поскольку заряд можно представить в
виде разности двух конечных мер
.
Поскольку заряд можно представить в
виде разности двух конечных мер
![]() и
и
![]() ,
то функция интегрируемая по каждой из
мер будет интегрируема по заряду. Этот
интеграл обладает всеми свойствами
обычного интеграла Лебега.
,
то функция интегрируемая по каждой из
мер будет интегрируема по заряду. Этот
интеграл обладает всеми свойствами
обычного интеграла Лебега.
Рассмотрим пример интеграла по заряду.
Пусть на отрезке
![]() задана неубывающая непрерывная слева
функция g.
Тогда эта функция на -алгебре
множеств
задана неубывающая непрерывная слева
функция g.
Тогда эта функция на -алгебре
множеств
![]() определяет конечную меру Лебега-Стилтьеса.
Интеграл Лебега, построенный по этой
мере, называют интегралом
Лебега-Стилтьеса
и обозначают
определяет конечную меру Лебега-Стилтьеса.
Интеграл Лебега, построенный по этой
мере, называют интегралом
Лебега-Стилтьеса
и обозначают
![]()
Рассмотрим частные случаи:
-
Функция g – функция скачков (т.е.
 – дискретная мера), тогда
– дискретная мера), тогда
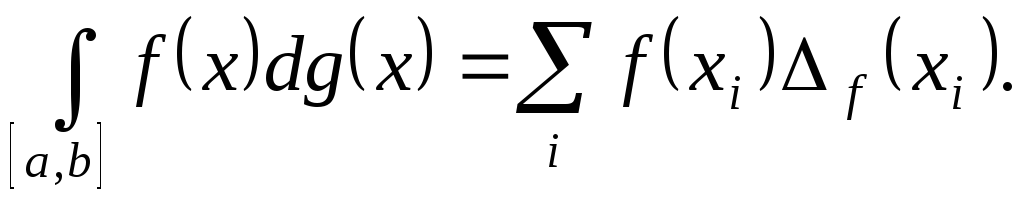
-
Функция g – абсолютно непрерывна, тогда
![]()
т.е. обычный интеграл Лебега.
-
Функция g, непрерывная слева на [a,b], функция с ограниченным изменением. Тогда ее можно представить в виде разности двух неубывающих функций
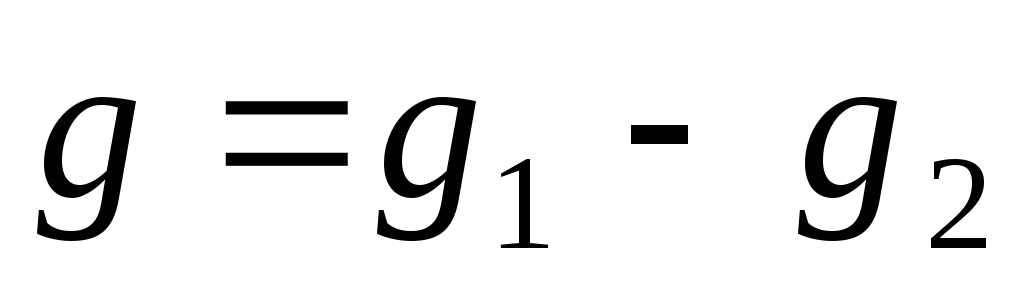 непрерывных слева. Поэтому
непрерывных слева. Поэтому
![]()
Ясно,
что это интеграл Лебега по заряду
![]() ,
построенному по функции с ограниченным
изменением. В общем случае он не сводится
к интегралу Лебега.
,
построенному по функции с ограниченным
изменением. В общем случае он не сводится
к интегралу Лебега.
Помимо интеграла Лебега-Стилтьеса на прямой можно определить интеграл Римана-Стилтьеса. Он вводится как предел интегральных сумм, аналогичных обычным интегральным суммам Римана. Пусть f – произвольная функция на [a,b], g – непрерывная слева функция с ограниченным изменением.
Рассмотрим некоторое
разбиение отрезка [a,b]:![]() ,
,
![]()
![]() выберем
выберем
![]() и составим интегральную сумму
и составим интегральную сумму
![]()
Если
эти интегральные суммы при
![]() имеют конечный предел, не зависящий от
способа разбиения отрезка и от выбора
точек
имеют конечный предел, не зависящий от
способа разбиения отрезка и от выбора
точек
![]() ,
то этот предел называют интегралом
Римана-Стилтьеса
от функции f
по функции g.
,
то этот предел называют интегралом
Римана-Стилтьеса
от функции f
по функции g.
Теорема 3. Если функция f непрерывна на [a,b], то ее интеграл Римана-Стилтьеса существует и совпадает с соответствующим интегралом Лебега-Стилтьеса.
Основные свойства интеграла Римана-Стилтьеса.
-
Теорема о среднем
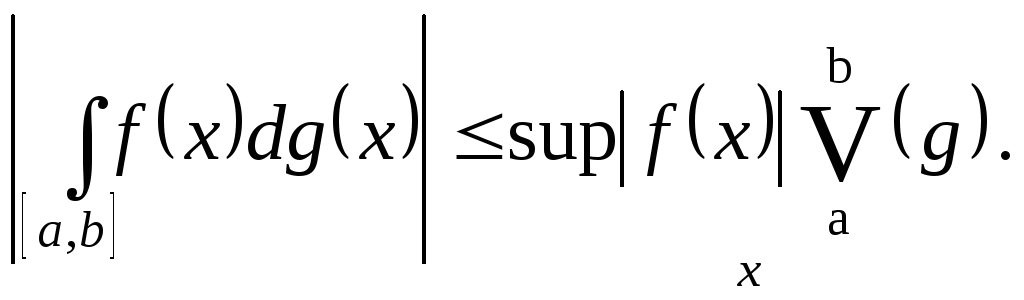
-
Если
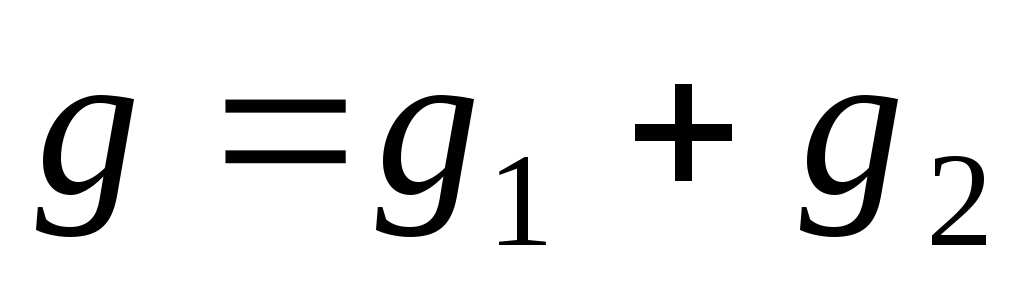 ,
то
,
то
![]()
-
Если
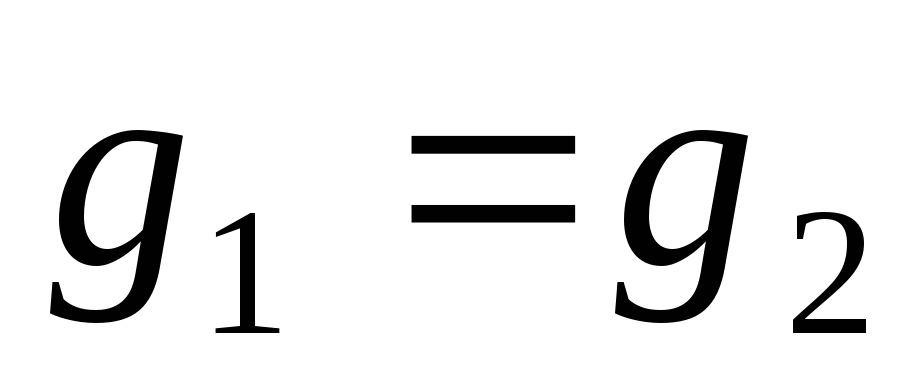 почти всюду, то
почти всюду, то
![]()
Теорема 4.
Пусть функция
![]() непрерывна [a,b],
а функция
непрерывна [a,b],
а функция
![]() имеет на [a,b]
всюду, кроме конечного числа точек
имеет на [a,b]
всюду, кроме конечного числа точек
![]() интегрируемую производную
интегрируемую производную
![]() .
тогда существует интеграл Римана-Стилтьеса
и выражается формулой:
.
тогда существует интеграл Римана-Стилтьеса
и выражается формулой:
![]()
![]()
Примеры решения задач
Задача
1. Пусть
функция F(x)
порождает меру Лебега-Стилтьеса на [
–2, 2 [. Доказать, что произвольная функция
f
(x)
интегрируема на [–2, 2 [ относительно
меры
![]() и
и
![]()
![]() если
F(x)=
если
F(x)=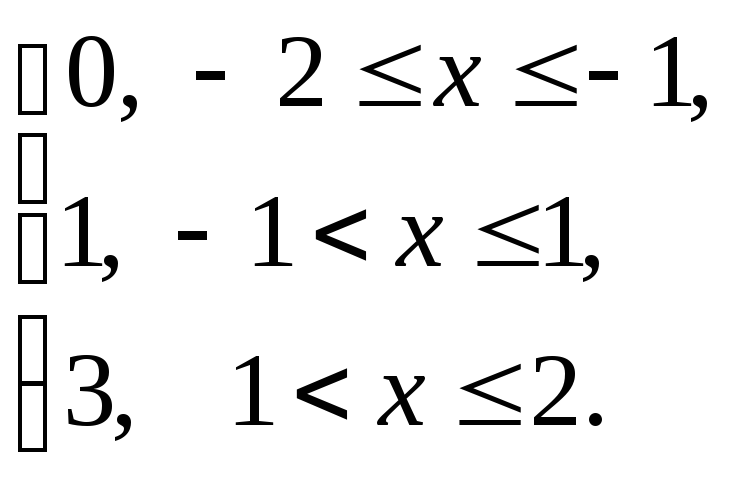
Решение.
Отметим, что все подмножества интервала
[-2,2[ измеримы и поэтому каждая функция
f(x),
x
[-2,2[ измерима относительно меры
![]() .
Представим полуинтервал [-2,2[ в виде
объединения непересекающихся множеств
[ –2, 2[ = [–2, –1[
{–1}
]–1,1[
{1}
]1,2[.
.
Представим полуинтервал [-2,2[ в виде
объединения непересекающихся множеств
[ –2, 2[ = [–2, –1[
{–1}
]–1,1[
{1}
]1,2[.
Множества
[-2,1[, ]-1,1[, ]1,2[ имеют меру нуль, так как
функция, порождающая меру
![]() ,
на этих множествах постоянна, а тогда
каждая функция f
(x)
интегрируема и интеграл от неё равен
нулю.
,
на этих множествах постоянна, а тогда
каждая функция f
(x)
интегрируема и интеграл от неё равен
нулю.
На множествах {-1} и {1} функция постоянна, а значит, простая. Поэтому
![]()
![]()
Следовательно, произвольная функция f (x) интегрируема на [-2,2[ и интеграл равен 2f (1)+f (–1). Данная функция будет интегрируема на всей числовой прямой, если
F(x)=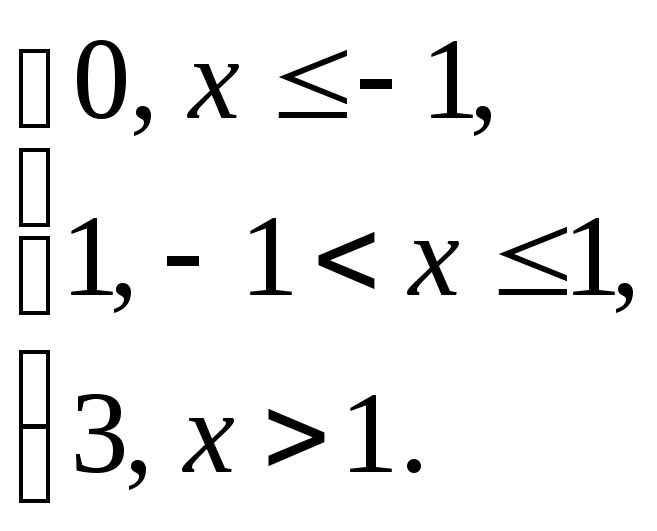 тогда
тогда
![]()
Задача 2. Вычислить интеграл Римана-Стилтьеса
![]() где
F(x)=
где
F(x)=
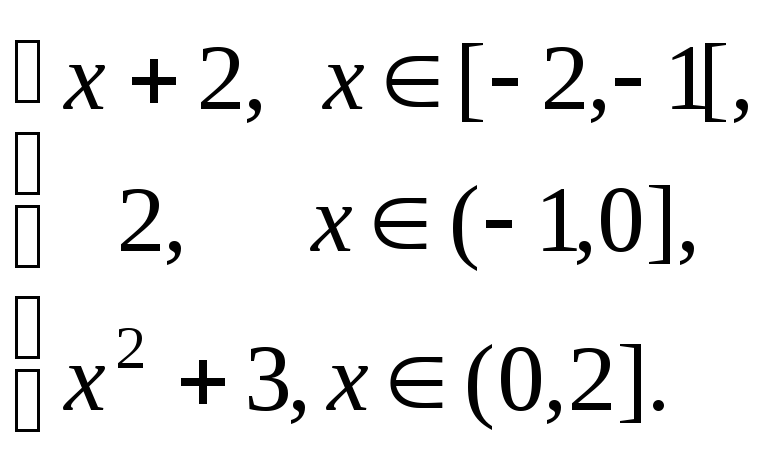
Решение.
Если функция f
(x)
непрерывна на [a,
b],
а функция F
(x)
имеет на [a,
b]
всюду, кроме конечного числа точек
![]()
![]() интегрируемую
по Риману производную
интегрируемую
по Риману производную
![]() ,
то существует интеграл Римана-Стилтьеса
и
,
то существует интеграл Римана-Стилтьеса
и
![]()
![]()
Тогда
![]()
Задача
3. Пусть
X=[0,1[,
S={[a,b[X},
h(x)
– некоторая неотрицательная интегрируемая
по Риману на отрезке [0,1] функция;
![]() Вычислить
Вычислить
![]()
Решение.
Построим последовательность простых
интегрируемых функций, равномерно
сходящуюся к
![]() Представим
Представим
![]() так, что
так, что
![]() По теореме о среднем для интеграла
Римана
По теореме о среднем для интеграла
Римана
![]() такая, что
такая, что
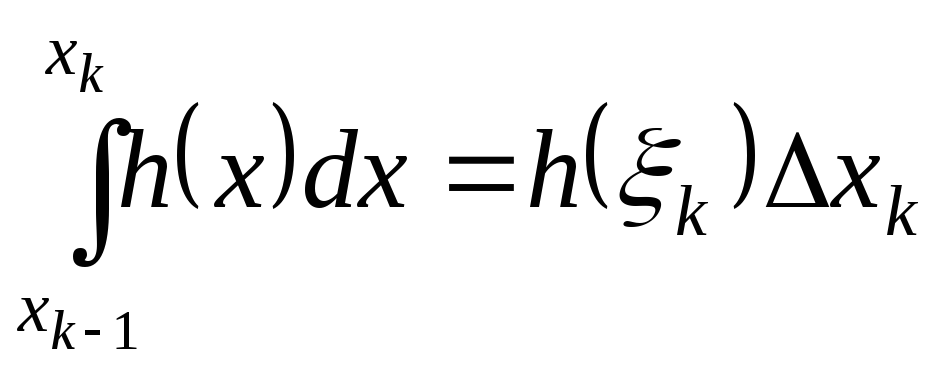 ,
т.е.
,
т.е.
![]() .
.
Положим
![]() для
для
![]() ,
тогда
,
тогда
![]()
![]() и
и
![]() равномерно сходится к
равномерно сходится к
![]() т.к. при
т.к. при
![]()
![]()
![]()
![]()
![]() есть
интегральная сумма Римана, построенная
для непрерывной функции
есть
интегральная сумма Римана, построенная
для непрерывной функции
![]() на отрезке [0,1]. Так как при
на отрезке [0,1]. Так как при
![]() ,
,
![]() ,
то
,
то
![]() Итак,
Итак,
![]()
Задача 4. Пусть на [0,3[ задана мера Лебега–Стилтьеса, порожденная функцией
F(x)
=
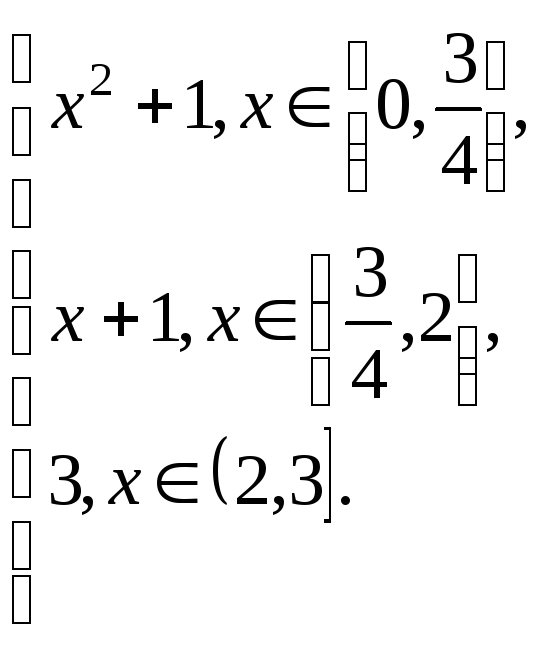
Проверить, что F не убывает и непрерывна слева. Найти:
1) меру одноточечного множества;
2) промежутки, на которых эта мера совпадает с мерой Лебега;
3) промежутки,имеющие нулевую меру;
4) промежутки, на которых эта мера абсолютно непрерывна относительно меры Лебега;
5) найти меру канторова множества K и меру множества рациональных чисел на [0,3[.
