Chuprigin_O_A_-_Matematicheskiy_analiz_predel_nepreryvnost_differentsiruemost_pdf

Определение 1 (по Коши). Число А называется пределом функции f(x) в точке а, åñëè

0 ( ) 0 : õ : 0 | õ à | | f(x) A | .

Определение 2 (по Гейне). Число А называется пределом функции f(õ) в точке а, если для любой сходящейся к à последовательности значений аргумента (õï) такой, ÷òî õï à ï, соответствующая последовательность значений функции (f(xn)) сходится к А или в краткой записи:

(xn) : xn a, xn a n f(xn) A. Обозначения предела функции в точке

lim f(x) A èëè f(x) A ïðè x a.

x a

Выражение «предел функции в точке à» часто заменяют выражением «предел функции при õ, стремящемся к à» или, коро- че, «предел функции при õ à».

Первое определение (по Коши) называют определением предела функции на языке « - », второе — определением на языке последовательностей.

Подчеркнем, что предел функции в точке à зависит лишь от поведения функции в проколотой окрестности точки à (âåäü 0 | õ à |, ò. å. õ à, аналогично õï à) и не зависит от того, определена ли функция в самой точке à или не определена.

2.10.3. Доказательство равносильности двух определений предела функции

1. Пусть À является пределом функции f(x) в смысле первого определения, т. е.

0 ( ) 0 : õ : 0 | õ à | | f(x) A | .

Надо показать, что À будет пределом и в смысле второго определения. Это означает, что

(õï) : õï à, õï à должно выполняться условие lim f(xn) A.

n

Òàê êàê lim xn à, òî N : n N | xn à | , где взято из первого определения. А тогда (по первому определению) | f(xn) A | .

Следовательно, lim f(xn) A.

n

112

2. Пусть À есть предел функции в смысле второго определения, т. е. (õï) : õï à, õï à f(xn) A.

Предположим от противного, что число À не является пределом по первому определению, это значит:

0 0 : 0 õ : 0 | õ à | , íî | f(x ) A | 0.

Âкачестве будем брать все числа вида ï 1 / ï (ï 1, 2, 3, ...),

èдля каждого из них найдется точка xï такая, что

0 | õï à | ï, íî | f(xn) A | 0.

Из этих соотношений видно, что õï à (õï à). А тогда, со-

гласно первому определению, lim f(xn) A. Но этого не может

n

áûòü, òàê êàê n имеем неравенство | f(xn) A | 0. Полученное противоречие и завершает доказательство.

2.10.4. Отрицание определений предела функции

Сформулируем отрицания определений предела функции в точке.

Отрицание определения 1 (по Коши). A lim f(x), åñëè

x a

0 : 0 õ : 0 | õ à | è | f(x) A | .

Отрицание определения 2 (по Гейне). A lim f(x), åñëè

x a

(õï) : õï à, õï à ï, íî lim f(xn) A.

n

Исходя из определения предела по Коши, утверждение, что функция f(x) не имеет предела в точке à, запишется следующим образом:

lim f(x) не существует, åñëè À 0 : 0 õ : 0 | õ à |

x a

è | f(x) A | .

При решении конкретных примеров удобнее пользоваться отрицанием определения на языке последовательностей. Для того

чтобы доказать, что lim f(x) не существует, достаточно либо ука-

x a

зать такую последовательность (õï), сходящуюся к à è õï à ï, чтобы последовательность f(xn) расходилась, либо указать две

сходящиеся к à последовательности (xn) è (xn) такие, чтобы соот-

ветствующие последовательности значений функции f(x ) è f(x )

n n

имели разные пределы.

113

Пример 1. Найти lim f(x), ãäå f(x) x2 x 2.

(условие xn 1 n позволило нам сократить дробь на xn 1).

Следовательно, lim f(x) 3.

x 1

II с п о с о б. Будем пользоваться определением предела на языке « - ». Для любого 0 найдем ( ) 0 такое, чтобы из нера-

Следовательно, достаточно взять . Итак,

0 0 : õ : 0 | õ 1 | | f(x) 3 | .

Пример 2. Доказать, пользуясь определением предела функ-

öèè, ÷òî lim x2 4.

x 2

I с п о с о б. Для любой последовательности (õï) такой, что õï 2, õï 2 имеем

lim x2n 4,

n

что и требовалось доказать.

II с п о с об. Для любого 0 найдем такое ( ) 0, чтобы для всех õ, удовлетворяющих неравенству 0 | õ 2 | выполнялось неравенство | õ2 4 | èëè | õ 2 | | õ 2 | .

Еcли предположить выполнение неравенства | õ 2 | , òî | õ 2 | | (õ 2) 4 | 4, а тогда | õ 2 | | õ 2 | ( 4).

114

Следовательно, для выполнения неравенства | õ2 4 | достаточно взять таким, чтобы ( 4) или 2 4 0. Так как должно быть положительíûì, то из двух решений последнего равенства берем 2 4 . Èòàê,

0 4 2 0 : õ : 0 | õ 2 | | õ2 4 | .

III с п о с о б. В предыдущем рассмотрении мы нашли для данного наибольшее , при котором гарантировано неравенство | õ2 4 | . Однако в определении предела по Коши достаточно указать хотя бы одно (не обязательно наибольшее), чтобы неравенство 0 | õ 2 | влекло неравенство | õ2 4 | . Поэтому задачу об отыскании можно облегчить, если заранее принять, например, 1, т. е. рассматривать õ лишь на интервале (1, 3). Учитывая, что 1 õ 3, получаем неравенство

| õ2 4 | | õ 2 | | õ 2 | 5 | õ 2 |,

из которого видно, что достаточно взять / 5, чтобы из неравенства | õ 2 | следовало неравенство | õ2 4 | . Но поскольку мы приняли ранее 1, то нужно взять min (1, / 5). Итак, мы получаем требуемое:

0 min(1, / 5) : õ : 0 | õ 2 | | õ2 4 | .

Практический совет. Чтобы доказать равенство lim f(x) A,

x a

пользуясь определением предела по Коши, обычно поступают следующим образом: выбирают некоторую окрестность точки à, например (a c, a c), è äëÿ âñåõ õ из этой окрестности стараются получить оценку вида | f(x) A | M | x a |. Тогда, очевидно, в качестве можно взять min(ñ, / Ì).

Пример 3. Доказать, что функция f(x) sin 1 , определенная x

äëÿ âñåõ õ 0, не имеет предела в точке õ 0.

Покажем, что в точке x 0 функция f(x) не удовлетворяет определению предела по Гейне. Для этого возьмем две последова-

115

для них соответствующие последовательности значений функции

соответствующая последовательность значений функции f(xn)

2.11. ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИЙ

2.11.1. Аналоги теоремам о пределах последовательностей

Предел функции f(x), исходя из определения по Гейне, сводится к пределу последовательности f(xn). Этот факт позволяет нам все доказанные (см. п. 2.2) теоремы о сходящихся последовательностях без труда распространить на пределы функций.

Сформулируем несколько утверждений, являющихся аналогами теоремам 3, 4 и 5 п. 2.2.

Теорема 1. Пусть f(x) è g(x) определены в проколотой окрестно-

сти точки à è lim f(x) A, lim g(x) B. Тогда существуют пре-

x a x a

делы суммы, разности, произведения и частного этих функций, причем

lim[f(x) g(x)] A B; lim[f(x) g(x)] A B;

Теорема 2. Пусть f(x) è g(x) определены в проколотой окрестности точки à è f(x) g(x) в указанной окрестности. Тогда если существуют пределы этих функций при x a, òî

lim f(x) lim g(x).

x a x a

116

Теорема 3. Пусть f(x), h(x) è g(x) определены в проколотой окрестности точки à è f(x) h(x) g(x) в указанной окрестно-

сти. Пусть, кроме того, существуют и равны пределы lim f(x)

x a

lim g(x) A. Тогда существует lim h(x) и он равен А.

x a x a

2.11.2. Предел сложной функции

Пусть X есть область определения функции y (x), à Y — множество ее значений. Пусть, далее, f(y) определена на множестве Y.

Теорема 4. Если существуют пределы lim (x) b, lim f(y) c

x a y b

è (x) b ïðè x a, то существует также предел сложной функции f( (x)) ïðè õ à, равный с, ò. å.

lim f( (x)) lim f(y).

x a y b

При доказательстве будем пользоваться определением предела функции по Гейне. Пусть (õï) — произвольная последовательность, сходящаяся к à, õï à ï. Тогда последовательность óï (õï) сходится к числу b è óï b ï. Но в таком

случае в силу существования предела lim f(y) c последова-

y b

тельность f(yn) f( (xn)) сходится к числу ñ, что и требовалось доказать. Замечание 1. Практическая ценность теоремы заключается в том, что она позволяет вычислять пределы функций, переходя от переменной õ к новой переменной ó õ), что мы будем весь-

ма часто использовать.

Замечание 2. Условие теоремы (õ) b ïðè õ à опустить нельзя. В самом деле, пусть (x) x sin 1, à f(y) 1, åñëè ó 0,

lim f( (x)) не существует. Причина такой ситуации в том, что

x 0

функция (õ) имеет нули в любой окрестности точки õ 0.

117

2.12. ОДНОСТОРОННИЕ И НЕСОБСТВЕННЫЕ ПРЕДЕЛЫ

2.12.1. Односторонние пределы

Кроме рассмотренного нами (см. п. 2.10.2) предела функции в точке, существуют также понятия предела функции в точке слева (или левостороннего предела) и предела функции в точке справа (или правостороннего предела).

Если в определении предела функции потребовать, чтобы õ стремилось к à, оставаясь все время левее (правее) точки à, то получим определение предела слева (справа) в точке à. При рассмотрении предела слева (справа) в точке à естественно требовать, чтобы функция была определена на некотором полуинтервале [b, a) (полуинтервале (a, b]).

Определение 1 (по Коши). Число А называется пределом функции f(x) в точке à справа (слева), åñëè

0 ( ) 0 : õ : à õ à (à õ à) | f(x) A | .

Определение 2 (по Гейне). Число А называется пределом функции f(x) в точке à справа (слева), åñëè

Правосторонний и левосторонний пределы в точке à принято обозначать так:

lim f(x) èëè f(a 0), lim f(x) èëè f(a 0) соответственно.

Åñëè à 0, то для предела справа используют также обозначе- ние lim f(x) èëè f( 0), для предела слева — lim f(x) èëè f( 0).

Из определений предела функции и односторонних пределов вытекают следующие утверждения.

1. Если существуют f(a 0) è f(a 0), причем f(a 0)

f(a 0) A, то существует и lim f(x) A.

x a

2. Если существует lim f(x) A, то существуют оба одно-

x a

сторонних предела f(a 0) è f(a 0), причем f(a 0) f(a 0) A. Однако функция может иметь односторонние пределы и при отсутствии предела в точке à. Естественно, что это возможно лишь в случае, когда f(a 0) f(a 0). Указанное обстоятельст-

118

во используют для доказательства отсутствия предела функции в точке à.

В точке õ 0 функция не определена. Очевидно, что f(x) 1

äëÿ õ 0 è f(x) 1 äëÿ õ 0. Тогда (õï) : õï 0 è õï 0 имеем

Аналогично lim f(x) 1.

Замечание 1. Очевидно, что все теоремы о пределах функций (см. п. 2.11) переносятся на односторонние пределы. Например, если

2.12.2. Несобственные пределы

Предел функции lim f(x) A будем называть несобственным

x a

пределом, если в его записи à èëè À заменены символами + , или .

2.12.2.1. Конечный предел функции при x

Для функций, областью определения которых является полупрямая (ñ, + ) или полупрямая ( , d), вводятся понятия предела при х + и соответственно ïðè x . Эти пределы обозна-

÷àþò òàê: lim f(x) è lim f(x).

x x

Определение 3 (по Коши). lim f(x) A, åñëè

0 $ $( ) 0 : õ $ | f(x) A | .

Определение 4 (по Гейне). lim f(x) A, если для любой беско-

нечно большой последовательности (õï), ãäå õï ñ ï, предел

lim f(xn) A.

n

119

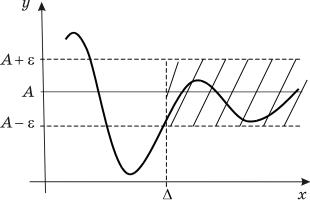
Геометрический смысл. lim f(x) A означает, что 0

$ 0 такое, что x $ график функции y f(x) будет нахо-

диться между прямыми y À è y À (ðèñ. 2.3).

Аналогично определяется lim f(x) A.

x

Åñëè lim f(x) lim f(x) A, то пишут lim f(x) A.

x x x

Ðèñ. 2.3

2.12.2.2. Бесконечный предел функции при x a

Рассмотрим случай, когда в записи lim f(x) A вместо À

x a

стоят символы + , или .

Определение 5. Будем говорить, что функция f(x) стремится к бесконечности при x, стремящемся к à справа, åñëè

Å 0 (Å) 0 : õ : à õ à | f(x) | Å.

Бесконечный предел при õ, стремящемся к à справа, записывают следующим образом:

lim f(x) èëè f(a 0) .

x a 0

Если в определении 5 вместо неравенства | f(x) | Å выполняется неравенство f(x) E (f(x) E), то пишут

lim f(x) èëè f(a 0)

x a 0

( lim f(x) èëè f(a 0) ).

x a 0

Аналогично определяются бесконечные пределы при õ, стремящемся к à слева (в этом случае неравенство a x a , ôè-

120

гурирующее в определении 5, нужно заменить неравенством a x a).

Åñëè f(x) стремится к бесконечности ( , ) при x, стремящемся к à справа и слева, то пишут

lim f(x) ( , ).

x a

Приведенные выше определения легко перефразировать на

языке последовательностей. Например, запись lim f(x)

x a 0

означает, что (xn) : xn a è xn a (f(xn)) является бесконеч- но большой.

2.12.2.3. Бесконечный предел функции при x

Аналогичным образом определяются несобственные пределы,

когда в записи lim f(x) A вместо à è À одновременно стоят сим-

x a

âîëû , èëè . Например:

1.Запись lim f(x) означает, что

Å 0 (Å) 0 : õ : õ | f(x) | Å.

2.Запись lim f(x) означает, что

Å 0 (Å) 0 : õ : õ f(x) Å.

3.Запись lim f(x) , означает, что

x

Å 0 (Å) 0 : õ : | õ | | f(x) | Å.

Замечание 2. Во избежание недоразумений условимся в дальнейшем в следующей терминологии: если сказано, что некоторая функция в данной точке имеет предел, то всегда будем иметь в виду, что этот предел конечный. Cлучай бесконечного предела будем оговаривать особо.

Пример 2. Пользуясь определением предела, доказать, что

а) Надо показать, что E 0 (E) 0: x : x

| a1/x 1 | E. Òàê êàê à1/õ 1 õ 0, то нам нужно показать,

÷òî a1/x 1 E èëè a1/x 1 E. Логарифмируя последнее нера-

121