Инерциальные_свойствава_твердого_тела.pdf_(182_Кб) / metod_mehanika / Инструкции к лабораторным работам / Механика старые / 22. Связанные системы

Рис. 1

Работа 22. КОЛЕБАНИЯ СВЯЗАННЫХ СИСТЕМ

Задание: ознакомиться с основными понятиями, используемыми при описании колебаний связанных систем.

Оборудование и принадлежности: установка для проведения измерений, линейка, штангенциркуль, весы.

ОПИСАНИЕ УСТАНОВКИ

Общий вид прибора представлен на рис.1. Основание 1 оснащено регулируемыми ножками, обеспечивающими выравнивание прибора. В основании закреплена колонка 2. На колонке закреплена втулка 3 и кронштейн 4. На стержне 5 втулки находятся подвесы 6, на которых с помощью шариковых подшипников подвешены два маятника и стержень 7, возбуждающий колебания. Маятник состоит из стержня 8 и перемещаемого груза 9. Маятники сопряжены друг с другом при помощи двух пружин 10, закрепленных в специальной С-образной обойме 11, которую можно перемещать вдоль стержней маятников. Возбуждение колебаний осуществляется при помощи приводного диска, закрепленного на валу электродвигателя, который, двигая стержень 7, сопряженный при помощи двух пружин 10 со стержнем маятника, возбуждает его колебания. К кронштейну 4 прикреплена угловая шкала, при помощи которой определяется амплитуда колебаний. К нему же прикреплен фотоэлектрический датчик, световой поток которого пересекает стержень одного из маятников.

ЭЛЕМЕНТЫ ТЕОРИИ

Рис. 2

Рассмотрим систему, состоящую из небольшого шарика массы m, подвешенного на легкой нити длиной l (модель математического маятника). Если шарик сместить из положения равновесия и отпустить (рис. 2), то он будет совершать колебания. По второму закону Ньютона ускорение шарика определяется уравнением:

(1)

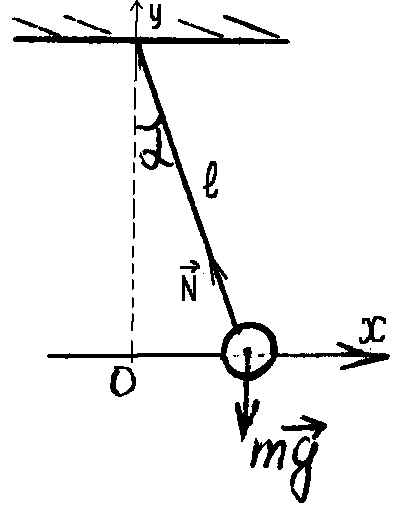
Вектор направлен к положению равновесия, по касательной к траектории шарика (перпендикулярно нити). Его проекции на оси координат (рис. 2) имеют вид:

ma_x = -Nsin, (2)

ma_y = Ncos - mg. (3)

Из этих уравнений находим:

N = m(a_y + g)/cos,

a_x = -(a_y + g)tg.

При малых отклонениях нити от положения равновесия tg  sin = x/l, a_y = -asin  0 (a_y « g). Тогда: a_x = -(g/l)x, или

(2)

Уравнение (2) - это уравнение гармонических колебаний переменной х. Его решением является функция вида x = Asin(t + ), где - циклическая частота гармонических колебаний. Важно помнить, что движение шарика будет описываться уравнением (2) только при условии, что угол отклонения нити небольшой.

Рис. 3

Если при колебаниях шарика на него действует некоторая сила (рис. 3), то уравнение (1) примет вид:

(1a)

При малых углах отклонения нити это уравнение в проекции на ось ОХ можно записать в виде:

(2a)

Число независимых переменных, которые задают положение тела в пространстве, называют числом степеней свободы тела. Материальная точка имеет 3 степени свободы. Абсолютно твердое тело имеет 6 степеней свободы (кроме 3 декартовых координат, определяющих положение центра масс тела, необходимо указать 3 угла, определяющие повороты тела относительно выбранных осей координат). Если движение тела ограничено (на него наложены связи), то число степеней свободы тела уменьшается.

Шарик, подвешенный на нити, может совершать колебания вдоль 2-х взаимно перпендикулярных направлениях - он имеет 2 степени свободы. Если колебания шарика происходят только в одной плоскости, то для описания его колебаний достаточно указать одну координату - угол отклонения нити  или смещение шарика х. В этом случае возбуждается только одна степень свободы шарика.

Рис. 4

Если система обладает несколькими степенями свободы, то при отклонениях от положения равновесия возможны одновременно колебания по всем степеням свободы. В том случае, когда колебания, соответствующие каждой из степеней свободы, независимы друг от друга, т.е. не могут обмениваться друг с другом энергией, рассмотрение движения системы с несколькими степенями свободы сводится к изучению движения по каждой степени свободы с последующим суммированием движений.

Наличие связи, обеспечивающей возможность обмена энергией между различными степенями свободы, приводит к возникновению колебаний с частотами, отражающими специфику связи. В этом случае говорят о связанных системах. Примером такой системы могут служить два маятника, соединенные пружиной (рис. 4). Такая система имеет 4 степени свободы. Колебательные движения, относящиеся к каждой из четырех степеней свободы, являются зависимыми друг от друга. Если один из маятников вывести из положения равновесия, отклонив его одновременно и в плоскости маятников, и в перпендикулярном этой плоскости направлении, то колебания первого маятника возбуждают колебания второго, связанные с его степенями свободы.

Несмотря на сложность движения двух связанных маятников, оно всегда может быть представлено как суперпозиция четырех гармонических колебаний, частоты которых называются нормальными частотами связанной системы. Число нормальных частот равно числу степеней свободы. Существуют общие методы нахождения нормальных частот (см. [2]). Рассмотрим их применение для описания системы связанных маятников, ограничиваясь случаем, когда возбуждаются только две степени свободы (рис. 5, колебания происходят в одной плоскости). Будем считать, что система подвержена малым возмущениям. Это означает, что силы, действующие на маятники, пропорциональны их отклонениям от положения равновесия.

Рис. 5

При колебаниях маятников из-за деформации пружины возникают силы, пропорциональные её удлинению. Удлинение пружины равно x₂-x₁, где х₁ и х₂ - смещение первого и второго шарика из положения равновесия. Следовательно, на маятники действуют силы упругости

F_1x = -F_2x = (x₂ - x₁), (3)

где  - коэффициент упругости пружины. Поэтому уравнения движения шариков с учетом сил связи посредством пружины имеют вид:

(4a)

(4b)

где m - масса каждого из одинаковых шариков. В каждое из уравнений (4a) и (4b) входят две переменные величины: х₁ и х₂. Складывая левые и правые части этих уравнений, а затем, вычитая, получим уравнения, содержащие только одну переменную величину: z₁ = (x₁ + x₂) и z₂ = (x₁ - x₂)

(5a)

(5b)

Уравнения (5a) и (5b) аналогичны уравнению (2) - это уравнения гармонических колебаний переменных z₁ и z_2. Циклические частоты этих колебаний (нормальные частоты) равны:

, , (6)

Для используемой в работе установки нормальные частоты равны:

, , (6)

где b - расстояние между точкой закрепления пружины и точкой подвеса маятника. Решения уравнений (5a) и (5b) имеют вид:

, . (7)

Рис. 6

Отсюда для отклонений x₁ и x₂ путем сложения и вычитания левых и правых частей получаем:

, (8a)

, (8b)

В качестве примеров возможных колебаний данной системы рассмотрим следующие:

Рис. 7

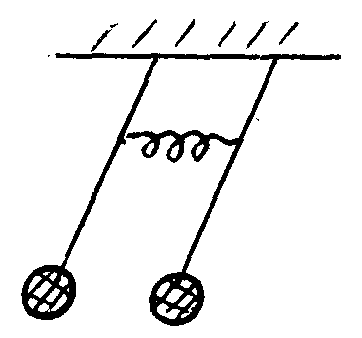
а) x₁ - x₂ = 0. Тогда . Маятники колеблются как единое целое с частотой . Колебания называются синфазными (рис.6);

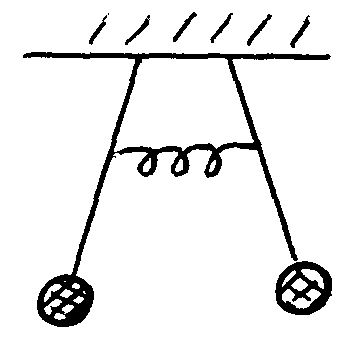
б) x₁ + x₂ = 0. В этом случае и колебания называются противофазными (рис.7). Частоты ₁ и ₂ - соответственно частоты синфазных и противофазных колебаний.

Пусть k мало. Отведем 1-й маятник на угол , второй при этом задержим в положении равновесия. Тогда из (8a,b) получаем, что в момент времени t = 0:

(9)

(10)

(11)

(12)

Из (9) - (12) при ₁  ₂ , т.е. ₁ - ₂ « , получаем:

A₀ = B₀ = l. (13)

С учетом этого уравнения (8) принимают вид:

, (14)

. (15)

Рис. 8

Очевидно, что полученные колебания имеют характер биений с периодом

(16)

При действии на систему силы синусоидального характера наблюдается так называемый двугорбый резонанс (рис.8). Колебания обоих маятников с максимальной амплитудой будут наблюдаться тогда, когда одна из частот колебаний равна частоте внешней силы.

Порядок выполнения задания

1. По формулам (6) для ₁ и ₂ рассчитать частоты синфазных и противофазных колебаний при k = 6,5 Н/м, m = 0,150 кг, l = 0,300 м, b = 0,250 м. Установить соответствующие грузы на стержнях маятников и соединить их пружиной. По формуле  = 2n/t, где n - число колебаний, t - время n колебаний (n = 5), определяют ₁ и ₂. Для этого отклонить маятники сначала в одну сторону на 5-6 градусов, затем в противоположные стороны на 5-6 градусов и определить по миллисекундомеру время n колебаний. Сравнить полученные результаты.

2. Отклонить второй маятник на угол , удерживая первый в положении равновесия. Отпустить маятники. Определить время, через которое первый маятник опять будет неподвижен. По формуле (16) рассчитать период биений. Сравнить полученное значение с измеренным на опыте.

3. Исследовать зависимость периода биений T от связи маятников, характеризуемой расстоянием b пружины от точки подвеса маятников (b изменять от 5,0 см до 25,0 см через 5,0 см).

4. Убедиться в возникновении резонанса при действии на систему периодической силы. Для этого соединить пружинами стержень 7 со стержнем маятника, включить двигатель и, изменяя частоту вынуждающей силы, добиться максимального отклонения маятников от положения равновесия. Определить частоту, при которой возникает резонанс. Сравнить полученное значение с измеренными в п.1.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какая система называется связанной? Какие колебания называются нормальными?

2. Будут ли маятники обмениваться энергией при синфазных колебаниях? При противофазных?

3. Охарактеризуйте движение связанной системы в случае слабой связи.

ЛИТЕРАТУРА

1. Кембровский Г.С. Приближённые вычисления и методы обработки результатов измерений в физике. -Минск: Изд-во "Университетское", 1990. -189 с.

2. Матвеев А.Н. Механика и теория относительности. -М.: Высшая школа, 1986. -320 с.

3. Сивухин Д.В. Общий курс физики. М.: Наука, 1989 Т. 1. Механика. -576 с.

4. Физический практикум. Под ред. Кембровского Г.С. -Минск: Изд-во "Университетское", 1986. -352 с.

11