Инерциальные_свойствава_твердого_тела.pdf_(182_Кб) / metod_mehanika / Инструкции к лабораторным работам / Механика старые / 7. Слож. гармонич. колебаний

Работа 7. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

Задание: получить на экране осциллографа фигуры Лиссажу и картину биений. Определить частоту _х генератора Г_х.

Оборудование и принадлежности: осциллограф, два звуковых генератора, соединительные провода.

ЭЛЕМЕНТЫ ТЕОРИИ

Колебания системы с двумя степенями свободы. Переход от колеблющихся систем с одной степенью свободы к системам с несколькими степенями свободы приводит к качественным изменениям свойств движения: в таких системах возможны колебания с разными частотами. Их совокупность - частотный спектр - тем богаче, чем большим числом степеней свободы обладает система.

В случае малых колебаний любая линейная комбинация гармонических колебаний есть один из возможных видов движения колеблющейся системы. В этом заключается физический смысл принципа суперпозиции (сложения) колебаний в системах с несколькими степенями свободы.

Сложение взаимно перпендикулярных колебаний. Пусть частица одновременно участвует в двух взаимно перпендикулярных колебаниях одинаковой частоты  совершающихся вдоль осей Х и Y, по законам

(1)

(2)

где А₁ и А₂ - амплитуды колебаний; ₀ - начальная фаза второго колебания, совпадающая в нашем случае с разностью фаз складываемых колебаний. Найдем траекторию частицы. Для этого из (1) и (2) исключим время t. Тогда получим

(3)

Это - уравнение эллипса. Размер и ориентация его осей зависят от значений А₁, А₂ и ₀ .

При ₀= 0 или ₀=  эллипс вырождается в прямую линию:

(4)

Рис. 1

В этом случае результирующее движение (рис. 1) является гармоническим колебанием, происходящим с частотой  и амплитудой

(5)

При ₀=  /2 из уравнения (3) получим

Рис. 2

(6)

т.е. частица движется по эллипсу с полуосями A₁ и A₂, ориентированными вдоль осей Х и Y соответственно (рис. 2). при ₀ =  /2 движение происходит по часовой стрелке, а при ₀ =  /2 - в обратном направлении. При равенстве амплитуд A₁ и A₂ эллипс вырождается в окружность.

Рис. 3

Если частота ₁  ₂ , то частица описывает кривые более сложного вида (рис.3). При простых кратных отношениях между частотами кривые замкнутые (их называют фигурами Лиссажу). Они вписаны в прямоугольник со сторонами, равными удвоенным амплитудам складываемых колебаний. Отношение частот

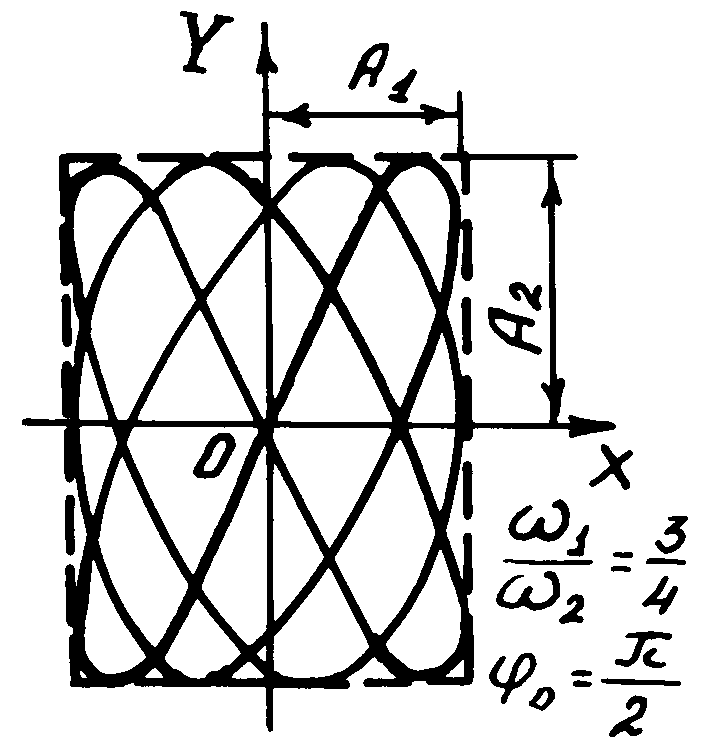
(7)

где n₁ и n₂ - число касаний фигуры Лиссажу с горизонтальной и вертикальной сторонами ограничивающего прямоугольника. Если отношение ₁/₂- число иррациональное, то траектория частицы незамкнутая и вместо фигуры Лиссажу получается область, сплошь заполненная траекторией движущейся частицы.

Биения. Рассмотрим сложение двух колебаний, происходящих вдоль одной прямой с частотами ₁ и ₂ , незначительно отличающимися друг от друга (  ₁- ₂<< ₁ и << ₂). Пусть в начальный момент времени фазы складываемых колебаний одинаковы. Тогда эти колебания запишутся в виде

и (8)

Найдем сумму двух таких колебаний, предположив для простоты сначала, что их амплитуды одинаковы (A₁ = A₂):

(9)

Рис. 4

Отсюда видно, что результирующее колебание происходит с частотой (₁+₂)/2, а амплитуда колебаний со временем изменяется в пределах от 2A₁ до 0 по закону (рис. 4). Значение 2A₁ достигается тогда, когда фазы складываемых колебаний совпадают, а нуль - когда фазы противоположны. Периодическое изменение результирующей амплитуды, получающееся при сложении колебаний, совершающихся с близкими частотами и вдоль одной прямой, называют биениями. Циклическая частота биений   ₁  ₂, период биений T_б = 2/ (см. рис.4) и частота биений _б = 1/T_б = ₁  ₂, где ₁ и ₂- частоты складываемых колебаний.

Рис. 5

Если амплитуды складываемых колебаний не равны (A₁  A₂), то максимальное значение амплитуды результирующего колебания равно A₁+A₂, а минимальное  А₁-А₂. В этом случае биения выражены менее четко (рис.5). Частоты  , _б и период T_б определяются разностью частот складываемых колебаний и не зависят от их амплитуд и начальных фаз.

Наблюдать биения и другие случаи сложения колебаний можно с помощью электронного осциллографа и звуковых генераторов.

Порядок выполнения задания

1. Включить электронный осциллограф и звуковые генераторы.

2. Изучить сложение взаимно перпендикулярных колебаний. Для этого подключить выход звукового генератора на Х-вход осциллографа, а контрольный сигнал осциллографа - на Y-вход. Установить одинаковые амплитуды и получить на экране осциллографа кривые (фигуры Лиссажу), возникающие в результате сложения двух взаимно перпендикулярных колебаний. Отношения частот складываемых колебаний выбирать равными 1:1, 1:2, 1:3, 2:3, 3:4. Зарисовать наблюдаемые фигуры. Проверить правило (7).

Рис. 6

3. Получить биения. Для этого соединить звуковой генератор (ГЗ), генератор неизвестной частоты (Г_x) и электронный осциллограф (ЭО) по схеме, изображенной на рисунке 6.

Условием для получения отчетливой осциллограммы биений является равенство амплитуд складываемых колебаний. Наблюдаемые на экране ЭО амплитуды уравнивают следующим образом. На обоих генераторах ручками “Пределы шкал дБ” устанавливают одинаковые пределы, например 3V. Ручки “Сопрот. нагрузки” переводят в положение “АТТ.600”. Тумблер “Внутр.нагрузка 600 “ ставят в положение “Вкл.”. Ручками “Рег.выхода” (плавная регулировка) на каждом из генераторов устанавливают выходное напряжение порядка 1,5 В, что соответствует отклонению стрелки на вольтметре примерно до середины шкалы. На обоих генераторах ручками “Установка частоты” устанавливают частоту 10 кГц. Отключают генератор Г_x. Ручкой “Усиление” по оси Y добиваются на экране осциллографа амплитуды, равной 2 см. Затем отключают генератор ГЗ и подключают Г_x. Ручкой “Рег.выхода” (плавная регулировка) устанавливают такую же амплитуду. Подключив оба генератора и включив генератор развертки Г_р осциллографа в положение “30 - 130”, получают устойчивую осциллограмму биений.

4. Определить частоту _х генератора Г_х. Для этого получить биения два раза: один раз при частоте генератора ГЗ ₁, меньшей частоты _х, второй раз при частоте ₂, большей частоты _х . В первом случае частота биений _б _х₁, во втором  ^_б  ₂ _х. Частоты ₁ и ₂ подбирают так, чтобы выполнялось условие _б  ^_б (периоды пульсации амплитуды на экране осциллографа в обоих случаях были одинаковыми). Тогда

_х  ₁₂2. (10)

5. Провести ряд повторных наблюдений и найти <_x> .

6. Определить частоту колебаний _x по фигурам Лиссажу. Для этого включить генератор ГЗ на Y-вход осциллографа, а генератор Г_x- на Х-вход и несколько раз определять частоту _x по разным фигурам Лиссажу. Найти <_x>.

7. Сравнить значения <_x>, полученные разными методами.

Контрольные вопросы

1. Каковы особенности сложения гармонических колебаний систем с несколькими степенями свободы?

2. При каких условиях наблюдаются фигуры Лиссажу?

3. Можно ли наблюдать биения на экране осциллографа, подключив выход звукового генератора на Х-вход осциллографа, а контрольный сигнал  на Y-вход?

4. Как можно представить в виде колебаний равномерное движение точки по окружности?

ЛИТЕРАТУРА

1. Кембровский Г.С. Приближённые вычисления и методы обработки результатов измерений в физике. -Минск: Изд-во "Университетское", 1990. -189 с.

2. Матвеев А.Н. Механика и теория относительности. -М.: Высшая школа, 1986. -320 с.

3. Петровский И.И. Механика. -Минск: Изд-во БГУ, 1973. -352 с.

4. Савельев И.В. Курс общей физики. -М.: Наука, 1982. Т. 1. Механика. Молекулярная физика. -432 с.

5. Сивухин Д.В. Общий курс физики. М.:Наука, 1989 Т.1 Механика.-576 с.

6. Стрелков С.П. Механика. -М.: Наука, 1975. -560 с.

7. Физический практикум. Под ред. Кембровского Г.С. -Минск: Изд-во "Университетское", 1986. -352 с.

7