
Инерциальные_свойствава_твердого_тела.pdf_(182_Кб) / metod_mehanika / Инструкции к лабораторным работам / Механика старые / 20. Маятник Максвелла
.docРабота 20. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
И ПРОВЕРКА ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
ПРИ ПОМОЩИ МАЯТНИКА МАКСВЕЛЛА
Задание: определить момент инерции маятника Максвелла с предельной относительной погрешностью , не превышающей 5 %.
Рис.
1

ОПИСАНИЕ УСТАНОВКИ
Общий вид установки показан на рис. 1. На вертикальной стойке 3 основания 1 крепятся два кронштейна: верхний 4 и нижний 5. На верхнем кронштейне находится электромагнит 6, фотоэлектрический датчик 7 и устройство 8 для крепления и регулировки длины бифилярной подвески маятника. Нижний кронштейн вместе с прикрепленным к нему фотоэлектрическим датчиком 9 можно перемещать вдоль стойки и фиксировать в произвольно выбранном положении.
Маятник представляет собой диск 11, закрепленный на стержне 10, подвешенном на двух нитях. На диске крепятся сменные кольца. Маятник фиксируется в верхнем исходном положении с помощью электромагнита. На вертикальной стойке нанесена миллиметровая шкала, по которой определяется ход маятника.
ЭЛЕМЕНТЫ ТЕОРИИ
Рис.
2
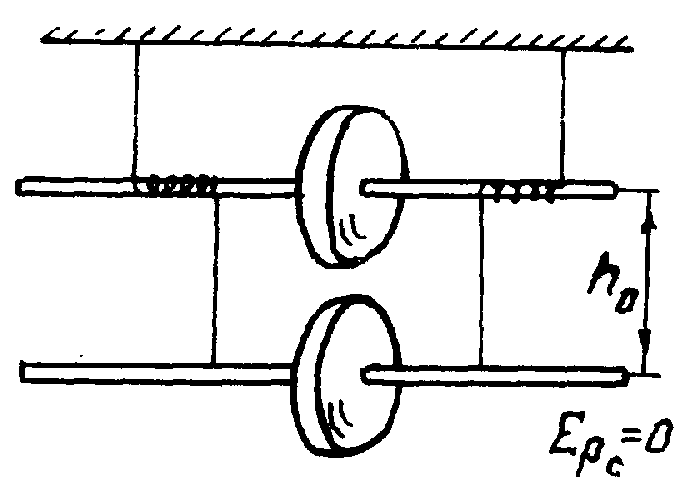
Рис.
3

![]() ,
приложенной в центре масс, и силы
натяжения нитей
,
приложенной в центре масс, и силы
натяжения нитей
![]() ,
приложенных к стержню в точках касания
нитей (силы трения не учитываем). Направим
ось X
вертикально
вниз, а ось Z
вдоль оси стержня. Тогда, по второму
закону Ньютона в проекции на ось X:
,
приложенных к стержню в точках касания
нитей (силы трения не учитываем). Направим
ось X
вертикально
вниз, а ось Z
вдоль оси стержня. Тогда, по второму
закону Ньютона в проекции на ось X:
![]() (1)
(1)
или
max = mg - 2T, (2)
где ax– проекция ускорения центра масс маятника, m – масса маятника.
Основное уравнение динамики вращательного движения маятника:
Mz = J (3)
где
![]() – проекция момента силы натяжения нитей
на ось вращения Z,
r0
– радиус стержня, Jz
– момент
инерции маятника относительно оси
вращения Z,
z
– проекция
углового ускорения маятника на ось Z.
При отсутствии проскальзывания
нерастяжимой нити
– проекция момента силы натяжения нитей
на ось вращения Z,
r0
– радиус стержня, Jz
– момент
инерции маятника относительно оси
вращения Z,
z
– проекция
углового ускорения маятника на ось Z.
При отсутствии проскальзывания
нерастяжимой нити
![]() (4)
(4)
С учетом (4) уравнение (3) примет вид
![]() (5)
(5)
Из (2) и (5) следует:
![]() (6)
(6)
При a = const и v0 = 0
![]() (7)
(7)
где t – время движения маятника, h – расстояние, пройденное маятником за это время. Из соотношений (6) и (7) находим
![]() (8)
(8)
Расчет момента инерции маятника Максвелла. Правильная форма элементов маятника Максвелла позволяет рассчитать его момент инерции.
Рис.
4

![]() ,
момент инерции диска J2=1/2
m2R12,
момент инерции кольца J3=1/2
m3(R12+R22).
Момент инерции маятника
,
момент инерции диска J2=1/2
m2R12,
момент инерции кольца J3=1/2
m3(R12+R22).
Момент инерции маятника
![]() (9)
(9)
где m1, m2, m3 – массы соответственно стержня, диска и кольца, а r0, R1 и R2 – их радиусы (рис. 4).
Закон сохранения энергии. Если пренебречь силами трения и сопротивления воздуха, то для системы маятник Максвелла - Земля будет выполняться закон сохранения полной механической энергии:
![]() (10)
(10)
где
v
= at = 2h/t,
![]() (11)
(11)
Соотношение (10) вытекает из законов динамики (см. Приложение 1).
Порядок выполнения задания
1. Измерение момента инерции
1. Установить кронштейн 5 в крайнее нижнее положение.
2. Надеть сменное кольцо на диск. Установить необходимую длину нитей так, чтобы нижняя кромка сменного кольца находилась на 4-5 мм ниже оптической оси фотодатчика.
3. С помощью регулировки опор 2 установить диск на бифилярном подвесе посредине фотодатчика 9. Ось маятника должна быть горизонтальной.
4. Нажать кнопку “сеть” на панели секундомера 12.
5.Накрутить нити на стержень 10 виток к витку и зафиксировать маятник в верхнем положении при помощи электромагнита 6.
6. Установить индикатор отсчета времени на 0, нажав кнопку “сброс”.
7. Нажать кнопку “пуск”. Происходит отключение электромагнита и включение секундомера в момент пересечения маятником оптической оси нижнего фотодатчика отсчет времени прекратится.
8. Вновь поднимающийся маятник в верхнем положении удержать рукой и осторожно опустить вниз.
9. Записать время падения маятника (отсчитав его по миллисекундомеру).
10. Проделать операции, обозначенные в пунктах 6-9 3-5 раз.
11. По формуле (8) вычислить момент инерции маятника.
12. Произвести измерения с каждым из сменных колец.
13. Оценить полную относительную погрешность косвенных измерений Jz.
2. Вычисление момента инерции
1. Измерить r0, R1 и R2 (рис. 4) штангенциркулем.
2. Определить массу элементов маятника (величина их нанесена на маятнике и на сменных дисках).
3. По формуле 9 рассчитать момент инерции маятника и оценить минимальную относительную погрешность косвенных измерений величины Jz.
4. Сравнить измеренный момент инерции с расчетным.
3. Проверка закона сохранения энергии
1. Вычислить v и по формулам (11).
2. Проверить выполнение (10), воспользовавшись полученными данными для m, Jz и h в одном из предыдущих опытов.
На основании проделанных измерений сформулировать цель работы и сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какую физическую величину называют моментом инерции?
2. Рассчитать момент инерции цилиндрического стержня.
3. В каком из сложных движений участвует маятник?
4. Какие точки маятника будут иметь одинаковое ускорение?
5. Выведите закон сохранения энергии из законов движения.
ЛИТЕРАТУРА
1. Кембровский Г.С. Приближённые вычисления и методы обработки результатов измерений в физике. -Минск: Изд-во "Университетское", 1990. -189 с.
2. Матвеев А.Н. Механика и теория относительности. -М.: Высшая школа, 1986. -320 с.
3. Петровский И.И. Механика. -Минск: Изд-во БГУ, 1973. -352 с.
4. Савельев И.В. Курс общей физики. -М.: Наука, 1982. Т. 1. Механика. Молекулярная физика. -432 с.
5. Сивухин Д.В. Общий курс физики. М.: Наука, 1989 Т. 1. Механика. -576 с.
6. Стрелков С.П. Механика. -М.: Наука, 1975. -560 с.
7. Физический практикум. Под ред. Кембровского Г.С. -Минск: Изд-во "Университетское", 1986. -352 с.
Приложение 1.
Закон сохранения энергии для замкнутой консервативной системы вытекает из законов движения. Из (2) с учетом (5) имеем
![]() или
или
![]() (12)
(12)
где
![]()
Умножив
уравнение (12) на
![]() ,
получим
,
получим
![]() (13)
(13)
Учитывая,
что
![]() получим
получим
 или
или
![]() (14)
(14)
Поскольку
при t
= tmax
![]() x
= h,
а при t
= 0 const
= 0, из (14) следует
(10):
x
= h,
а при t
= 0 const
= 0, из (14) следует
(10):
![]() (10)
(10)
