
- •2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил.
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении.
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
- •2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Векторные пространства. Линейная зависимость векторов. Базис. Размерность
- •3. Движение твердого тела вокруг одной неподвижной точки. Скорости и ускорения точек тела
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Линейные операторы и их матрицы. Собственные значения и собственные векторы. Нормальные формы матрицы линейного оператора
- •1. Кривые второго порядка. Их канонические уравнения
- •2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Поверхности второго порядка. Их канонические уравнения
- •2. Уравнения Лагранжа 2-ого рода
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
Опр:
Жидкость наз-ся идеальной, если на
площадке соприкосновения двух движущихся
объектов действуют лишь нормальные
силы давления. Касательные силы трения=0
в случае идеальной жидкости.
 -
по нормали.
-
по нормали.
Тензор
напряжений:


Уравнения движения идеальной жидкости и газа.
Так
как нет касательных напряжений, т.е.

 ;
;
 -коэф.
вязкости в уравнении Навье-Стокса:
-коэф.
вязкости в уравнении Навье-Стокса:
получаем уравнения Эйлера:
 -
замкнутая система
-
замкнутая система

 -уравнение
неразрывности
-уравнение
неразрывности
Уравнения Эйлера в декартовых координатах + уравнение неразрывности:

Интеграл Бернулли
Опр: Линии тока- линии, такие что в данный момент времени t касательная к линии совпадает с вектором скорости.(L)

 -
диф. уравнение линий тока.
-
диф. уравнение линий тока.
Предположим,
что выполняются условия: 1.движение
установившееся

2.внешние
силы потенциальны:
 3.условие
баротропии
3.условие
баротропии

Тогда
 ;
; ;
;
=> =>
=> -
интеграл Бернулли
-
интеграл Бернулли
где
 -
функция давления
-
функция давления
1.
ρ=const
=>
 ;
2.
;
2. =>
=>
Интеграл
Бернулли справедлив вдоль линий тока
или вихревых линий  -
вектор вихря.
-
вектор вихря.
Сопло Лаваля - газовый канал, суженный в середине, разгоняющий проходящий по нему газовый поток до сверхзвуковых скоростей.

Отношение
локальной скорости ![]() к
локальной скорости звука
к
локальной скорости звука![]() обозначается числом
Маха, которое также понимается местным,
то есть зависимым от координаты
обозначается числом
Маха, которое также понимается местным,
то есть зависимым от координаты![]() :
:![]()
*
При дозвуковой
скорости движения
газа (M
< 1), производная ![]() -
сопло сужается.
-
сопло сужается.
*
При сверхзвуковой
скорости движения
газа (M
> 1), производная ![]() -
сопло расширяется.
-
сопло расширяется.
* При
движении газа со
скоростью звука (M
= 1), производная ![]() -
площадь поперечного сечения достигает
экстремума,
то есть имеет место самое
узкое сечение сопла,
называемое критическим.
-
площадь поперечного сечения достигает
экстремума,
то есть имеет место самое
узкое сечение сопла,
называемое критическим.
3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
Плоско-параллельнымназывается такое движение тела, при
котором все точки тела движутся
параллельно некоторой неподвижной
плоскости. Из этого следует, что все
точки тела, лежащие на одном перпендикуляре,
проведенном в теле к этой плоскости,
движутся одинаково. Поэтому для изучения
плоскопараллельного движения тела
достаточно изучить только движение его
сечения. Движение сечения определяется
движением отрезкаCD,который
определяется положением точкиCи угла .
Тело имеет три степени свободы:
.
Тело имеет три степени свободы: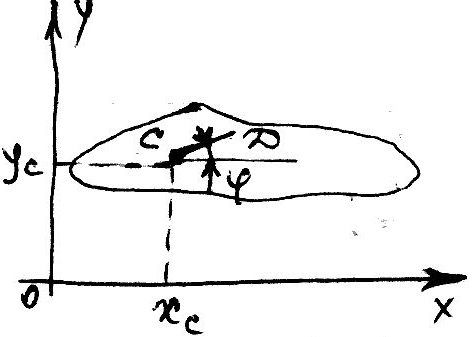
 - закон плоскопараллельного движения,
- закон плоскопараллельного движения,
точка С называется полюсом.
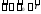 =>
=> =>
=>

 -
скорость полюса;
-
скорость полюса;
 ,
, - скорость точки М по отношению к системе
координат, которая имеет начало в точке
О` и неподвижной оси координат.
- скорость точки М по отношению к системе
координат, которая имеет начало в точке
О` и неподвижной оси координат.
 - формула Эйлера скорости и ускорения
точек, лежащих на одном перпендикуляре
одинаковы при плоско параллельном
движении.
- формула Эйлера скорости и ускорения
точек, лежащих на одном перпендикуляре
одинаковы при плоско параллельном
движении.
Мгновенный центр скоростей
Если известна скорость какой-нибудь точки фигуры и направление скорости другой её точки, то можно определить скорость любой точки плоской фигуры с помощью мгновенного центра скоростей (МЦС).
В данный
момент времени в данном положении эта
фигура вращается вокруг точки P,
то в этот момент распределение скоростей
будет именно таким, как если бы было
вращение вокругP.
Следовательно,

 ,
гдеMP– мгновенный радиус.
,
гдеMP– мгновенный радиус.

Недостаток: формула справедлива только в данный момент времени.
Рассмотрим случаи когда:
а)


если МЦС= ,
то
,
то
В этом
случае – мгновенно поступательное
движение
 ,
т.е скорости точек одинаковы
,
т.е скорости точек одинаковы
б)




 мгновенно-
поступательное движение
мгновенно-
поступательное движение

в) пара сил
г) Одно тело катится по поверхности другого без скольжения
МЦС – точка касания.
Ускорение: Пусть имеем плоскую фигуру, дана скорость одной из точек, ускорение, угловая скорость. ОпределитьWлюбой точки.




(*)
 ,
где
,
где
 - формула Эйлера
- формула Эйлера
 ,
т.к
,
т.к плоскости,
плоскости, ей),
то
ей),
то
(*)
 ,
обозначим
,
обозначим ,
, ,
тогда
,
тогда
 ,
,
Т.к
 и
и получим
получим
 ,
где
,
где
Если
 и
и направлены в одну сторону, то
направлены в одну сторону, то всегда
направлена от плоскости к полюсу.
Направление
всегда
направлена от плоскости к полюсу.
Направление зависит
от знака
зависит
от знака .
.
*![]() и
и![]() одинакового
знака *
одинакового
знака *![]() и
и![]() различных знаков
различных знаков

При непоступательном движении плоской фигуры в её плоскости на фигуре в любой момент времени существует точка, ускорение которой в любой момент времени равно 0. Эта точка называется мгновенным центром ускорений (МЦУ).


1)
 Провести под углом
Провести под углом к вектору
к вектору полупрямую, которая должна быть отклонена
от
полупрямую, которая должна быть отклонена
от![]() в
сторону вращения, если вращение ускоренное
и, в противном случае, замедленное.
в
сторону вращения, если вращение ускоренное
и, в противном случае, замедленное.
2) Отложим
по ней отрезок
 ,Q– мгновенный центр
скоростей.
,Q– мгновенный центр
скоростей.
Положим,
что
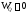 .
За полюс возьмём точкуA.
.
За полюс возьмём точкуA.
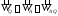


Правило
построения: выберем в качестве полюса
МЦУ точку Q, тогда ,
тогда
,
тогда


 ,
т.е при таком выборе полюса скорости
будут распределяться, т.к если бы вращение
шло было вокруг точкиQ.
,
т.е при таком выборе полюса скорости
будут распределяться, т.к если бы вращение
шло было вокруг точкиQ.
Мгновенный центр скоростей и мгновенный центр ускорений – различные точки, пример

Билет 3
