Variant_4 teor.v
..docx
Вариант 4
1. Монету бросают 5 раз. Найти вероятность того, что герб выпадет
1) хотя бы один раз;
2) не менее 2-х раз и не более 3-х раз.
Решение.
Опыт удовлетворяет схеме Бернулли.
Пусть успехом будет событие выпадения «герба» при одном бросании, тогда:
 ,
где n – количество
испытаний, m – количество
успехов.
,
где n – количество
испытаний, m – количество
успехов.
Согласно условию задачи:
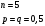
1) вероятность того, что "герб" выпадет хотя бы один раз.
![]()
2) вероятность того, что "герб" выпадет не менее 2-х раз и не более 3-х раз.

Ответ:
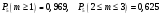 .
.
2. Из букв разрезной азбуки составлено слово "определение". Ребенок, не умеющий читать, рассыпал эти буквы и затем часть их собрал в произвольном порядке. Найти вероятность того, что
1) буква "е" появится раньше "о";
2) у него получится слово "деление".
Решение.
1) вероятность того, буква "е" появится раньше "о".
Т. к. в слове "определение" 4 буквы "е" и 1 буква "о", то используя классическое определение вероятности, получаем вероятность заданного события А:

2) вероятность того, что у него получится слово "деление".
Всего количество различных размещений из 11 букв по 7 равно:

В слове "определение" четыре буквы "е", в слове "деление" три буквы "е", следовательно, всего способов, которыми может быть составлено слово "деление", равно:
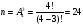 .
.
Используя классическое определение вероятности, получаем вероятность заданного события В:

Ответ:
 .
.
3. Группа студентов состоит из 5 отличников, 10 хорошо успевающих, 15 занимающихся слабо. Отличники на экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад два студента. Найти вероятность того, что
1) среди них окажется хотя бы один хороший студент;
2) были вызваны один слабый студент и один отличник, если они получили удовлетворительную и отличную оценки.
Решение.
1) вероятность того, что среди них окажется хотя бы один хороший студент.
Пусть А - событие, что среди выбранных окажется хотя бы один хороший студент.
Всего студентов 30, из них 20, либо отличники, либо занимаются слабо.
Число сочетаний из 30-ти студентов по 2 равно:

Число сочетаний из 20-ти студентов по 2 равно:
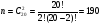
Используя классическое определение вероятности, получаем:

2) вероятность того, что были вызваны один слабый студент и один отличник, если они получили удовлетворительную и отличную оценки.
Пусть
В - событие, что студенты получили
удовлетворительную и отличную оценки,
 - события, что были вызваны, соответственно:
- события, что были вызваны, соответственно:
два занимающихся слабо;
один хорошо успевающий и один занимающийся слабо;
один отличник и один занимающийся слабо;
два хорошо успевающих;
один хорошо успевающий и один отличник;
два отличника.
Согласно условия:

Вероятность
события В, с учетом того, что событие
 произошло:
произошло:
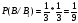
Вероятность
события В, с учетом того, что событие
 произошло:
произошло:

Вероятность
события В, с учетом того, что событие
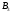 произошло:
произошло:
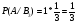

Используя формулу полной вероятности, получаем:

Ответ:
 .
.
4. Автомобиль едет по маршруту, на котором установлено 8 независимо работающих светофора. Каждый светофор с интервалом в 1.5 мин подает красный и зеленый сигналы. Найти среднее значение и стандартное отклонение числа остановок автомобиля на этой улице. Найти функцию распределения указанной случайной величины и построить ее график.
Решение.
Случайная величина Х может принимать значения: 0, 1, 2, 3, 4, 5, 6, 7, 8.
Опыт удовлетворяет схеме Бернулли.
Пусть успехом в схеме Бернулли будет событие, остановки автомобиля на одном светофоре:
 ,
где
,
где
 ,
а m – количество
успехов.
,
а m – количество
успехов.
Тогда:

Таким образом, закон распределения случайной величины Х:
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Р |
0,004 |
0,031 |
0,109 |
0,219 |
0,273 |
0,219 |
0,109 |
0,031 |
0,004 |
Математическое ожидание:
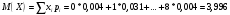
Дисперсия:

Среднеквадратическое отклонение:

Функция распределения выглядит следующим образом:

График функции распределения:

5. Рост женщины в некоторой местности является случайной величиной, распределенной по нормальному закону с дисперсией, равной 25 см2. Считая, что средний рост равен 168 см, найти вероятность того, что наугад выбранная женщина будет иметь рост
1) от 163 до 166 см;
2) более 166 см. Записать нормальный закон.
Решение.
Плотность распределения вероятностей нормально распределенной случайной величины, равна:

Параметры распределения:

Тогда:
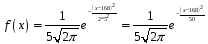
Функция распределения нормально распределенной случайной величины:
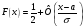 ,
где Ф – функция Лапласа.
,
где Ф – функция Лапласа.

1) вероятность того, что женщина будет иметь рост от 163 до 166 см.
Вероятность
попадания случайной величины распределенной
по нормальному закону в интервал
 равна:
равна:

2) вероятность того, что женщина будет иметь рост более 166 см.

Ответ:
 .
.
6. Задан закон распределения системы двух дискретных случайных величин (X, Y).
|
Y\X |
2 |
3 |
4 |
|
0 |
0,1 |
0,2 |
0,15 |
|
2 |
a |
0,15 |
0,25 |
6.1. Найти постоянную а.
6.2. Составить ряд распределения дискретной СВ X и построить полигон распределения.
6.3.
Вычислить вероятности событий А={Х<4}
и В={Х 4}.
4}.
6.4. Найти среднее значение СВ X.
6.5. Найти математическое ожидание функции СВ U=X-5X+3.
6.6. Найти степень разбросанности СВ X относительно ее среднего значения.
6.7. Найти дисперсию функции СВ U=X-5X+3.
6.8. Найти ковариацию СВ X и У. Что означает положительная ковариация?
6.9. Найти коэффициент корреляции СВ X и У. Может ли коэффициент корреляции равняться 2?
6.10. Найти коэффициент корреляции СВ X и V=-6+2X.
Решение.
6.1. Найти постоянную а.
Т.
к. сумма вероятностей возможных значений
пар равно единице, то:
равно единице, то:

6.2. Составить ряд распределения дискретной СВ X и построить полигон распределения.
Дополним таблицу данными законов распределения случайных величин X и Y:
|
Y\X |
2 |
3 |
4 |
PY |
|
0 |
0,1 |
0,2 |
0,15 |
0,45 |
|
2 |
0,15 |
0,15 |
0,25 |
0,55 |
|
PX |
0,25 |
0,35 |
0,4 |
|
Т. е. ряд распределения дискретной СВ X:
|
X |
2 |
3 |
4 |
|
PX |
0,25 |
0,35 |
0,4 |
Полигон распределения:

6.3.
Вычислить вероятности событий А={Х<4}
и В={Х 4}.
4}.
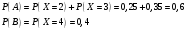
6.4. Найти среднее значение СВ X.

6.5. Найти математическое ожидание функции СВ U=X-5X+3.

6.6. Найти степень разбросанности СВ X относительно ее среднего значения.

6.7. Найти дисперсию функции СВ U=X-5X+3.

6.8. Найти ковариацию СВ X и У. Что означает положительная ковариация?

Положительная ковариация случайных величин означает, что отклонение одной из этих случайных величин в большую сторону от своего среднего значения вызывает отклонение другой случайной величины от ее среднего значения, также скорее в большую сторону, чем в меньшую.
6.9. Найти коэффициент корреляции СВ X и Y. Может ли коэффициент корреляции равняться 2?
Коэффициент корреляции СВ X и Y, равен:

Одно из основных свойств коэффициента корреляции:

Следовательно, коэффициент корреляции не может равняться 2.
6.10. Найти коэффициент корреляции СВ X и V=-6+2X.
Т. к. случайные величины Х и V линейно связаны, то:

Т.
к. в СВ V множитель перед
Х равен
 ,
то:
,
то:

7. Данные о месячной заработной плате 25 случайно отобранных рабочих завода приведены в таблице.
|
Зарплата, ден.ед. |
1700-1750 |
1750-1800 |
1800-1850 |
1850-1900 |
1900-1950 |
|
Число рабочих |
10 |
5 |
4 |
4 |
2 |
Вычислите выборочную среднюю зарплату и несмещенную оценку стандартного отклонения.
Решение.
Объем
выборки:
 .
.
Вычислим
середины интервалов
 :
:
|
Зарплата, ден.ед. |
1700-1750 |
1750-1800 |
1800-1850 |
1850-1900 |
1900-1950 |
|
|
1725 |
1775 |
1825 |
1875 |
1925 |
|
Число
рабочих
|
10 |
5 |
4 |
4 |
2 |
Выборочное среднее:
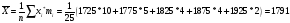
Несмещенная оценка стандартного отклонения:

8. Из 200 человек 95 поддерживают данного кандидата. Найти 95% доверительный интервал доли всех избирателей, поддерживающих данного кандидата. Сколько человек нужно опросить, чтобы с вероятностью 0,95 можно было утверждать, что доля избирателей, поддерживающих этого кандидата, отличается от истинной не более чем на 0,01?
Решение.
Считаем, что случайная величина Х – количество поддерживающих данного кандидата - распределена нормально.
Относительная частота количества, поддерживающих данного кандидата, равна:
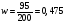
Доверительный
интервал, оценивающий долю р,
поддерживающих данного кандидата, в
генеральной совокупности с надежностью
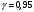 :
:
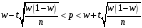
Параметр
t для надежности
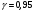 определим
из условия:
определим
из условия:
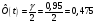 ,
где
,
где
 - табулированная функция Лапласа.
- табулированная функция Лапласа.
По таблицам определяем:

Тогда:

Величина отклонения доли всех, поддерживающих данного кандидата, от истинной, равна:

Тогда количество человек, которое нужно опросить, чтобы с вероятностью 0,95 можно было утверждать, что доля всех, поддерживающих данного кандидата, отличается от истинной не более чем на 0,01:

9. Производительность труда ткачих X и стаж работы Y характеризуется таблицей.
|
X, годы |
3 |
4 |
5 |
1 |
2 |
|
Y, м на 1 чел./ч |
13 |
21 |
22 |
12 |
17 |
Найдите уравнение зависимости между X и Y. Какую производительность труда можно предположить у ткачихи со стажем работы 7 лет?
Решение.
Уравнение линейной регрессии Y на X, ищем в виде:

Коэффициенты линии регрессии найдем из системы:

Используя формулы Крамера, получаем:

или

Находим соответствующие суммы:
|
|
|
|
|
|
|
1 |
3 |
13 |
9 |
39 |
|
2 |
4 |
21 |
16 |
84 |
|
3 |
5 |
22 |
25 |
110 |
|
4 |
1 |
12 |
1 |
12 |
|
5 |
2 |
17 |
4 |
34 |
|
|
15 |
85 |
55 |
279 |

В
итоге, получаем:
 .
.
Предполагаемая производительность труда у ткачихи со стажем работы 7 лет:
 (м на 1 чел./ч)
(м на 1 чел./ч)