Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусско-Российский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(Л4) Якимов_ДискретнаяМатематика_МУ

.pdf

Скачиваний:

Добавлен:

29.02.2016

Размер:

859.27 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Рисунок 7 – Элемент задержки

Предположим, что входной и, следовательно, выходной алфавиты есть X = {0, 1}; Y = {0, 1}. Тогда Q = {0, 1}. Под состоянием элемента задержки в момент времени t понимается содержание элемента памяти в данный момент. Таким образом, q(t) = x(t – 1), a y(t) = q(t) = x(t – 1).

Зададим элемент задержки таблицей 8, где а1 = 0, а2 = 1, q1 = 0, q2 = 1,

		δ(a1, q1) =δ(0, 0) =0;	λ(a1, q1) =λ(0, 0) =0 ;
		δ(a1, q2 ) =δ(0,1) =0 ;	λ(a1, q2 ) =λ(0,1) =1;
		δ(a2, q1) =δ(1, 0) =1;	λ(a2, q1) =λ(1, 0) =0 ;
		δ(a2, q2 ) =δ(1,1) =1;	λ(a2, q2 ) =λ(1,1) =1.
	Таблица 8 – Автоматная таблица элемента задержки

a			q
a		0		1
		0		1
0		δ = 0; λ = 0		δ = 0; λ = 1
1		δ = 1; λ = 0		δ = 1; λ = 1

Диаграмма Мура изображена на рисунке 8.

Рисунок 8 – Диаграмма Мура элемента задержки

Для представления этого автомата системой булевых функций используем таблицу автомата и вышеизложенный алгоритм. При этом кодирование производить не нужно, так как входной и выходной алфавиты и состояния уже закодированы.

Обратим внимание на то, что т = п = р = 2. Тогда k = r = s = l, и поэтому элемент задержки задается функциями δ и λ. Таблица истинности этих функций содержит 2k+r = 22 = 4 строки и k + r + r + s = 4 столбца.

Таблица 9 – Значения функций δ и λ элемента задержки

x	z	δ	λ
0	0	0	0
0	1	0	1
1	0	1	0
1	1	1	1

Канонические уравнения задаются следующими формулами:

z(t +1)	= x(t);	t =1, 2,...
		t =1, 2,...
y(t) = z(t).

Пример 2 – Схема сравнения на равенство.

Схема сравнения на равенство представляет собой устройство, сравнивающее числа x1 и х2, заданные в двоичной системе исчисления. Это устройство работает следующим образом. На вход устройства поступают по двум каналам числа x1 и х2. Число x1 является результатом сложения по модулю 2 байта данных, хранящегося в памяти компьютера. Число x2 является битом паритета, дополняющего число x1 так, чтобы их сумма сложения по модулю 2 была равна нулю. Это достигается при равенстве x1 и х2. Поэтому эти числа сравниваются устройством сравнения. При совпадении разрядов на выходе схемы формируется выходной сигнал 0, в противном случае на выходе появляется сигнал 1, что говорит о сбое в памяти. Ясно, что появление 1 в выходной последовательности означает, что сравниваемые числа x1 и х2 различны. Если же выходная последовательность является нулевой, то x1 = х2.

Для этого автомата X = {00; 01; 10; 11}; Y = {0,1}.

Функционирование схемы определяется двумя состояниями. Состояние q0 соответствует равенству сравниваемых в данный момент разрядов. При этом автомат остается в этом же состоянии. Если в следующий момент сравниваемые разряды будут различны, то автомат перейдет в новое состояние q1 и в нем остается. Так как это означает, что числа различны.

Таким образом, схему сравнения можно задать таблицей 10.

Таблица 10 – Автоматная таблица схемы сравнения

x			q
x	q0			q1
	q0			q1
00	q0;	0		q0;	1
01	q1;	1		q1;	1
10	q1;	1		q1;	1
11	q0;	0		q0;	1

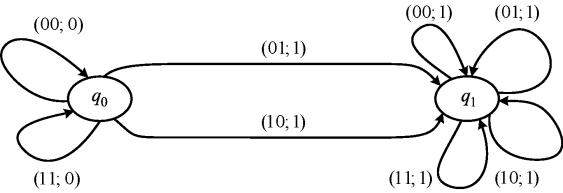
Диаграмма Мура схемы сравнения на равенство изображена на рисунке 9.

Рисунок 9 – Диаграмма Мура схемы сравнения на равенство

Кодирование состояний произведем следующим образом: α(q0) = 0; α(q1) = 1. Автомат будет задаваться функциями δ и λ (таблица 11).

Таблица 11 – Значения функций δ и λ схемы сравнения на равенство

x1	x2	z	δ	λ
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	1	1
1	0	0	1	1
1	0	1	1	1
1	1	0	0	0
1	1	1	1	1

Канонические уравнения задаются следующими формулами:

z(t +1)	= x1(t) x2(t) x1(t) x2(t) z(t);	t =1, 2,...
		t =1, 2,...
y(t) = x1(t) x2(t) x1(t) x2(t) z(t).

В качестве иллюстрации изложенного выше алгоритма задания канонических уравнений системой булевых функций рассмотрим пример 2 (см. таблицу 11).

Шаг 1. Строим СКНФ функции δ(x1, x2, z). Так как эта функция задана набором своих значений δ = (01111101), то ее СКНФ будет иметь следующий вид:

δ(x1, x2, z) = δ(x1, x2, z)=(x1 x2 z) (x1 x2 z) .

Шаг 2. Раскрываем скобки:

δ(x1, x2, z)=(x1 x2 z) x1 (x1 x2 z) x2 (x1 x2 z) =

= x1 x1 x2 x1 z x1 x1 x2 x2 x2 z x2 x1 z x2 z z z .

Упрощаем последнее выражение:

δ(x1, x2, z)=0 x1 x2 x1 z x1 x2 0 x2 z x1 z x2 z z =

= x1 x2 x1 x2 z(x2 x2 ) z(x1 x1) z = x1 x2 x1 x2 z .

Таким образом, получим

z(t +1) = x1(t) x2 (t) x1(t) x2 (t) z(t) .

Аналогично строится функция y(t). При этом из таблицы истинности (см. таблицу 11) выписываем набор значений функции λ = (01111101), который совпадает с набором значений функции δ(x1, x2, z).

3.4 Практические задания

Задание 1

Для автомата, заданного таблицей, постройте диаграмму Мура. Задайте этот автомат системой булевых функций.

1	x			q			5	x			q
1	x	0	1		2	3	5	x	0	1		2	3
		0	1		2	3			0	1		2	3
	0	(1; 1)	(3; 0)		(2; 0)	(2; 0)		0	(1; 0)	(3; 1)		(2; 0)	(1; 0)
	1	(2; 1)	(2; 0)		(3; 0)	(3; 0)		1	(3; 0)	(1; 1)		(0; 1)	(3; 1)

2	x			q			6	x			q
2	x	0	1		2	3	6	x	0	1		2	3
		0	1		2	3			0	1		2	3
	0	(0; 0)	(1; 1)		(3; 1)	(2; 0)		0	(2; 0)	(0; 0)		(3; 1)	(1; 0)
	1	(2; 0)	(0; 1)		(3; 1)	(1; 0)		1	(1; 0)	(0; 0)		(0; 0)	(3; 0)

3	x			q			7	x			q
3	x	0	1		2	3	7	x	0	1		2	3
		0	1		2	3			0	1		2	3
	0	(3; 0)	(2; 0)		(1; 1)	(0; 1)		0	(2; 1)	(2; 1)		(2; 1)	(2; 1)
	1	(0; 1)	(1; 1)		(2; 0)	(3; 0)		1	(1; 1)	(3; 1)		(0; 0)	(1; 0)

4	x			q			8	x			q
4	x	0	1		2	3	8	x	0	1		2	3
		0	1		2	3			0	1		2	3
	0	(1; 0)	(2; 0)		(2; 1)	(3; 0)		0	(0; 1)	(1; 1)		(2; 1)	(3; 1)
	1	(3; 0)	(3; 1)		(2; 1)	(1; 0)		1	(0; 0)	(0; 1)		(3; 1)	(2; 1)

												25

9	x						q						15
9	x	0			1			2			3		15
		0			1			2			3
	0	(0; 0)			(1; 1)			(2; 0)			(3; 1)
	1	(1; 0)			(0; 1)			(3; 0)			(2; 1)

10	x						q						16
10	x	0			1			2			3		16
		0			1			2			3
	0	(1; 1)			(0; 0)			(3; 1)			(2; 0)
	1	(0; 1)			(2; 0)			(2; 1)			(3; 0)

11	x						q						17
11	x	0			1			2			3		17
		0			1			2			3
	0	(0; 0)			(1; 1)			(2; 1)			(3; 1)
	1	(3; 1)			(0; 1)			(1; 1)			(2; 0)

12	x							q					18
12	x			0							1		18
				0							1
	0			(0; 0)					(0; 1)
	1			(0; 1)					(1; 0)
	2			(0; 1)					(1; 0)
	3			(1; 0)					(1; 1)

13	x							q					19
13	x			0							1		19
				0							1
	0			(0; 0)					(1; 1)
	1			(1; 0)					(1; 1)
	2			(0; 1)					(0; 0)
	3			(–; 1)						(–; 0)

14	x							q					20
14	x			1			2				3		20
				1			2				3
	0		(2; 0)			(2; 1)					(3; 1)
	1		(1; 1)			(3; 0)					(3; 1)
	2		(1; 1)			(2; 1)					(1; 0)

x						q
x		0			1			2		3
		0			1			2		3
0		(0; 0)		(0; 1)				(2; 0)		(2; 1)
1		(1; 0)		(1; 1)				(3; 0)		(3; 1)

x						q
x		0			1			2		3
		0			1			2		3
0		(0; 1)		(0; 0)				(1; 0)		(1; 0)
1		(2; 0)		(2; 1)				(3; 0)		(3; 1)

x						q
x		0			1			2		3
		0			1			2		3
0		(1; 0)		(3; 1)				(2; 1)		(2; 1)
1		(2; 1)		(2; 0)				(3; 0)		(3; 0)

	x							q
	x				0				1
					0				1
	0				(0; 0)				(1; 1)
	1				(1; 1)				(1; 1)
	2				(1; 1)				(1; 1)
	3				(0; 0)				(1; 1)

	x							q
	x				0				1
					0				1
	0				(0; 0)				(1; 1)
	1				(0; 0)				(0; 1)
	2				(1; 1)				(1; 1)
	3				(1; 1)				(0; 1)

x							q
x			1			2			3
			1			2			3
0			(1; 0)			(2; 1)			(0; 2)
1			(2; 1)			(2; 1)			(3; 0)
2			(3; 2)			(0; 1)			(2; 0)

Задание 2

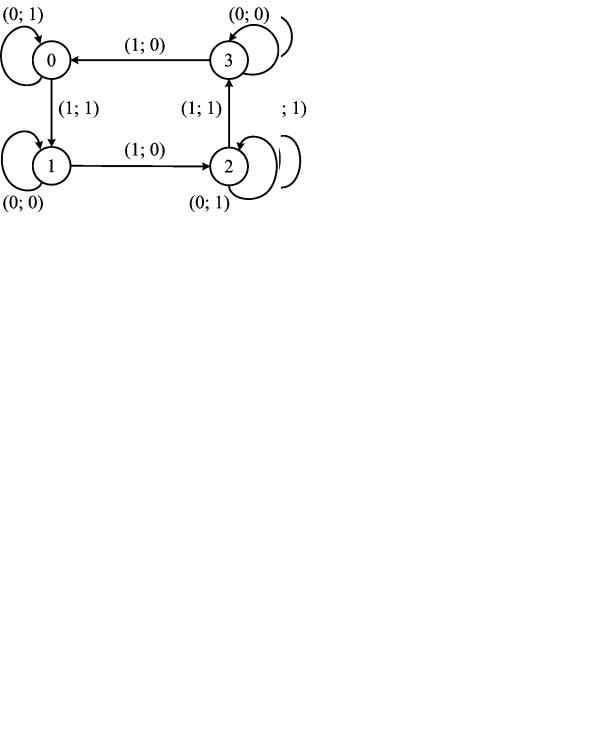
Для автомата, заданного диаграммой Мура, выпишите соответствующую таблицу и систему булевых функций (рисунки 10–25).

Рисунок 10

Рисунок 11

Рисунок 12

Рисунок 13

Рисунок 14

Рисунок 15

Рисунок 16

Рисунок 17

Рисунок 18

Рисунок 19

Рисунок 20

Рисунок 21

Рисунок 22

Рисунок 23

Рисунок 24

Рисунок 25

Задание 3

Для автомата, заданного каноническими уравнениями, постройте диаграмму Мура и соответствующую таблицу.

z(t +1) = x1(t) z(t) x2 (t) z(t);y(t) = x2 (t) z(t) x1(t) x2 (t).

z(t +1) = x(t);

y(t) = x(t) ↔ z(t).

z (t +1)			= x(t)	(z		(t) ↔ z					2	(t)) z				2	(t) x(t);
	1			1							2					2
z2 (t +1) = x(t) z2 (t) x(t) z1(t);
y (t) = x(t) (z				(t) z				2		(t)) x(t) z (t);
	1		1					2										1
y		(t) = x(t) z (t) z					2		(t) x(t) z									(t) z	2	(t).
	2		1				2									1			2
z (t +1)			= x(t)	(z	2	(t) z (t)) z								2	(t);
	1				2					1				2
z2 (t +1) = z1(t) [z2 (t) x(t) x(t) z2 (t)] z1(t) x(t);
y(t) = z			(t) x(t) z (t) z									2	(t) x(t).
		1				1						2

		(t +1) = z1(t) ↓ x(t);
	z1	(t +1) = z1(t) ↓ x(t);
5	z2 (t +1) = z1(t) → z2 (t);

	y(t) = x(t) z2 (t).
	z	(t +1) = z			(t) x(t);
6	1		2
6	z2 (t +1) = z1(t) x(t) z1(t) x(t);
	y(t) = z (t)		z			2	(t)	z (t) x(t).
		1				2			1
	z	(t +1) = z		(t) z				2	(t) x(t);
	1	1						2
7	z2 (t +1) = z2 (t) → x(t);

	y(t) = z2 (t) ↔ x(t).

z(t +1) = x1(t) x2 (t) x1(t) z(t) x2 (t) z(t);
				x2 (t) z(t).
y(t) = x1(t)				x2 (t) z(t).
z(t +1) = x1(t) x2 (t) x1(t) x2 (t) z(t);
				x2 (t) x1(t) x2 (t) z(t).
y(t) = x1(t)				x2 (t) x1(t) x2 (t) z(t).
z		(t +1) = x(t) z							2	(t)	z						(t) z			2	(t);
1									2							1				2
z2 (t +1) = z1(t) (z2 (t) x(t) x(t) z2 (t)) z1(t) x(t);
y	(t) = z (t)			x(t)					z			(t) z						2	(t) x(t).
			1							1								2
z		(t +1) = z		2	(t) x(t)						↔ z (t) x(t);
1				2													1
z2 (t +1) = z1(t) x(t) z1(t) x(t);
y	(t) = z (t)			z			2	(t) ↓ z					(t) x(t).
			1				2				1
z		(t +1) = z			(t) ↔ x(t);
1				2
z2 (t +1) = z1(t) x(t) z1(t) x(t);
y	(t) = z (t) \| z					2	(t)		z		(t) \| x(t).
			1			2				1
z		(t +1) = x(t) z							2	(t)	z						(t) z			2	(t);
1									2							1				2
z2 (t +1) = z1(t) (z2 (t) x(t) x(t) z2 (t)) z1(t) x(t);
y	(t) = z (t)			x(t)					z			(t) z						2	(t) x(t).
			1							1								2
z		(t +1) = x(t) z (t)									z					2	(t) x(t);
1								1								2
z2 (t +1) = x(t) z2 (t) x(t) z1(t);
y			(t) = x(t)	(z				(t) z					2		(t)) x(t) z (t);
1							1						2								1
y	2		(t) = x(t) z					(t) z				2		(t)			x(t)			z (t) z		2	(t).
	2						1					2									1	2


z1(t +1) = x(t) (z1(t) ↓ z2 (t)) z2 (t) x(t);
z	2	(t +1) = x(t) z	2	(t) ↓ x(t) z (t);
	2		2			1
y1(t) = x(t) (z1(t) z2 (t)) x(t) z1(t);
y		(t) = x(t) z (t) z			2	(t) x(t) z	(t) z	2	(t).
	2	1			2	1		2

Задание 4

По содержательному описанию работы автомата постройте автоматную таблицу, диаграмму Мура и систему булевых функций.

1 Двоичный сумматор последовательного действия представляет со-

бой устройство, осуществляющее сложение двух чисел в двоичной системе

исчисления. На входы сумматора подаются числа х1 и х2, начиная с младших разрядов. На выходе формируется последовательность, соответст-

вующая записи числа x1 + x2 в двоичной системе исчисления.

2 Схема сравнения на неравенство представляет собой устройство, позволяющее выяснить, равны ли сравниваемые x1 и x2, и если они не рав-

ны, выяснить, какое из них больше другого. Это устройство имеет два входа и два выхода. Выходные сигналы y1(t) и y2(t) определяются по следующим правилам:

y1(t) = y2(t) = 0, если x1(t) = x2(t);
y1(t) = 1; y2(t) = 0,	если x1(t) > x2(t);	т. е.	x1(t) = 1;	x2(t) = 0;
y1(t) = 0; y2(t) = 1,	если x1(t) < x2(t);	т. е.	x1(t) = 0;	x2(t) = 1.

3 Двоичные цифры 0 и 1 подаются на устройство, которое считает по модулю 3 накопленное число единиц (x – входные цифры, y – накопленное число).

4 Английский текст, составленный из 26 букв алфавита и пробелов, просматривается с целью подсчета числа слов, начинающихся с un и заканчивающихся на d (таких, как understand, united и др.). Для простоты пробелы обозначают буквой π, а все другие буквы, кроме d, n и u, – буквой λ.

5 Английский текст, составленный из 26 букв алфавита и проме-

жутков между буквами, просматривается с целью подсчета числа слов,

которые рифмуются с art (x – буква или промежуток, y – увеличение общего счета).

6 Построить конечный автомат, допускающий все цепочки в алфавите {a, b}, не содержащие вхождений подцепочки aba.

7 Построить конечный автомат, допускающий все цепочки в алфави-

те {a, b}, которые не начинаются с ab и не заканчиваются ab.

8 Построить конечный автомат, допускающий все последовательности нулей и единиц, кроме тех, которые содержат подпоследователь-

ность 11011.

9 Построить конечный автомат, допускающий те и только те цепочки в алфавите {0, 1}, которые не начинаются цепочкой 01 и не заканчиваются цепочкой 11 (т. е. не разрешаются цепочки вида 01x и цепочки вида y11,

каковы бы ни были цепочки x, y {0, 1}).

10 Найти конечный автомат с однобуквенными переходами, распо-

знающий язык {anbmck d | n ≥0, m ≥0, k ≥0}.

11 Найти конечный автомат с однобуквенными переходами, распознающий язык {anbm | n ≥3, m ≥3} .

12 Монета многократно подбрасывается и делается отметка при четных выпадениях цифры в последовательности цифр и при каждом втором (не обязательно подряд) выпадении герба (x – сторона монеты, y – отметка при броске).

13 Грузовой лифт, обслуживающий трехэтажный магазин, имеет кнопку вызова на каждом этаже и работает по следующим правилам: если нажата одна кнопка, то лифт движется на этаж, на котором расположена данная кнопка; если нажаты одновременно две или три кнопки, то лифт

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в папке Инд. задание к самостоятельной работе 2012 (ДМ РБ)

#
29.02.2016859.27 Кб46(Л4) Якимов_ДискретнаяМатематика_МУ.pdf
#
29.02.2016441.86 Кб63+Методические указания к ИЗ ДМ (теория и практика).doc