
- •Эконометрика
- •212000, Г. Могилев, пр. Мира, 43
- •1 Парная регрессия и корреляция
- •1.1 Расчетные формулы
- •1.2 Задание
- •2 Модели множественной регрессии
- •2.1 Расчетные формулы
- •2.2 Задание
- •3 Эконометрический анализ при нарушении классических
- •3.1 Теоретические положения
- •3.2 Задание
- •4 Методы и модели анализа временных рядов
- •4.1 Теоретические положения
- •4.2 Задание
- •Список литературы
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»
Кафедра «Автоматизированные системы управления»
Эконометрика
и экономико-математические
методы и модели
Методические указания
к лабораторным и практическим занятиям для студентов
специальностей 1-25 01 04 «Финансы и кредит»,
1-25 01 08 «Бухгалтерский учет, анализ и аудит»,
1-25 01 10 «Коммерческая деятельность»
Часть 1
Могилев 2012
У ДК
004.65
ДК
004.65
ББК 32.81
Э 11
Рекомендовано к опубликованию
учебно-методическим управлением
ГУ ВПО «Белорусско-Российский университет»
Одобрено кафедрой «Автоматизированные системы управления» «20» марта 2012 г., протокол № 7
Составитель: канд. техн. наук, доц. Т. В. Мрочек
Рецензент канд. техн. наук, доц. В. А. Широченко
Описаны основные этапы выполнения лабораторных и практических работ по первой части изучаемой дисциплины – эконометрике. Приведены основные понятия, расчетные зависимости и примеры выполнения наиболее распространенных задач по рассматриваемым темам.
Учебное издание
Эконометрика и экономико-математические методы
и модели
Ответственный за выпуск С. К. Крутолевич
Технический редактор А. Т. Червинская
Компьютерная верстка И. А. Алексеюс
Подписано в печать . Формат 60х84/16. Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл.-печ. л. . Уч.-изд. л. . Тираж 66 экз. Заказ №
Издатель и полиграфическое исполнение
Государственное учреждение высшего профессионального образования
«Белорусско-Российский университет»
ЛИ № 02330/375 от 29.06.2004 г.
212000, Г. Могилев, пр. Мира, 43
© ГУ ВПО «Белорусско-Российский
университет», 2012
1 Парная регрессия и корреляция
Цель: определение характеристик уравнений парной линейной и нелинейной регрессий, оценка значимости параметров и корреляции и выбор наилучшего уравнения регрессии.
1.1 Расчетные формулы
Регрессия – это модель вида
![]() ,
,
где y – зависимая переменная (результативный признак, функция отклика, эндогенная (внутренняя) переменная). Термин «внутренний» отражает тот факт, что значения зависимой переменной у определяются только значениями независимых переменных x;
х – независимая переменная (объясняющая переменная, фактор, входная переменная, внешняя или экзогенная переменная). Термин «внешний» говорит о том, что значения переменных х определяются вне рассматриваемой модели, для которой они являются заданными.
Знак «ˆ» («ридж») означает, что между переменными х и у нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина у складывается из двух слагаемых:
![]() ,
,
где у – фактическое (экспериментальное) значение результативного признака;
![]() –теоретическое
значение результативного признака,
найденное из уравнения регрессии;
–теоретическое
значение результативного признака,
найденное из уравнения регрессии;
![]() –случайная
величина, характеризующая отклонения
фактического значения у
от
–случайная
величина, характеризующая отклонения
фактического значения у
от
![]() .
.
Случайная величина i включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения [5, с. 44].
В
случае единственной входной переменной
![]() регрессию называютпарной
(простой),
если переменных
регрессию называютпарной
(простой),
если переменных
![]() две и более –множественной.
две и более –множественной.
В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию (экспоненциальную, логарифмическую и т. д.).
При изучении регрессии выполняют следующие этапы:
спецификация уравнения регрессии
 и определение параметров регрессии;
и определение параметров регрессии;
определение степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии;
проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов.
Спецификация
уравнения регрессии – это выбор вида
аналитической зависимости
![]() .
В случае парной регрессии спецификация
осуществляется по графическому
изображению реальных статистических
данных в виде точек в декартовой системе
координат, которое называется
корреляционным
полем
(диаграммой рассеивания) (рисунок 1.1).
.
В случае парной регрессии спецификация
осуществляется по графическому
изображению реальных статистических
данных в виде точек в декартовой системе
координат, которое называется
корреляционным
полем
(диаграммой рассеивания) (рисунок 1.1).
От правильно
выбранной спецификации модели зависит
величина случайных ошибок: они тем
меньше, чем в большей мере теоретические
значения результативного признака
![]() подходят к фактическим даннымy.
подходят к фактическим даннымy.
Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной х.
Простейшей является
линейная
взаимосвязь
между x
и y,
описываемая линейной функцией регрессии
вида
![]() .
.
Для вычисления
коэффициентов a,
b
используется метод
наименьших квадратов
(МНК), который позволяет получить
такие оценки параметров а
и b,
при которых
сумма квадратов отклонений фактических
значений зависимой переменной у
от теоретических ![]() минимальна, т. е.
минимальна, т. е.
![]()
Это означает, что линейная регрессия на диаграмме рассеивания будет проходить «достаточно близко» к точкам (xi, yi).
Теснота
связи изучаемых явлений оценивается
при использовании линейной регрессии
с помощью линейного
коэффициента корреляции
![]() .
.
Линейный коэффициент
корреляции
![]() принимает значение в пределах от (–1)
до 1, т. е. (–1) < rху
< 1. Чем ближе
принимает значение в пределах от (–1)
до 1, т. е. (–1) < rху
< 1. Чем ближе
![]() к единице,
тем связь теснее.
Качественная
оценка тесноты связи величин x
и y
может быть выявлена на основе шкалы
Чеддока.
к единице,
тем связь теснее.
Качественная
оценка тесноты связи величин x
и y
может быть выявлена на основе шкалы
Чеддока.
Линейный
коэффициент корреляции
характеризует
степень тесноты не всякой, а только
линейной зависимости. При нелинейной
зависимости между явлениями линейный
коэффициент корреляции теряет смысл,
и для измерения тесноты связи применяют
так называемый индекс
корреляции
![]() .
.
Для оценки
качества подбора линейной регрессии
рассчитывается квадрат линейного
коэффициента корреляции, называемый
коэффициентом
детерминации
![]() ,
а для нелинейной регрессии – квадрат
индекса корреляции, называемыйиндексом
детерминации
,
а для нелинейной регрессии – квадрат
индекса корреляции, называемыйиндексом
детерминации
![]() .
.
Коэффициент
детерминации характеризует долю
дисперсии
![]() результативного признакаy,
объясняемую регрессией, в общей дисперсии
результативного признакаy,
объясняемую регрессией, в общей дисперсии
![]() результативного признака. Чем больше
доля объясненной вариации, тем меньше
роль прочих факторов и тем лучше уравнение
регрессии описывает исходные данные.
Чем ближеR2
к 1, тем лучше
модель описывает (аппроксимирует)
исходные данные, и, значит, ее можно
использовать для оценки качества
построенной модели.
результативного признака. Чем больше
доля объясненной вариации, тем меньше
роль прочих факторов и тем лучше уравнение
регрессии описывает исходные данные.
Чем ближеR2
к 1, тем лучше
модель описывает (аппроксимирует)
исходные данные, и, значит, ее можно
использовать для оценки качества
построенной модели.
Средняя ошибка
аппроксимации
![]() – среднее
отклонение расчётных значений от
фактических. Построенное уравнение
регрессии считается хорошего качества,
если значение
– среднее
отклонение расчётных значений от
фактических. Построенное уравнение
регрессии считается хорошего качества,
если значение
![]() не превышает
8–10 % [5, с.
107].
не превышает
8–10 % [5, с.
107].
Средний коэффициент
эластичности
![]() показывает,
на сколько процентов в среднем изменится
результат у
от своей
средней величины при изменении фактора
х на
1 % от своего среднего значения:
показывает,
на сколько процентов в среднем изменится
результат у
от своей
средней величины при изменении фактора
х на
1 % от своего среднего значения:
![]() ,
,
где
![]() – первая
производная уравнения регрессии,
характеризующая соотношение приростов
результата у
и фактора х.
– первая
производная уравнения регрессии,
характеризующая соотношение приростов
результата у
и фактора х.
После того, как найдено уравнение линейной регрессии, проводится:
1) оценка значимости уравнения в целом с помощью F-критерия Фишера;
2) оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента.
F-критерий
Фишера дает
ответ на вопрос, при каких значениях R2
уравнение
регрессии следует считать статистически
незначимым, что делает необоснованным
его использование. Согласно F-критерию
Фишера, выдвигается «нулевая» гипотеза
Н0
о
статистической
незначимости уравнения регрессии (т.
е. о статистически незначимом отличии
величины F
от нуля).
Если расчетное значение F-критерия
![]() превышает табличное
превышает табличное
![]() ,
т. е.
,
т. е.
![]() ,
то гипотеза
Н0
отклоняется
и принимается статистическая значимость
и надежность уравнения регрессии. Если
,
то гипотеза
Н0
отклоняется
и принимается статистическая значимость
и надежность уравнения регрессии. Если
![]() ,
то гипотеза Н0
не отклоняется
и признается статистическая незначимость,
ненадежность уравнения регрессии.
,
то гипотеза Н0
не отклоняется
и признается статистическая незначимость,
ненадежность уравнения регрессии.
Табличное значение
F-критерия
![]() определяется
по таблицам F-критерия
Фишера при числе степеней свободы
определяется
по таблицам F-критерия
Фишера при числе степеней свободы
![]() m
(m
– число
параметров при переменных х),
m
(m
– число
параметров при переменных х),
![]() (n
– число наблюдений) и заданному уровню
значимости α.
(n
– число наблюдений) и заданному уровню
значимости α.
Уровнем значимости α в статистических гипотезах называется вероятность отвергнуть верную гипотезу. Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности отвергнуть верную гипотезу 5 и 1 %.
Возможна ситуация, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости, т. е. значения этих коэффициентов будут меньше их стандартной ошибки. В этом случае такие коэффициенты должны быть исключены из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии, наряду с проверкой значимости коэффициента детерминации R2, включает в себя также и проверку значимости каждого коэффициента регрессии.
Для оценки
статистической значимости коэффициентов
регрессии применяется t-критерий
Стьюдента,
согласно которому выдвигается «нулевая»
гипотеза Н0
о статистической
незначимости коэффициента уравнения
регрессии (т. е. о статистически
незначимом отличии a
и b
от нуля). Эта
гипотеза отвергается при выполнении
условия
![]() ,
при этом принимается статистическая
значимость и надежность проверяемого
коэффициента регрессии, т. е. считается,
что отличие рассматриваемого коэффициента
уравнения регрессии от нуля статистически
значимо. Табличное значениеt-критерия
,
при этом принимается статистическая
значимость и надежность проверяемого
коэффициента регрессии, т. е. считается,
что отличие рассматриваемого коэффициента
уравнения регрессии от нуля статистически
значимо. Табличное значениеt-критерия
![]() определяется
по таблице t-критерия
Стьюдента по числу степеней свободы
определяется
по таблице t-критерия
Стьюдента по числу степеней свободы
![]() и заданному уровню значимости α. Расчетные
значения
и заданному уровню значимости α. Расчетные
значения![]() -критерия
-критерия![]() для каждого коэффициента регрессии
(
для каждого коэффициента регрессии
(![]() -статистики
Стьюдента) представляют собой отношение
оценки коэффициента регрессии к его
стандартной ошибке.
-статистики
Стьюдента) представляют собой отношение
оценки коэффициента регрессии к его
стандартной ошибке.
Стандартные
ошибки коэффициентов
линейной регрессии позволяют получить
представление о точности полученных
оценок коэффициентов регрессии
![]() и
и![]() ,
о том, насколько далеко они могут
отклониться от истинных значений
коэффициентов.
,
о том, насколько далеко они могут
отклониться от истинных значений
коэффициентов.
Общая
дисперсия
![]() результативного
признака у
отображает
влияние как основных, так и остаточных
факторов. Остаточная
дисперсия
результативного
признака у
отображает
влияние как основных, так и остаточных
факторов. Остаточная
дисперсия
![]() результативного
признака у
отображает
влияние только остаточных факторов.
результативного
признака у
отображает
влияние только остаточных факторов.
Рассчитанные
значения оценок коэффициентов регрессии
являются приближенными, полученными
на основе имеющихся выборочных данных.
Для оценки того, насколько точные
значения оценок коэффициентов могут
отличаться от рассчитанных, осуществляется
построение доверительных интервалов.
Доверительные интервалы определяют
пределы, в которых лежит точное значение
определяемого показателя с заданной
вероятностью
![]() [1,
с. 131].
[1,
с. 131].
Доверительные интервалы для оценок коэффициентов линейной регрессии рассчитываются по формулам:
![]() ,
,
![]() ,
,
где
![]() ,
,![]() – предельные ошибки, рассчитываемые
по формулам
– предельные ошибки, рассчитываемые
по формулам
![]() ,
,
![]() .
.
В таблице 1.1 представлены формулы для вычисления основных характеристик линейной и различных нелинейных регрессий.
В MS Excel для построения функции линейной регрессии используются команда «Добавить линию тренда» и инструмент анализа «Регрессия».
Таблица 1.1 – Основные характеристики линейной и различных нелинейных регрессий
|
Функция у |
линейная
|
логарифмическая
|
степенная
|
экспоненциальная
| |
|
Среднеквадратические
ошибки
|
| ||||
|
Линейный
коэффициент корреляции
|
(–1) < rху< 1 |
–
| |||
|
Индекс корреляции
|
– |
| |||
|
Коэффициент детерминации |
|
– | |||
|
Индекс детерминации |
– |
| |||
|
Табличное
значение F-критерия
|
| ||||
|
Расчетное
значение F-критерия
|
| ||||
|
Средняя
ошибка аппроксимации
|
| ||||
|
Коэффициент
эластичности
|
|
|
|
| |
|
Общая
дисперсия
|
| ||||
|
Остаточная
дисперсия
|
| ||||
|
Стандартная ошибка коэффициента а |
| ||||
|
Стандартная ошибка коэффициента b |
| ||||
|
Расчетные значения
|
a |
| |||
|
b |
| ||||
|
Табличное
значение критерия Стьюдента
|
| ||||
Для построения функций линейной и нелинейной регрессий используется команда «Добавить линию тренда». На рабочий лист MS Excel вводятся исходные данные, после чего строится точечная диаграмма, представляющая собой поле корреляции (диаграмму рассеивания). Если щелкнуть правой кнопкой мыши на любой точке данных и в контекстном меню выбрать команду «Добавить линию тренда…», то появится диалоговое окно. В диалоговом окне на вкладке «Тип» необходимо щелкнуть по пиктограмме, например, «Линейная».
Далее необходимо открыть вкладку «Параметры» и в области «Название аппроксимирующей (сглаженной) кривой» выбрать опцию «автоматическое:». Следует убедиться, что опция «пересечение кривой с осью Y в точке:» не отмечена. Далее следует включить опции «показывать уравнение на диаграмме» и «поместить на диаграмму величину достоверности аппроксимации (R^2)» и щелкнуть на кнопке ОК. После этого необходимо выделить текст с уравнением регрессии и значением R2 и перетащить на свободное место диаграммы.
Построить линейное уравнение регрессии и выполнить расчет его характеристик можно с помощью режима Регрессия модуля Анализ данных
надстройки «Пакет анализа» процессора MS Excel следующим образом:
1) проверить доступ к пакету анализа. В главном меню выбирается Сервис/Надстройки и устанавливается флажок Пакет анализа;
2) в главном меню выбрать Сервис/Анализ данных/Регрессия;
3) заполнить диалоговое окно ввода данных и параметров вывода (рисунок 1.2).
В диалоговом окне режима Регрессия (см. рисунок 1.2) задаются следующие параметры.
Входные данные:
– Входной интервал Y – вводится диапазон адресов ячеек, содержащих значения уi (ячейки должны составлять один столбец);
– Входной интервал X – вводится диапазон адресов ячеек, содержащих значения независимых переменных. Значения каждой переменной представляются одним столбцом. Количество переменных – не более 16;
– Метки – флажок включается, если первая строка во входном диапазоне содержит заголовок. В этом случае автоматически будут созданы стандартные названия;
– константа-ноль – при включении этого параметра коэффициент а = 0;
– уровень
надежности. Данный
флажок устанавливается в активное
состояние, если в поле, расположенное
напротив флажка, необходимо ввести
уровень надежности, отличный от уровня
95 %, применяемого по умолчанию. Принятый
уровень надежности используется для
проверки значимости коэффициента
детерминации R2
и
коэффициентов регрессии
![]() .
.
Параметры вывода:
– Выходной интервал – при включении активизируется поле, в которое необходимо ввести адрес левой верхней ячейки выходного диапазона, который содержит ячейки с результатами вычислений режима Регрессия;
– Новый рабочий лист – при включении этого параметра открывается новый лист, в который, начиная с ячейки А1, вставляются результаты работы режима Регрессия;
– Новая рабочая книга – при включении этого параметра открывается новая книга, на первом листе которой, начиная с ячейки А1, вставляются результаты работы режима Регрессия.
остатки:
– остатки
– при
включении вычисляется столбец, содержащий
невязки
![]() ,
,![]() ;
;
– стандартизованные остатки – при включении вычисляется столбец, содержащий стандартизованные остатки;
– график
остатков –
при включении выводятся точечные графики
невязки
![]() ,
,![]() в зависимости
от значений переменных
в зависимости
от значений переменных
![]() .
Количество графиков равно числуm
переменных
.
Количество графиков равно числуm
переменных
![]() .
.
Далее рассмотрены показатели, объединенные названием Регрессионная статистика (см. ВЫВОД ИТОГОВ к примеру расчета) (рисунок 1.3).
Множественный
R
– коэффициент
корреляции
![]() .
.
R-квадрат – коэффициент детерминации R2.
Нормированный R-квадрат – приведенный коэффициент детерминации R2.
Стандартная ошибка – оценка s для среднеквадратического отклонения.
Наблюдения – число наблюдений п.
Далее рассмотрены показатели, объединенные названием Дисперсионный анализ (см. ВЫВОД ИТОГОВ к примеру расчета) (см. рисунок 1.3).
Столбец df
– это число
![]() степеней свободы, которое для строкиРегрессия
определяется
числом параметров при
переменных х
в уравнении
регрессии и равно т.
Для строки
Остаток число
степеней свободы определяется числом
наблюдений n
и количеством переменных в уравнении
регрессии т + 1:
степеней свободы, которое для строкиРегрессия
определяется
числом параметров при
переменных х
в уравнении
регрессии и равно т.
Для строки
Остаток число
степеней свободы определяется числом
наблюдений n
и количеством переменных в уравнении
регрессии т + 1:
![]() .
Для строкиИтого
число степеней
свободы определяется суммой чисел
.
Для строкиИтого
число степеней
свободы определяется суммой чисел
![]() и
и![]() .
.
Столбец SS – сумма квадратов отклонений. Для строки Регрессия – это сумма квадратов отклонений теоретических данных от среднего. Для строки Остаток – это сумма квадратов отклонений экспериментальных данных от теоретических. Для строки Итого – это сумма квадратов отклонений экспериментальных данных от среднего.
Столбец MS – дисперсии. Для строки Регрессия – факторная дисперсия, для строки Остаток – остаточная дисперсия.
Столбец F –
расчетное значение F-критерия
Фишера
![]() .
.
Столбец
Значимость
F
– значение
уровня значимости, соответствующее
вычисленному значению
![]() .
Определяется
с помощью функции = FРАСП(Fp;
df(регрессия);
df(остаток)).
Если
значимость
F
меньше уровня значимости α (обычно α =
0,05), то построенная регрессия является
значимой.
.
Определяется
с помощью функции = FРАСП(Fp;
df(регрессия);
df(остаток)).
Если
значимость
F
меньше уровня значимости α (обычно α =
0,05), то построенная регрессия является
значимой.
Столбец Коэффициенты – значения коэффициентов a, b.
Столбец Стандартная
ошибка – значения
![]() .
.
t-статистика – расчетные значения t-критерия.
Р-значение – значения уровней значимости, соответствующие вычисленным значениям tр. Определяются с помощью функции = СТЬЮДРАСП(tр; n–m–1). Если Р-значение меньше уровня значимости α, то принимается гипотеза о значимости соответствующего коэффициента регрессии.
Нижние 95 % и Верхние 95 % – соответственно нижние и верхние границы доверительных интервалов для коэффициентов регрессии.
Далее рассмотрены показатели, объединенные названием Вывод остатка (см. ВЫВОД ИТОГОВ к примеру расчета) (см. рисунок 1.3).
Столбец «Наблюдение» содержит номера наблюдений.
Столбец «Предсказанное
y»
содержит значения
![]() ,
вычисленные по построенному уравнению
регрессии.
,
вычисленные по построенному уравнению
регрессии.
Столбец «Остатки»
содержит значения невязок
![]() ,
которые вычисляются как разность между
эмпирическимиу
и теоретическими
,
которые вычисляются как разность между
эмпирическимиу
и теоретическими
![]() значениями результативного признакаy.
значениями результативного признакаy.
Пример – Зависимость доли расходов у на товары длительного пользования в общих расходах семьи в процентах от среднемесячных доходов х семьи (млн р.) представлена полем корреляций на рисунке 1.1, а [5, с. 85]. Построить уравнения линейной и логарифмической регрессий и выбрать регрессию, наилучшим образом описывающую исходные данные.
На основе рисунка 1.1, а можно выдвинуть гипотезу о том, что наилучшим образом описывать исходные данные будет, скорее всего, логарифмическая функция. Проверим это утверждение.
С помощью команды «Добавить линию тренда» на рисунке 1.1, б построены линии линейного и логарифмического трендов. Параметры полученных уравнений регрессий представлены в таблице 1.2.
По формулам, представленным в таблице 1.1, рассчитаны основные характеристики построенных регрессий. Результаты расчетов представлены таблицами 1.3 и 1.4.
Результаты построения линейного уравнения регрессии и расчета его характеристик с помощью режима Регрессия модуля Анализ данных надстройки «Пакет анализа» представлены на рисунках 1.3 и 1.4.
Сравнение результатов, полученных с помощью расчетных формул, с результатами применения инструментальных средств Excel показывает их близость, что свидетельствует о правильном понимании методики построения линейных регрессионных уравнений и оценки их качества.
а) б)


а – пары чисел
![]() ,
которые представляют собой поле
корреляции; б – графики линейной (1) и
логарифмической (2) регрессий
,
которые представляют собой поле
корреляции; б – графики линейной (1) и
логарифмической (2) регрессий
Рисунок 1.1 – Графики поля корреляций, линейной и логарифмической регрессий
Таблица 1.2 – Уравнения линейной и логарифмической регрессий
|
Функция
|
линейная
|
логарифмическая
|
|
a |
9,28 |
9,8759 |
|
b |
1,7771 |
5,1289 |
|
Уравнение
регрессии
|
|
|
Далее необходимо выбрать регрессию, наилучшим образом описывающую исходные данные.
Из расчетов видно,
что наименьшая остаточная дисперсия –
в логарифмической функции (![]() 0,0811).
0,0811).
Индекс корреляции
![]() = 0,9916превышает значение
линейного коэффициента корреляции
= 0,9916превышает значение
линейного коэффициента корреляции
![]() = 0,9742.
При этом 97%
вариации результативного признака y
логарифмической регрессии объясняется
вариацией фактора х,
а 3 % приходится на долю прочих факторов.
= 0,9742.
При этом 97%
вариации результативного признака y
логарифмической регрессии объясняется
вариацией фактора х,
а 3 % приходится на долю прочих факторов.
Наименьшая средняя
ошибка аппроксимации ![]() ,
задающая среднее отклонение расчетных
значений от фактических, содержится в
логарифмической регрессии:
,
задающая среднее отклонение расчетных
значений от фактических, содержится в
логарифмической регрессии:
![]() =1,3
(что не выходит за пределы интервала в
8–10 %).
=1,3
(что не выходит за пределы интервала в
8–10 %).
Таким образом,
наилучшим образом описывать исходные
данные будет логарифмическая регрессия,
что подтверждается значениями
![]() ,
,![]() ,
,![]() .
.

 Таблица
1.3 – Исходные данные к расчетам
Таблица
1.3 – Исходные данные к расчетам
|
Номер наблюдения i |
х |
y |
|
xy |
|
линейная |
|
|
логарифми-ческая |
|
|
|
1 |
1 |
10 |
1 |
10 |
100 |
11,0571 |
1,1175 |
10,5710 |
9,8759 |
0,0154 |
1,2410 |
|
2 |
2 |
13,4 |
4 |
26,8 |
179,56 |
12,8342 |
0,3201 |
4,2224 |
13,4310 |
0,0010 |
0,2312 |
|
3 |
3 |
15,4 |
9 |
46,2 |
237,16 |
14,6113 |
0,6220 |
5,1214 |
15,5106 |
0,0122 |
0,7180 |
|
4 |
4 |
16,5 |
16 |
66 |
272,25 |
16,3884 |
0,0125 |
0,6764 |
16,9861 |
0,2363 |
2,9458 |
|
5 |
5 |
18,6 |
25 |
93 |
345,96 |
18,1655 |
0,1888 |
2,3360 |
18,1305 |
0,2204 |
2,5239 |
|
6 |
6 |
19,1 |
36 |
114,6 |
364,81 |
19,9426 |
0,7100 |
4,4115 |
19,0657 |
0,0012 |
0,1798 |
|
Среднее значение |
3,5 |
15,5 |
15,1667 |
59,4333 |
249,9567 |
– |
– |
4,5565 |
– |
– |
1,3066 |
Т аблица
1.4 – Результаты расчетов
аблица
1.4 – Результаты расчетов
|
Функция
|
линейная
|
логарифмическая
| |
|
Среднеквадратическая
ошибка
|
| ||
|
Среднеквадратическая
ошибка
|
| ||
|
Линейный коэффициент корреляции
|
|
– | |
|
Индекс корреляции
|
– |
| |
|
Коэффициент детерминации |
|
– | |
|
Индекс детерминации |
– |
| |
|
Табличное значение
F-критерия
|
| ||
|
| |||
|
Функция
|
линейная
|
логарифмическая
| |
|
Расчетное значение
F-критерия
|
|
| |
|
Средняя ошибка
аппроксимации
|
|
| |
|
Коэффициент
эластичности
|
|
| |
|
Общая дисперсия
|
| ||
|
Остаточная
дисперсия
признака у |
|
| |
|
Стандартная ошибка коэффициента а |
|
| |
|
Стандартная ошибка коэффициента b |
|
| |
|
Расчетные значения
|
a |
|
|
|
b |
|
| |
|
Табличное значение критерия Стьюдента
|
| ||
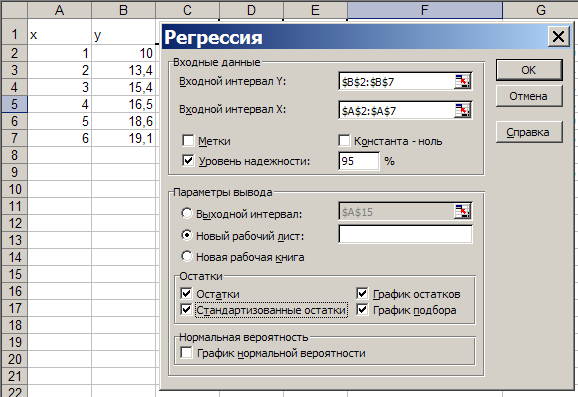
Рисунок 1.2 – Диалоговое окно режима Регрессия

Рисунок 1.3 – Вывод итогов к расчету




 Окончание таблицы 1.4
Окончание таблицы 1.4 

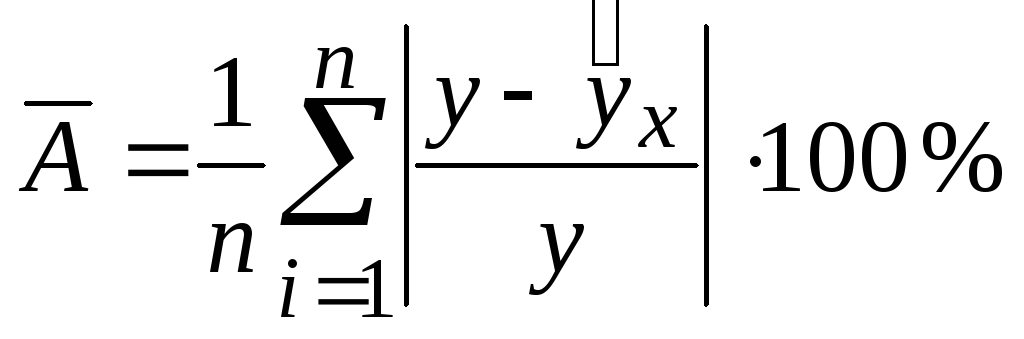 =4,5565
=4,5565 =0,0811
=0,0811


