6.2 Расчет размерной цепи теоретико- вероятностным методом
Согласно сборочному чертежу редуктора при сборке необходимо обеспечить зазор между торцом подшипника и крышкой, устанавливаемых на вал в пределах S = 0,…1,2 мм.
По сборочному чертежу вала выявляем все звенья размерной цепи А (А1…А8), участвующие в решении поставленной задачи. Вычерчиваем отдельно размерную цепь (рисунок 1). Выявленная размерная цепь содержит более пяти звеньев, в конструкции редуктора не предусмотрено использование детали, являющейся компенсатором, следовательно, в качестве метода достижения точности замыкающего звена принимаем метод неполной взаимозаменяемости.
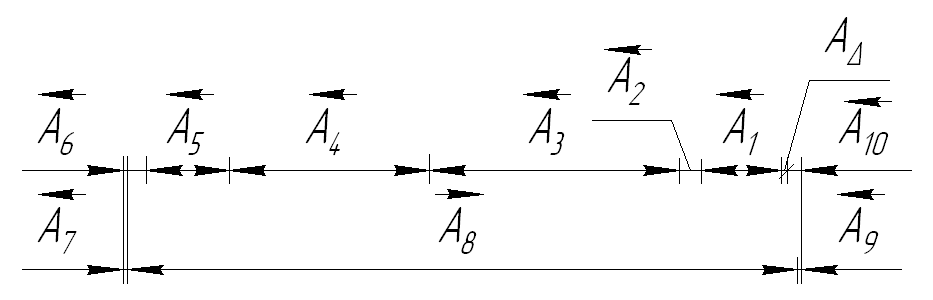
Рисунок 1 - Схема размерной цепи А
Размерная цепь – совокупность размеров образующих замкнутый контур и участвующих в решении поставленной задачи.
При расчете размерной цепи теоретико-вероятностным методом точность замыкающего звена обеспечивается не у всех изделий, а только у заранее обусловленной их части.
Метод основан на том, что при решении учитываются не предельные значения размеров, а вероятность их сочетания.
Достижение точности замыкающего звена методом неполной взаимозаменяемости предусматривает наличие заданного процента бракованных изделий после сборки. Рассчитаем размерную цепь А теоретико-вероятностным методом с процентом риска Р=1%. Расчет ведем согласно рекомендациям [5].
Исходные данные:
- замыкающее звено А = 0…1,2 мм;
- процент риска Р = 0,1 %;
- коэффициент риска t = 3,29;
- коэффициент, характеризующий закон рассеяния размеров 2i =1/9.
Записываем
параметры замыкающего звена в удобном
для дальнейшего расчета виде: А
=
,
Конструктивно по сборочному чертежу редуктора устанавливаем номинальные размеры составляющих звеньев.
А1 = мм; А2 = мм; А3 = мм; А4 = мм;
А5 = мм; А6 = мм; А7 = мм; А8 = мм;
А9 = мм; А10 = мм;
Размеры звеньев А1 и А5 равны ширине кольца подшипника (B = мм).
Проверяем правильность определения номинальных размеров составляющих звеньев по формуле
,
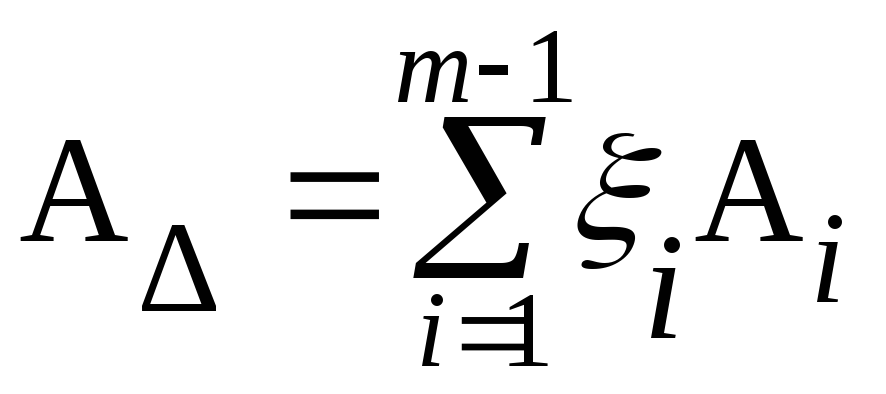АΔ= А7 + А8 + А9 – ( А 1 + А 2 + А 3 + А 4 + А5 + А 6 + А10) ;
АΔ = + + - ( + + + + + + ) = 0 мм.
Записываем параметры замыкающего звена:
- номинальный размер А = 0 мм;
- допуск замыкающего звена
ТА = ЕSА - EI А,
ТА = + - 0 = мм.
Определяем координату середины поля допуска замыкающего звена
,
мм.
Решаем задачу методом равных допусков. Для этого определяем среднюю величину допусков размеров составляющих звеньев по формуле
, 
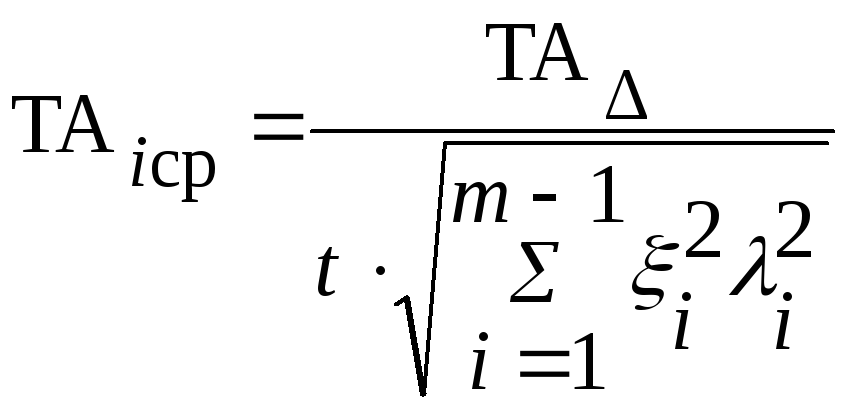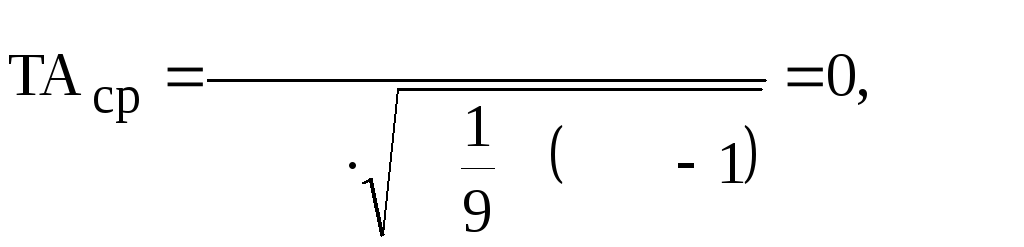мм.
Ориентируясь на полученное значение среднего допуска ТАcр = мкм для составляющих звеньев, учитывая их номинальные размеры назначаем стандартные допуски по ГОСТ 25.346-82 кроме звена А8 и А1, А5.
ТА2 = мкм; ТА6 = мкм; ТА3 = мкм; ТА8 = мкм;
ТА4 = мкм; ТА9 = мкм; ТА10 = мкм.
Для звеньев А1, А5 допуски выбираем из таблицы стандарта для подшипников ГОСТ 520-71 на ширину колец подшипника в зависимости от внутреннего диаметра и класса точности ТА1 = ТА5 = мкм;
Допуск на размер оставшегося звена А8 назначаем, используя формулу:
; 
ТА8 = мкм.
Для охватывающих звеньев допуск задается в «+», как для основного отверстия (Н), а для охватываемых в «-», как для основного вала (h). Для размеров деталей типа ступеней симметричное расположение отклонений в «±» (для звеньев А7, А10 - ступень крышки):
А1 = -0, мм; А2 = -0, мм; А3 = -0, мм; А4 = -0, мм; А5 = -0, мм; А6 = ± 0,0 мм; А7 = -0, ; А9 = -0, ; А10 = ± 0, мм.
Для определения координаты середины поля допуска звена А8 определим координаты середин полей допусков составляющих звеньев:
ЕсА1 = - мкм, ЕсА2 = - мкм, ЕсА3 = - мкм,
ЕсА4 = - мкм, ЕсА5 = - мкм, ЕсА6 = 0 мкм,
ЕсА7 = - мкм, ЕсА9 = - мкм, ЕсА10 = 0 мкм.
Координату середины поля допуска звена А8 найдем из выражения:
,
+
=
+
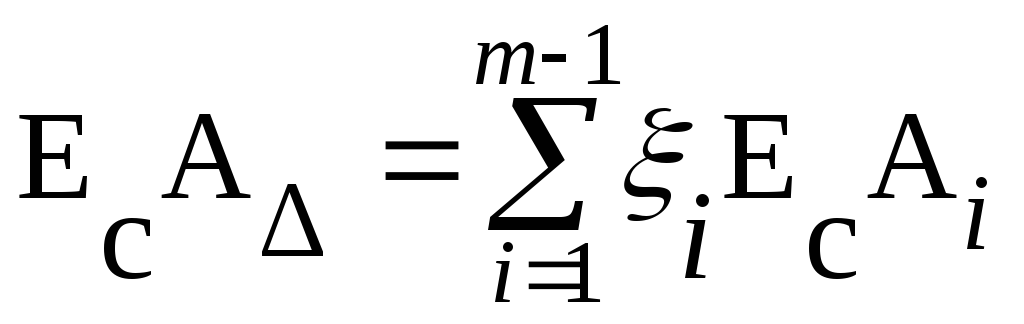(- ) + (- ) - (- - - - - - 0 - 0)
=
мкм.
Определяем предельные отклонения оставшегося звена
,
А8
мм.
Проведем проверку правильности расчетов размерной цепи.
Если расчеты размерной цепи выполнены правильно, тогда будут выполняться условия:
,
=
- + (- ) + (- )
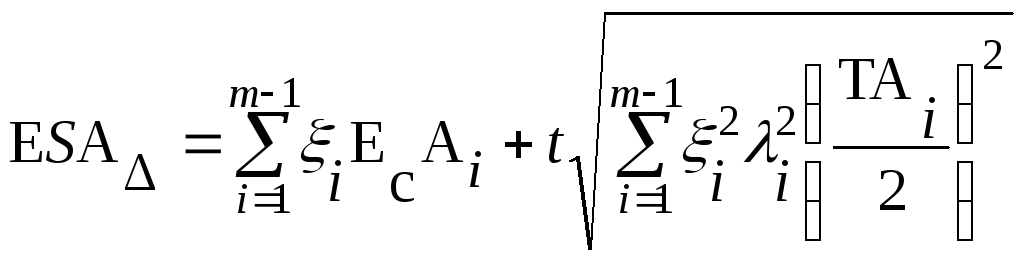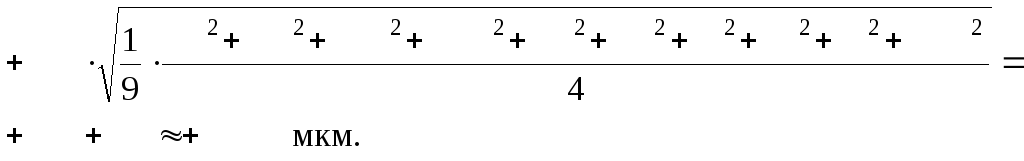
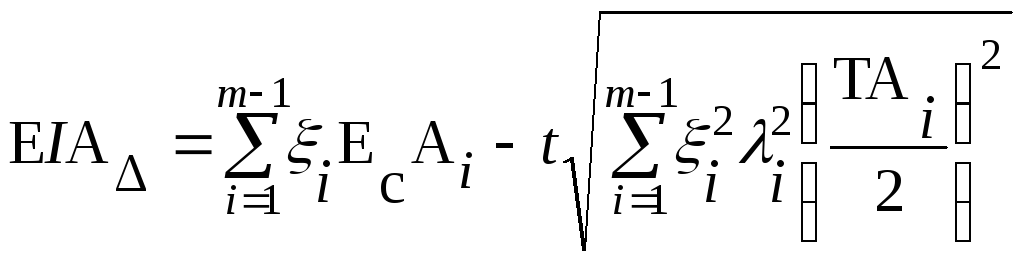- (- - - - - - 0 - 0) +
,
=
- + (- ) + (- )
- (- - - - - - 0 - 0) -
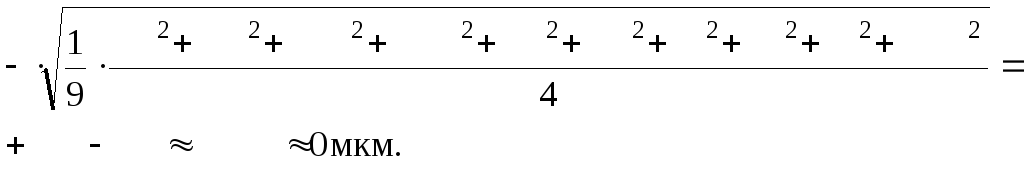
Так как расчетные ESA и EIA близки к исходным, то размерная цепь решена правильно.