2.2.8 Проверка зыбкости марша

Проверка зыбкости заключается в том, чтобы прогиб от непродолжительного действия груза N= 1кН (добавочного к полной нормативной нагрузке) не превышал 0,7 мм. При проверке используют значения, известные из предыдущего расчета и вычисляют дополнительные.

При кратковременном действии нагрузки в формуле по определению жёсткости следует учитывать модуль упругости бетонаи принимать соответствующее значение коэффициента(при кратковременном действии нагрузки= 1,0).Тогда жёсткость элемента при кратковременном действии нагрузки:

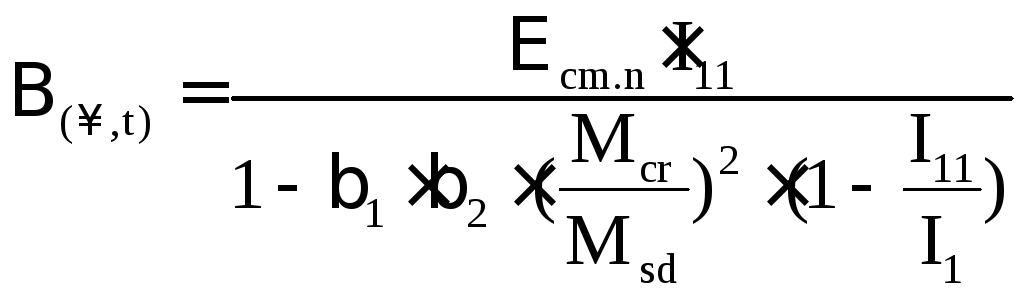, (2.30)

где - изгибающий момент, вызванный кратковременным действием нагрузкиМпа;

,

,

,

,

- при действии сосредоточенной нагрузки.

2.2.9 Расчет марша на монтажную нагрузку

При подъёме марша его вес передаётся на четыре петли, но при определённых условиях может возникнуть необходимость поднятия его за две петли, расположенные с одной стороны.

Собственный вес марша, согласно каталогу кг. Расчётный вес с учётом коэффициента динамичности:

Определяем нагрузку от собственного веса панели:

кН;

Усилие на одну петлю:

, (2.31)

кН.

Определяем площадь поперечного сечения одной петли из стали класса S240.МПа, (табл. [13]).

, (2.32)

мм².

Принимаем монтажную петлю диаметром 12 S240 мм².

2.3 Расчет железобетонной лестничной площадки

Необходимо рассчитать ребристую плиту лестничной площадки двухмаршевой лестницы 3000 мм.

Временная нормативная нагрузка 3 кН/м². Бетон класса C20/25. Арматура каркасов из стали класса S500, сеток из стали класса S500.

Рисунок 2.3 – План лестничной площадки

2.3.1 Определение нагрузок

Собственный нормативный вес плиты при h = 6 см:

Н/м².

Расчетный вес плиты:

Н/м².

Расчетный вес лобового ребра (за вычетом веса плиты):

H/м².

Расчетный вес крайнего пристеночного ребра:

H/м.

Расчетный вес поперечного ребра:

H/м.

Временная расчетная нагрузка:

кН∙м.

При расчете площадочной плиты рассмотрим раздельно полку, упругую заделанную в ребрах, лобовое ребро, на которое опираются марши, и пристеночное ребро, воспринимающее нагрузку от половины пролета полки плиты (рисунок 2.4).

Рисунок 2.4 – Сечение плиты

2.3.2 Расчет полки плиты

Полку плиты, при отсутствии поперечных ребер, рассматриваем как балочный элемент с частичным защемлением на опорах. Расчетный пролет равен расстоянию между ребрами м (рисунок 2.5).

Рисунок 2.5 – Расчетная схема

При учете образования пластического шарнира изгибающий момент в пролете и на опоре определяется по формуле, учитывающей выравнивание моментов:

, (2.33)

где Н/м – расчетная нагрузка;

Н∙м.

Вычисляем :

, (2.34)

гдеМПа – расчетное сопротивление бетона сжатию;

мм;

b = 1000 мм;

Подставляя полученные значения в формулу (2.34), получаем:

.

Находим по формуле

, (2.35)

где − коэффициент равный

−предельные относительные деформации бетона;

−относительные деформации арматуры;

−коэффициент равный .

Подставляя, получаем:

Сравниваем и:

;

тогда ;

.

Определяем площадь сечения продольной арматуры по формуле

, (2.36)

где МПа – расчетное сопротивление арматуры растяжению;

см² = мм².

Укладываем сетку С-1 из арматуры Ø4 S500 с шагом S = 200 мм на 1м длины с отгибом на опорах.