Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусско-Российский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

универ / Высш. математика. Определ. интеграл. Метод. указ. к практич

.pdf

Скачиваний:

Добавлен:

29.02.2016

Размер:

554.49 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»

Кафедра «Высшая математика»

ВЫСШАЯ МАТЕМАТИКА. МАТЕМАТИКА

Методические указания к практическим занятиям для студентов всех специальностей

ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ

Могилев 2014

УДК 517

ББК 22.1 В 93

Рекомендовано к опубликованию Центром менеджмента качества образовательной деятельности

ГУ ВПО «Белорусско-Российский университет»

Одобрено кафедрой «Высшая математика» «25» февраля 2014 г., протокол№5

Составители: ст. преподаватель Т. И. Червякова; доц. Л. И. Сотская

Рецензент А. В. Хомченко

Методические указания к практическим занятиям по теме «Определённые интегралы» предназначены для студентов всех специальностей.

Учебное издание

ВЫСШАЯ МАТЕМАТИКА. МАТЕМАТИКА

Ответственный за выпуск	Л. В. Плетнёв
Технический редактор	А. Т. Червинская
Компьютерная верстка	Н. П. Полевничая


Подписано в печать	. Формат 60×84/16. Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл. печ. л.		. Уч.-изд. л.	. Тираж 115 экз. Заказ №

Издатель и полиграфическое исполнение: Государственное учреждение высшего профессионального образования

«Белорусско-Российский университет». Свидетельство о государственной регистрации издателя, изготовителя, распространителя печатных изданий № 1/156 от 24.01.2014.

Пр. Мира, 43, 212000, Могилев.

Содержание

1Понятие определённого интеграла. Вычисление определённых интегралов.………….………………………..……………………………. 4

1.1 Теоретическая часть…………………………….…...…………… 4

1.2 Образцы решения примеров………………….……...................... 7

1.3 Примеры для самостоятельной работы……….……….…………8

1.4 Домашнее задание…………………………………………………9

2Замена переменной в определённом интеграле. Интегрирование по частям….…….…………………………………………………………... 10

2.1 Теоретическая часть…………………………….…….………….. 10

2.2 Образцы решения примеров………………….………………….. 10

2.3 Примеры для самостоятельной работы…………………………. 13

2.4 Домашнее задание…………………………….………………….. 14

3Геометрические приложения определённого интеграла………… 15 3.1 Теоретическая часть………………………………….…….…..… 15 3.2 Образцы решения примеров………….…………………………. 19 3.3 Примеры для самостоятельной работы………………………… 23 3.4 Домашнее задание………………….……………………………. 24

4Физические приложения определённого интеграла…….………. 25 4.1 Теоретическая часть…………………………………….…….….. 25 4.2 Образцы решения примеров……………………………….…….. 27 4.3 Примеры для самостоятельной работы…………………………. 31

4.4 Домашнее задание………………………………………………… 32

5 Несобственные интегралы.……….……………………………….. 33

5.1Теоретическая часть………………………….….……………….. 33

5.2Образцы решения примеров……………………….………….…. 35

5.3Примеры для самостоятельной работы……………….………… 38

5.4Домашнее задание………………………………………………… 39 Список литературы..……………..…………………………………… 40

				4
1 Понятие определенного интеграла. Вычисление
определённых интегралов
1.1 Теоретическая часть
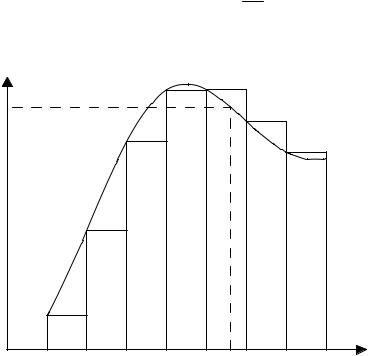
Пусть функция	y = f (x)		определена на отрезке [a;b] . Разобьем
произвольным образом этот отрезок точками a = x0 < x1 < x2 <... < xn =b на
n частичных отрезков длиной			xi	= xi − xi−1 , i =1, n . Выберем на каждом из
них точки ξi , xi−1 <ξi	< xi (рисунок 1.1).
y				y = f(x)
f(xi )
0	a	x1	x2	xi-1 ξi xi	b	x
Рисунок 1.1

Сумма вида Sn = ∑ f (ξi ) xi называется n -й интегральной суммой

i=1

функции y = f (x) на отрезке [a;b] .

Геометрически сумма Sn представляет собой алгебраическую сумму

площадей прямоугольников, в основании которых лежат частичные отрезки длиной xi = xi − xi−1 , а высоты их равны f (ξi ) .

Предел интегральной суммы Sn , найденный при условии, что длина

наибольшего частичного отрезка стремится к нулю, называется определённым интеграломотфункции y = f (x) впределахот x = a до x =b иобозначается

b	b		n
∫ f (x) dx ,	т. е. по определению ∫ f (x) dx = maxlimx →0		∑f (ξi )	xi .	Функция
a	a	i	i=1
a	a		i=1
y = f (x)	называется подынтегральной функцией,		f (x) dx	−	подынтег-

ральным выражением; [a;b] − отрезком интегрирования, a − нижним, b −

верхним пределом интегрирования.

Теорема. Если функция y = f (x) непрерывна на отрезке [a;b] , то она интегрируема на [a;b] , т. е. предел интегральной суммы Sn существует и

не зависит ни от		способа	разбиения отрезка [a;b] на частичные
отрезки	xi , ни от выбора на них точек ξi .
Если	f (x) ≥ 0 ,	x [a;b] ,	то геометрически определённый	интеграл
выражает площадь фигуры, ограниченной графиком функции				y = f (x) ,

осью 0x и прямыми x = a и x =b . Эта фигура называется криволинейной трапецией. В общем случае, когда функция y = f (x) на [a;b] принимает

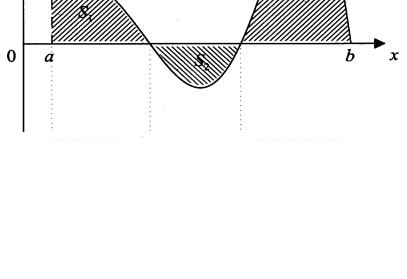
значения разных знаков, определённый интеграл выражает разность площадей криволинейных трапеций, расположенных над осью 0x и под ней. Например, для функции, график которой изображён на рисунке 1.2, имеем

∫b f (x) dx = S1 − S2 + S3 .

Рисунок 1.2

Перечислим основные свойства определённого интеграла:

− если функции	y = f (x)			и	y = ϕ(x) интегрируемы на
соответствующих отрезках, то
1) ∫b [f (x) ±ϕ(x)]dx = ∫b			f (x) dx ± ∫b ϕ(x) dx ;
a		a			a
2) ∫b c f (x) dx = c ∫b		f (x) dx		( c = const );

3) ∫b

f (x) dx = −∫a

f (x) dx ;

4) ∫b

f (x) dx = ∫c

f (x) dx + ∫b

f (x) dx ;

− если

f (x) ≥ 0 на [a;b] и a <b , то ∫b

f (x) dx ≥ 0 ;

− если ϕ(x) ≤ f (x) ,

x [a;b] , то ∫b ϕ(x) dx ≤ ∫b

f (x) dx ;

−

если

m = min f (x) ,

M = max f (x)

a <b ,

то

[a;b]

m (b −a) ≤ ∫b

f (x) dx ≤ M (b −a) ;

−

если функция y = f (x)

непрерывна на [a;b] ,

то на этом отрезке

существует хотя бы одна точка x = c , a ≤ c ≤b , такая, что верно равенство

	∫b	f (x) dx ≤ f (c) (b −a) ;
	a
− если функция y = f (x)			непрерывна на [a;b] и Φ(x) = ∫x			f (x) dx ,	то
					a
						x
′	− первообразная для y = f (x) . Φ(x) = ∫ f (x) dx						−
Φ (x) = f (x) , где Φ(x)	− первообразная для y = f (x) . Φ(x) = ∫ f (x) dx						−
интеграл с переменным пределом;						a
интеграл с переменным пределом;
− если F(x) −	какая-либо первообразная функции					f (x) ,	то
справедлива формула Ньютона-Лейбница:
∫b	f (x) dx = F(x)			ba = F(b) − F(a) .


a
a		0,			если f (x) −нечетная функция;
a			a

Замечание – ∫ f (x) dx =
−a		2	∫ f (x) dx,		если f (x) −четная функция.
			0

1.2 Образцы решения примеров

1.2.1 Вычислить определённый интеграл ∫2																																	3(x −1)2 dx .
Решение																														1
Решение
∫2 3(x −1)2 dx =3 ∫2 (x −1)2 dx =3 (x −1)3																											2		= (x −1)3							12 = (2 −1)3 −(1 −1)3 =1.
																											2

1						1																		3			1
1						1																					1
1.2.2 Вычислить ∫8 (																2x + 3			x )dx .
Решение												0
Решение
8															8									8									8		1					8	1
	∫(		2x + 3 x )dx = ∫ 2x dx + ∫3 x dx = 2 ∫x																																			dx + ∫x				dx =
	∫(		2x + 3 x )dx = ∫ 2x dx + ∫3 x dx = 2 ∫x																																		2	dx + ∫x			3	dx =
0															0									0									0							0
		x		3	8		x			4	8				2 2				3							3				4					2 2 16 2								3
					8						8

				2						3
= 2				2						3								82 −0											83 −0															16 =
						+						=												+									=									+
			3			+						=												+									=									+
			3					4							3											4													3				4
		2			0	3					0				3											4													3				4
															=		64		+		48			=	100				= 33			1		.


																	3
																	3		4							3				3
												π
1.2.3 Вычислить ∫4 sin 2x dx .
Решение												0
Решение
	π																	π
4												1						π					1					π											1				1
4												1			cos 2x			4					1					π											1	(0 −1)=			1
	∫sin 2x dx = −														cos 2x				= −					cos						−cos0						= −				(0 −1)=					.
0												2						0					2					2											2				2
0												2						0					2					2											2				2
												0				dx
1.2.4 Вычислить												−∫1				dx						.
1.2.4 Вычислить												−∫1		x2 + 2x + 2								.
Решение
0			dx								0				d(x +1)																0															π
−∫1			dx								−∫1				d(x +1)					= arc tg(x											0															π
									=																				+1)		−1			= arc tg1 −arc tg 0 =												4 .
	x2 + 2x + 2								=				(x +1)2 +1																					= arc tg1 −arc tg 0 =
	x2 + 2x + 2												(x +1)2 +1

1.2.5Вычислить ∫2 2x −1 dx .

1x3 + x

Решение

Разложим подынтегральную функцию на простейшие дроби:

2x −1

A Bx +C

Ax2

+ A + Bx2

+Cx

;

+ x2 +1 =

x(x2 +1)

A + B = 0,

C = 2,

A = −1,

Откуда A = −1, B =1,

C = 2 .

2 2x −1

2 dx

x + 2

2 dx 1

2 2x dx

∫1

dx = −∫1 x

+ ∫1

= −∫1 x

+ 2

∫1 x2 +1

+2∫1

x3 + x

x2 +1

ln (x

ln 5

−

ln 2 + 2arctg 2

−

= −ln | x | +

+1)+ 2arctgx

= −ln 2 +

−2arctg1 = 1 ln 5							−ln 2 + 2arctg 2 −2 π = ln				5	+ 2arctg 2 −	π	≈ 0,38.
−2arctg1 = 1 ln 5							−ln 2 + 2arctg 2 −2 π = ln				2	+ 2arctg 2 −	2	≈ 0,38.
				2		2			4	2	2		2
1.3 Примеры для самостоятельной работы
Вычислить определённые интегралы.
1.3.1	2			2x2 +		2	dx .		Ответ:	21 .
1.3.1				2x2 +		4	dx .		Ответ:	21 .
	∫1					x				4
1.3.2	∫4			x dx .					Ответ:	14 .
	1									3
	1			dx
1.3.3	∫0			dx				.	Ответ: arctg3 −arctg 2 ≈ 0,14 .
1.3.3	∫0		x2 + 4x +5					.	Ответ: arctg3 −arctg 2 ≈ 0,14 .
1.3.4	∫9			x −1		dx .			Ответ: 2 .
1.3.4	∫9			x +1		dx .			Ответ: 2 .
	4			x +1
		3		dx						π
1.3.5	∫				.				Ответ:	6 .
1.3.5	∫			x2 +1	.				Ответ:	6 .
		3

1		2
1.3.6 ∫0	x dx		.
	x2 +1
1.3.7 ∫7		3 1 + x2 x dx .
0
π
1.3.8 ∫2		cos x −cos3 x dx .
0
1.3.8 ∫2		x3 dx		.
		4
0		x + 4

Ответ: 4 −4 π. Ответ: 458 .

Ответ: 23 .

Ответ: 5 −1.

1.3.10 ∫e	1 +ln x dx .	Ответ: 1,5 .
1	x

1.3.11 ∫π sin2 x dx .

−π 2

2ex

1.3.12∫1 x2 dx .

1.3.13∫3 f (x) dx , если

0
1.3.14 ∫5	dx		.
1.3.14 ∫5	5 + 4x − x	2	.
2	5 + 4x − x

		Ответ: 1.
		Ответ: e −		e .
	3x	2	при 0	≤ x ≤1,	Ответ:17 .
f (x) =
2x +4			при1 < x ≤ 3.

Ответ: π2 .

1.4 Домашнее задание

Вычислить определённые интегралы.

	0,5		x dx						3
1.4.1	∫		x dx		.	Ответ: 1 −			3	.
									2
			2
	0		1− x
1.4.2	e	ln2 x		dx .		Ответ:	1	.
1.4.2	∫		x	dx .		Ответ:	3	.
	1		x				3
1.4.3	∫8		x +1 dx .			Ответ:	38 .
	3						3
	π
1.4.4	∫2 ctg3xdx .					Ответ: 0 .
	π
	6
	π
1.4.5	∫2 cos3 x sin x dx .					Ответ: 0,25 .

						10
	π
1.4.6	∫2	dx		.		Ответ: 0,5.
1.4.6	∫2			.		Ответ: 0,5.
	π	1 −cos 2x
	4
1.4.7	∫1	x3 5x4 + 4 dx .				Ответ:	19 .
	0						30
	1	dx						2 +	5
	∫0	dx						2 +	5
1.4.8					.	Ответ:	ln	1 +	2	.
1.4.8		x2 +	2x + 2		.	Ответ:	ln			.
		x2 +	2x + 2

2 Замена переменной в определённом интеграле. Интегрирование по частям

2.1 Теоретическая часть
Пусть функция y = f (x)		непрерывна	на	отрезке [a;b] . Функция
x = ϕ(t)				′
x = ϕ(t)	определена и непрерывна вместе со своей производной ϕ				(t) на
отрезке	[α;β], причем для любого t [α;β]			ϕ(t) [a;b] . Тогда,	если
ϕ(α) = a , ϕ(β) =b , то
	b	β
	∫ f (x) dx = ∫ f (ϕ(t))		′		(2.1)
	∫ f (x) dx = ∫ f (ϕ(t))		ϕ (t) dt .		(2.1)
	a	α

Это формула замены переменной для определенного интеграла. Пусть функции u(x) и v(x) имеют непрерывные производные на

отрезке [a;b] . Тогда справедлива формула интегрирования по частям:

b b

∫u dv =u v ba − ∫v du .

a a

2.2 Образцы решения примеров

2.2.1 Вычислить определённый интеграл ∫8	x dx		.

3	1 + x
Решение
Применим подстановку t = 1 + x . Тогда x +1 =t		2 ,

При x =3 t = 2 , а при x =8 t =3 .

(2.2)

x =t2 −1, dx = 2t dt .

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в папке универ

#
29.02.2016327.15 Кб16Высш. матем. Системы дифференц. уравнений.pdf
#
29.02.2016399.48 Кб43Высш. матем. Теория вероятностей Ч.1.pdf
#
29.02.2016885.22 Кб34Высш. матем. Теория вероятностей. Ч.2.pdf
#
29.02.2016792.51 Кб32Высш. матем.Метод. указ. и вариан.индив. зад.всех спец.2011.pdf
#
29.02.2016911.73 Кб20Высш. матем.Метод. указ. к контр. раб.№1 ст. технич. спец.заочн.2011.pdf
#
29.02.2016554.49 Кб15Высш. математика. Определ. интеграл. Метод. указ. к практич.pdf
#
29.02.2016404.98 Кб18Высш. математика. Ряды.pdf
#
29.02.2016345.15 Кб23Высш. математика. Тестовые задания.pdf
#
29.02.2016408.42 Кб18Высш.мат.ДУ.Метод.указ.к практ.зан.pdf
#
29.02.2016428.43 Кб17Высш.мат.Интегралы.Метод.указ.и вар.индив.зад.pdf
#
29.02.2016986.77 Кб22Высш.мат.Кратные интегралы.pdf