Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусско-Российский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

универ / Функция нескольких переменных.Метод. указ. к практ. занятиям

.pdf

Скачиваний:

Добавлен:

29.02.2016

Размер:

393.07 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»

Кафедра «Высшая математика»

ВЫСШАЯ МАТЕМАТИКА

Методические указания к практическим занятиям для студентов всех специальностей дневной и заочной форм обучения

Функции нескольких переменных

Могилев 2008

УДК 517.9 ББК 22.1

В 93

Рекомендовано к опубликованию учебно-методическим управлением

ГУ ВПО «Белорусско-Российский университет»

Одобрено кафедрой «Высшая математика» «31» июня 2008 г., протокол № 9

Составитель канд. физ.-мат. наук, доц. В. В. Пугин

Рецензент д-р техн. наук, проф. В. А. Ким

В методических указаниях к практическим занятиям по теме «Функции нескольких переменных» весь программный материал разделен на шесть частей – тем практических занятий с перечнем основных понятий и теоретических вопросов для усвоения, образцами решения и оформления примеров и задач, заданий для самостоятельной работы, рекомендуемой литературы.

Методические указания рекомендованы студентам всех специальностей и форм обучения в вузе и могут быть полезны также молодым преподавателям кафедры «Высшая математика».

Учебное издание

ВЫСШАЯ МАТЕМАТИКА

Ответственный за выпуск		Л. В. Плетнёв
Технический редактор		И. В. Русецкая
Компьютерная вёрстка		Н. П. Полевничая
Подписано в печать	. Формат 60х84/16. Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл.-печ. л.	. Уч.-изд. л.	. Тираж 99 экз. Заказ №

Издатель и полиграфическое исполнение Государственное учреждение высшего профессионального образования

«Белорусско-Российский университет» ЛИ № 02330/375 от 29.06.2004 г. 212000, г. Могилёв, пр. Мира, 43

Содержание

1 Понятие функции нескольких переменных. Предел и непрерывность функции нескольких переменных……………………... 4

2 Частные производные функции нескольких переменных, дифференцируемость функции нескольких переменных. Дифференциал функции нескольких переменных……………………………... 7

3 Дифференцирование сложных функций нескольких переменных, дифференцирование неявных функций………………….. 9

4 Производная по направлению. Градиент функции нескольких переменных. Касательная плоскость и нормаль к поверхности….. 13

5 Частные производные и дифференциалы высших порядков. Экстремум функции нескольких переменных…………………….. 17

6 Условный экстремум функции нескольких переменных. Наименьшие и наибольшие значения функции нескольких переменных в замкнутой области. Геометрическое решение задач

линейного программирования…………………………………………… 20

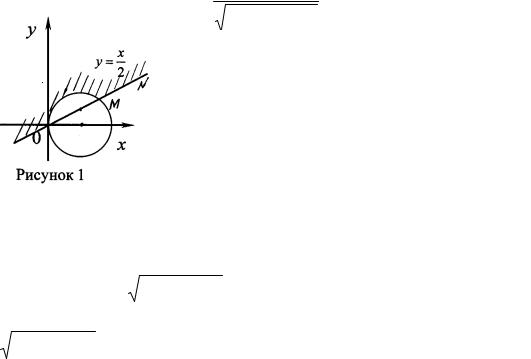
Список литературы………………………………………………… 24

1 Понятие функции нескольких переменных. Предел и непрерывность функции нескольких переменных

1.1 Основные понятия, теоретические вопросы

1Определение функции одной переменной, двух и трех переменных, определение функции n-переменных, примеры.

2Способы задания функции n-переменных.

3Геометрический смысл функции двух переменных.

4Линии уровня, поверхности уровня функции нескольких переменных (ФНП).

5Область определения и как ее найти для ФНП.

6Предел функций двух и трех переменных в точке Мо.

7Частные приращения и полное приращение ФНП.

8Непрерывность ФНП в точке и в области.

9Точки разрыва, линии, поверхности разрыва ФНП.

Рекомендуемая литература: [1, С. 117–124; 5, С. 243–251].

1.2 Образцы решения примеров и задач

1.2.1 Для функции z = ln(2 y − x) −	1	найти область опреде-
	x2 − 4x + y2

ления.

Решение

D(z) = {(x, y) R / 2 y − x > 0, x2 − 4x + y2 > 0}.
2
2 y − x > 0,			x
		y >		,
	или	y >	2	,
	или		2
x2 − 4x + y2 > 0					2	+ y	2	> 4.
		(x − 2)				+ y		> 4.

Область определения D(z) открытая (рисунок 1).

1.2.2 Для функции z = 4 1 − x2 − y2 найти:

а) область определения и изобразить ее геометрически;

б) lim 4 1 − x2 − y2 ;

x→ 0 y → 0

в) установить непрерывность ее в точке О(0; 0).

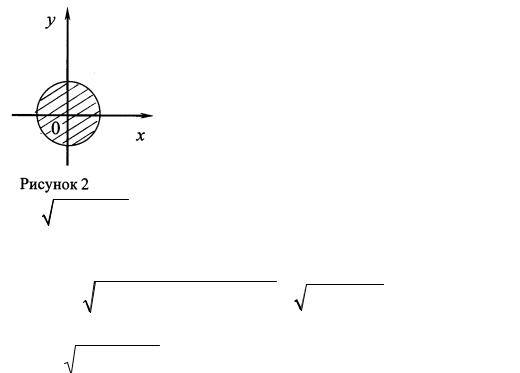
		5
Решение:
а) D(z) = {(x, y) R /1 − x2		− y2 ≥ 0}.
	2
1 − x2 − y2 ≥ 0,	x2 + y2 ≤ 1.

Все точки М(x, y), координаты которых удовлетворяют указанному неравенству, лежат внутри круга радиуса 1 и на границе этого круга. Эта область определения называется закрытой (замкнутой) областью определения для функции Z (рисунок 2);

б) lim 4 1 − x4 − y4						= 1;
x→ 0
y → 0
(M(x, y) → O(0;0);						x,	y → 0;
Δρ =	JJJJG	=	x2 +			y2 → 0);
Δρ =	MO	=	x2 +			y2 → 0);
в) очевидно, для функции z имеем
lim z = lim				(	4 1− (x +		x)2 − ( y + y)2 − 4 1− x2 − y2 = 0	)	,
x→0			x→0	(				)
y→0			y→0
значит, функция z = 4 1 − x2 − y2							непрерывна в точке О(0; 0).

Заметим, что в примере 1.2.1 линия AOMN сплошь состоит из точек разрыва.

1.2.3 Рассмотрим функцию	z =		2xy	. Исследуем ее на непрерыв-
		x	+ y2

ность.

Решение

Очевидно, что эта функция определена в каждой точке (x, y) R2 , кроме точки О(0; 0). Для этой функции точка О(0; 0) – точка разрыва.

Очевидно, lim	2xy	не существует (в зависимости от пути, на-
Очевидно, lim	x2 + y2	не существует (в зависимости от пути, на-
x→ 0	x2 + y2
y → 0

пример, который определяется прямой y = kx , ведущий от переменной точки М(x, y) к точке О(0; 0), получаем, что

lim	2ky	= lim	2xkx	=		2k
lim	x2 + y2	= lim	x2 + k 2 x2	=	1	+ k 2
x→0	x2 + y2	x→0	x2 + k 2 x2		1	+ k 2
y→0

не есть постоянная величина, а зависит от k).

1.2.4 Рассмотрим примеры нахождения частных и полного приращения функции z = f (x, y) на конкретных примерах. По определению, част-

ное приращение функции z = f (x, y) по переменной х (обозначается символом x z ), по переменной y (обозначается символом y z ), полное приращение z определяется символом z , находятся следующим образом:

x z = f (x + x, y) − f (x, y) ; y z = f (x, y + y) − f (x, y) ;

z = f (x + x, y + y) − f (x, y).

Так, для функции z = 2x + 3y имеем

z = 2(x + x) + 3(y + y) − (2x + 3y) = 2 x + 3 y;

x z = 2(x + x) + 3y − (2x + 3y) = 2 x; y z = 2x + 3(y + y) − (2x + 3y) = 3 y.

Заметим, для линейной функции ( z = 2x + 3y ) имеем z = x z + y z.

1.2.5 z = xy . Найти частные и полное приращения функции.

Решение

x z = (x + x)y − xy = x y; x z = x(y + y) − xy = x y;

z = (x + x)(y + y) − xy = x y + x y + x y.

Для нелинейной функции (здесь z = xy) z ≠ x z + y z.

1.3 Примеры и задачи для самостоятельной работы

Для функции z = f (x, y), см. примеры 1.3.1–1.3.10, найти:

а) область определения и изобразить ее геометрически; б) исследовать функцию на непрерывность.


1.3.1	z =	2			+				y		.
1.3.1	z =	x - y			+			x + y			.
				2		y	2
1.3.2	z = ln		x		−	y			−	1 .
1.3.2	z = ln				−				−	1 .
		9			4

1.3.3 z = arcsin(x2 + y2 − 3) .

1.3.4z =1+ − (x − y)2 .

1.3.5z = e x2+y2 -3 .

1.3.6z = x + y ln ( y2 - x2 ) .

1.3.7	z =	x2 − 16 + 16 − y2 .
1.3.8	z =	1	.
		1− x2 − y2

y 1.3.9 z = 3x + 2 − x + y .

1.3.10 z = ln x + ln cos y .

2 Частные производные функции нескольких переменных, дифференцируемость функции нескольких переменных. Дифференциал функции нескольких переменных

2.1 Основные понятия, теоретические вопросы

1 Частные и полное приращения ФНП.

2 Определение производной функции y = f(x).

3 Определения и обозначения частных производных ФНП.

4 Правила вычисления частных производных. Геометрический смысл частных производных.

5Механический смысл частных производных.

6Дифференцируемость ФНП (необходимые и достаточные условия). Достаточное условие дифференцируемости функции y = f(x).

7Полный дифференциал ФНП.

8Применение дифференциала ФНП в приближенных вычислениях.

Рекомендуемая литература: [1, С. 124, 125; 5, С. 251–261].

2.2 Образцы решения примеров и задач

2.2.1 Для функции z = ln(2 y −

а) частные производные ∂∂xz и

б) полный дифференциал dz.

x) −	1	найти:
	x2 − 4x + y2

∂∂yz ;

Решение:

∂z ∂x

а) находим частные производные:

(−1)+

2x − 4

x − 2

;

2y − x

( x2 − 4x + y2 )3

x − 2y

(x2

− 4x + y2 )

x2 − 4x + y2

∂z

∂y =

2y =

;

2y − x

( x2 − 4x + y2 )3

2 y − x

( x2 − 4x + y2 )3

б) полный дифференциал dz функции z = f (x, y) находим по формуле

dz = ∂z dx +

∂z

dy .

∂x

∂y

dz = ∂z dx +

∂z

x − 2

dy =

dx +

− 2y

(x2

− 4x + y2 )

∂x

∂y

x2 − 4x + y2

dy.

(x2

− 4x + y2 )

x2 −

2y − x

4x + y2

2.3 Примеры и задачи для самостоятельной работы

Для функции z = f (x, y), см. примеры 2.3.1–2.3.10, найти:

а) частные производные ∂∂xz и ∂∂yz ;

б) полный дифференциал dz.

2.3.1z = x3 + y3 − 3xy.

2.3.2z = x2 y3 .

x2 − y2

2.3.3z = x2 + y2 .

2.3.4z = sin2 x + cos2 y.

2.3.5z = yxy .

				x
2.3.6	z = ln 1+			x	.
2.3.6	z = ln 1+				.
				y
2.3.7	z = ln tg	x	.
2.3.7	z = ln tg		.
		y

2.3.8z = arctg x2xy− 1 .

2.3.9z =1+ − (x − y)2 .

2.3.10z = x + y ln ( y2 − x) .

2.3.11Вычислить приближенно (с точностью до 10-2) с помощью

дифференциала функции значения:

а) sin 32° cos59°;

б) (1,02)3 (0,97)2 .

3 Дифференцирование сложных функций нескольких переменных, дифференцирование неявных функций

3.1 Основные понятия, теоретические вопросы

1 Сложная функция одной, двух и большего числа переменных. 2 Неявная функция одной и большего числа переменных.

3Производная сложной ФНП.

4Полная производная сложной функции.

5Производная от функции, заданной неявно.

6Инвариантность полного дифференциала ФНП.

Рекомендуемая литература: [1, С. 129–131; 5, С. 262–268].

3.2 Образцы решения примеров и задач

3.2.1

Продифференцировать

сложную

функцию z =

x = u sin v,

y = u cosv .

Решение

Если

z = f (x, y), где x = x(u,v),

то частные производные

y = y(u,v),

определяют по формулам:

∂z

∂x

∂z

∂y

;

∂u

∂x

∂u

∂y

∂u

∂z

∂x

∂z

∂y .

∂v

∂x

∂v

∂y

∂v

arctg xy ,

∂∂uz и ∂∂vz

(3.1)

Для функции (см. п. 3.2.1) имеем:

∂z

;

∂x

x2 + y2

∂z

−

= −

;

∂y

+ x

∂x

= sin v;

∂x

= u cosv;

∂y

= cosv;

∂y = −u sin v.

∂u

∂v

∂u

∂v

Учитывая формулы (3.1), получим

∂z

sin v -

cosv =

∂u

x2 + y2

y2 + x2

u cosv sin v

−

= 0.

(u cosv)2 + (sin v)2

u cosv +

u sin v = (u cosv)2 + (u sin v)2

= 1.

2 + x2

y2 + x2

(u cosv)2 + (u sin v)2

3.2.2

Найти

полную

производную функции z = e3x+2 y , где

x = cost, y = t2 .

Решение

Здесь z = z(t) , дифференцируем ее и получаем «полную» производ-

ную функции z по аргументу t, а именно

dzdt = ∂∂xz dxdt + ∂∂yz dydt = e3x+2y 3 (− sin t ) + e3x+2y 2 2t =

=e3x+2y (4t − 3sin t ) = e3cos t+2t2 (4t − 3sin t ).

3.2.3Продифференцировать функцию z = f (x, y), заданную неявно уравнением

xz3 - yz + x2 y - 3x + 4 = 0.

(3.2)

Решение

Если уравнение F(x, y, z) = 0 определяет функцию двух переменных

1 / 31 2 3 > Следующая >>>

Соседние файлы в папке универ

#
29.02.20161.23 Mб25История Беларуси.Экономическое и культурное развитие.pdf
#
29.02.2016395.55 Кб20Культура Беларуси в 20-30 гг. ХХ в.Метод. рек.pdf
#
29.02.2016364.58 Кб20Мат.анализ.Метод.указ. к практ.зан.pdf
#
29.02.2016434.53 Кб147Матем. статистика. Метод. укза. к практич.pdf
#
29.02.20161.91 Mб28Начерт.геом.и инж.графика.Индивид.задания.pdf
#
29.02.2016393.07 Кб32Функция нескольких переменных.Метод. указ. к практ. занятиям.pdf