
универ / Высш. матем. Теория вероятностей Ч
.1.pdf21
урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.
9 По объекту производится три одиночных независимых выстрела. Вероятность попадания при первом выстреле равна 0,4; при втором – 0,5; при третьем – 0,7. Для вывода объекта из строя заведомо достаточно трех попаданий, при двух попаданиях он выходит из строя с вероятностью 0,6; при одном – с вероятностью 0,2. Найти вероятность того, что в результате трех выстрелов объект будет выведен из строя.
10 Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6; 0,5 и 0,4.
Домашнее задание
1 Повторение испытаний. Формулы Бернулли и Пуассона. Локальная и интегральная теоремы Лапласа.
2 Решить задачи.
Задача 1. Имеются две урны. В первой урне два белых и три черных шара, во второй – три белых и пять черных. Из первой и второй урн, не глядя, берут по одному шару и кладут их в третью урну. Шары в третьей урне перемешивают и берут из нее наугад один шар. Найти вероятность того, что этот шар белый.
Задача 2. Один из трех стрелков вызывается на линию огня и производит выстрел. Цель поражена. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго – 0,5, для третьего – 0,8. Найти вероятность того, что выстрел произведен вторым стрелком.
Задача 3. С первого автомата на сборку поступает 40 %, со второго – 35 %, с третьего – 25 % деталей. Среди деталей первого автомата 0,2 % бракованных, второго – 0,3 %, третьего – 0,5 %. Найти вероятность того, что:
а) поступившая на сборку деталь бракованная; б) деталь, оказавшаяся бракованной, изготовлена на втором автомате.
Задача 4. В группе из 20 стрелков пять отличных, девять хороших и шесть посредственных. При одном выстреле отличный стрелок попадает в мишень с вероятностью 0,9, хороший – с вероятностью 0,8 и посредственный – с вероятностью 0,7. Наугад выбранный стрелок выстрелил дважды; отмечено одно попадание и один промах. Каким, вероятнее всего, был этот стрелок: отличным, хорошим или посредственным?

22
5 Повторение испытаний. Формулы Бернулли, Пуассона. Локальная и интегральная теоремы Лапласа
Пусть производится n испытаний, причем выполняются следующие условия:
–испытания независимы, т. е. начальные условия перед каждым испытанием абсолютно одинаковы;
–в каждом испытании интересующее нас событие А может произойти с вероятностью p.
Тогда вероятность того, что в n испытаниях событие А наступит ровно k раз (безразлично в какой последовательности), вычисляется по фор-
муле Бернулли:
P |
(k )=Ck pk qn−k , |
(5.1) |
n |
n |
|
где q =1 − p .
В случае, если n велико, то есть npq 1 (значительно больше едини-
цы), то данную вероятность можно найти по асимптотической формуле
(локальная теорема Лапласа):
|
|
|
P |
(k )= |
1 |
ϕ(x), |
|
|
(5.2) |
||
|
|
|
|
|
|
||||||
|
|
|
n |
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
x = |
k − np |
, ϕ(x) определяется формулой ϕ(x)= |
1 |
e− |
x2 |
|||||
2 |
. |
||||||||||
npq |
2π |
||||||||||
|
|
|
|
|
|
|
|
|
|||
Существует таблица значений функции ϕ(x) для 0 ≤ x ≤ 4. Для отрицательных значений переменной надо помнить, что ϕ(−x)=ϕ(x).
В тех случаях, когда число испытаний n велико, а вероятность p ма-
ла, пользуются формулой Пуассона:
P (k )= λk e−λ , |
(5.3) |
n |
k! |
|
где λ – среднее число появлений события в различных сериях испытаний, λ = n p .
Вероятность того, что в n независимых испытаниях (n велико, а p существенно отличается от 0 и 1) событие наступит не менее k1 раз и не
более k2 раз, приближенно равна:
P |
(k ;k |
)=Φ(x′′)− Φ(x′), |
(5.4) |
n |
1 2 |
|
|
где

23
x |
′ |
= |
k1 − np |
|
; |
|
|
|
|
|
||
|
npq |
|
|
|
|
|
||||||
x |
′′ |
= |
k2 − np |
, |
|
|
|
|
|
|||
npq |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
x |
z2 |
|
||
функция Φ(x) определяется формулой Φ(x)= |
∫e− |
|
dz |
и называется |
||||||||
2 |
||||||||||||
2π |
||||||||||||
функцией Лапласа. |
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 ≤ x ≤5 , для |
||
Существует таблица значений функции Лапласа для |
||||||||||||
значений х < 0 следует помнить, что Φ(−x)= −Φ(x). |
|
|
|
|
||||||||
Точность асимптотических формул (локальной, интегральной Лапласа, Пуассона) тем выше, чем больше n.
Образцы решения задач
Пример 1 – Бросаются 3 игральные кости. Какова вероятность того, что выпадет одна шестерка?
Решение
Из условия задачи n =3 , k =1. Рассматривается событие А – выпаде-
ние шестерки при одном броске кости. Тогда p = 16 , q =1 − p = 56 .
По формуле (5.1) имеем
|
P |
(1)=C1 |
|
|
1 1 |
|
|
5 3−1 |
= |
3! |
1 25 = 25 . |
||
|
|
|
|
|
|
|
|
||||||
|
3 |
3 |
|
6 |
|
6 |
|
2! 1! 6 36 72 |
|||||
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
25 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2 – В лаборатории проводится серия из 400 опытов по обнаружению микроба в растворе. Вероятность появления микроба в каждом отдельном опыте равна 0,2. Найти вероятность того, что микроб будет обнаружен в 80 опытах.
Решение
Число испытаний n = 400 велико, а вероятность наступления события в одном испытании отличается от 0 и 1, поэтому для определения вероятности воспользуемся локальной теоремой Лапласа. n = 400, k =80 ,
p = 0,2 , q = 0,8 , x = |
80 − 400 0,2 |
= 0 . Для x =0 определяем значение |
|
400 0,2 0,8 |
|||
|
|

24
ϕ(0)= 0,3989 .
По формуле (5.2) находим
P400 |
(80)= |
|
1 |
0,3989 |
= 0,0498 . |
|
0,2 0,8 |
||||
|
400 |
|
|
||
Ответ: 0,04989.
Пример 3 – Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
Решение
По условию n =5000 , p = 0,0002 , k =3. Речь в задаче идет о практи-
чески невозможном событии. В этом случае используем формулу Пуассона
(5.3). Находим λ = n p =5000 0,0002 =1,
P5000 (3)=13 3!e−1 = 61e ≈ 0,06 .
Ответ: 0,06.
Пример 4 – Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется не прошедших проверку от 70 до 100 деталей.
Решение
Требуется найти вероятность P400 (70;100). В данном случае необходимо воспользоваться интегральной теоремой Лапласа и формулой (5.4).
x |
′ |
|
|
k1 − np |
|
|
|
70 −500 0,2 |
|
|
||||
|
= |
|
|
|
= |
|
|
|
= −1,25 |
; |
||||
|
|
npq |
|
|
400 0,2 0,8 |
|||||||||
x |
′′ |
= |
k2 − np |
|
= |
100 − 400 0,2 |
= 2,5. |
|
||||||
|
400 0,2 0,8 |
|
||||||||||||
|
npq |
|
|
|
||||||||||
По таблице значений функции Φ(x) находим Φ(2,5)= 0,4938 и Φ(1,25)= 0,3944 . Искомая вероятность равна:
P400 (70;100)=Φ(2,5)−Φ(−1, 25)= Φ(2,5)+Φ(1, 25)= = 0, 4938 +0,3944 = 0,8882.
Ответ: 0,8882.
25
Задачи для самостоятельного решения
1 Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех; б) выиграть не менее двух партий из четырех или не менее трех пар-
тий из пяти?
Ничьи во внимание не принимаются.
2 В семье 5 детей. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди этих детей:
а) два мальчика; б) не более двух мальчиков;
в) более двух мальчиков; г) не менее двух и не более трех мальчиков.
3 Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, что событие А появится хотя бы 2 раза.
4 Монета подбрасывается 10 раз. Определить погрешность локальной теоремы Лапласа при определении вероятностей следующих событий: «герб» выпадет 2 раза; «герб» выпадет 5 раз.
5 Вероятность поражения мишени стрелком при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена:
а) ровно 75 раз; б) не менее 75 и не более 90 раз; в) не более 74 раз; г) не менее 75 раз.
6 Прядильщица обслуживает 100 веретен. Вероятность обрыва нити в одном веретене в течение 1 мин 0,004. Найти вероятность того, что в течение 1 мин обрыв произойдет на пяти веретенах.
7 Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение 1 мин абонент позвонит на коммутатор, равна 0,02. Какое из двух событий вероятнее: в течение 1 мин позвонят 3 абонента или позвонят 4 абонента?
8 В книге, состоящей из 500 страниц, обнаружено 15 опечаток. Какова вероятность обнаружить на странице, открытой наудачу, 2 опечатки, если на каждой странице в среднем 1400 знаков?
26
Домашнее задание
1 Дискретные случайные величины, их законы распределения. Распределения биномиальное и пуассоновское. Числовые характеристики дискретных случайных величин.
2 Решить задачи.
Задача 1. Стрелок стреляет по цели до первого попадания. Найти вероятность того, что у стрелка останется хотя бы один неизрасходованный патрон, если он получил десять патронов, и вероятность попадания в цель при каждом выстреле постоянна и равна 0,2.
Задача 2. Вероятность того, что данный баскетболист забросит мяч в корзину, равна 0,3. Произведено 12 бросков. Найти наивероятнейшее число попаданий и соответствующую вероятность.
Задача 3. Что вероятнее – победить равносильного противника в игре, в которой нет ничейных исходов, выиграв не менее четырех партий из пяти или не менее пяти партий из восьми?
Задача 4. Завод выпускает в среднем 99,8 % доброкачественных и 0,2 % бракованных изделий. Какова вероятность того, что среди выбранных наугад 500 изделий бракованных будет больше трех?
Задача 5. В радиоаппаратуре за год работы происходит замена 10 деталей. Подсчитать вероятность отказа аппаратуры за 1000 ч непрерывной работы из-за выхода из строя деталей.
Задача 6. Из кошелька на стол высыпали 25 монет. Какова вероятность того, что число монет, упавших гербом вверх, заключено между 8 и 15, включая и эти два крайних значения?
6 Дискретные случайные величины, их законы распределения и числовые характеристики. Биномиальное и пуассоновское распределения
Случайной величиной называется числовая функция, определенная на пространстве элементарных событий Ω, которая каждому элементарному событию ω ставит в соответствие некоторое число.
При этом предполагается, что определена вероятность события X < x для любых значений x.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
27
Непрерывной называют случайную величину, которая может принимать все значения из некоторого промежутка.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной
величины первая строка таблицы содержит возможные значения xk , а вто- |
|||||||||
рая – их вероятности pk |
= P(X = xk ), причем ∑pk =1. |
||||||||
|
|
|
|
|
|
|
k |
||
|
|
|
|
|
|
|
|
|
|
|
xk |
|
x1 |
x2 |
x3 |
… |
|
xn |
|
|
pk |
|
p1 |
p2 |
p3 |
… |
|
pn |
|
Существует универсальный способ задания закона распределения, который годится для случайных величин любого типа: функцией распределения случайной величины Х называется функция F(x), равная вероятности того, что Х примет значение меньше, чем число х, т. е. F(x)=P(X <x).
Из определения следует, что 0 ≤ F (x)≤1 и P(a < X <b)=F(b)−F(a).
Одна из числовых характеристик, фиксирующая положение случайной величины на числовой оси, то есть некоторое среднее взвешенное значение случайной величины, около которого группируются ее возможные значения, – математическое ожидание М(Х).
Для дискретной случайной величины математическое ожидание вычисляется по формуле
n |
|
M (X )= ∑xi pi . |
(6.1) |
i=1
Дисперсия D(X) – характеристика рассеяния, разбросанности случайной величины около ее математического ожидания.
Для дискретной случайной величины дисперсия вычисляется следующим образом:
n |
|
D(X )= ∑(xi − M (X ))2 pi . |
(6.2) |
i=1
Иногда дисперсию удобно вычислять по формуле
D(X )= M (X 2 )−(M (X ))2 |
n |
= ∑xi2 pi −(M (X ))2 . (6.3) |
|
|
i=1 |
Дисперсия имеет размерность квадрата отклонения случайной величины, что не всегда удобно. Наряду с дисперсией вводится еще одна ха-
рактеристика рассеяния – среднее квадратическое отклонение, которое

28 |
|
вычисляется по формуле |
|
σ (X )= D(X ). |
(6.4) |
Биномиальным называют закон распределения дискретной случайной величины Х – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p. Возможные значения случайной величины 0, 1, …, n, а соответствующие вероятности вычисляются по формуле Бернулли
p |
k |
= P(X = x |
)=Ck pk qn−k . |
(6.5) |
|
k |
n |
|
Для биномиального распределения M (X )= n p , D(X )= n p q .
Предельным случаем для биномиального распределения, если n неограниченно увеличивается и одновременно вероятность p неограниченно уменьшается, является распределение Пуассона. Возможные значения случайной величины 0, 1, …, k, …, а соответствующие вероятности вычисляются по формуле
p |
k |
= P(X = k )= |
e−λ λk |
, |
(6.6) |
|
k! |
||||||
|
|
|
|
|||
|
|
|
|
|
где λ = np .
Для этого распределения M (X )= λ , D(X )= λ .
Образцы решения задач
Пример 1 – В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 р. и десять выигрышей по 10 р. Написать закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение
Данная случайная величина Х: х1 = 50; х2 = 10; х3 = 0. Вероятности этих
возможныхзначений p = |
1 |
=0,01; |
p = |
|
10 |
=0,1; |
p = |
100 −10 −1 =0,89. |
||||
|
100 |
|||||||||||
1 |
100 |
|
2 |
|
3 |
100 |
||||||
|
Закон ее распределения имеет следующий вид (таблица 6.1). |
|||||||||||
|
Таблица 6.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
50 |
|
|
|
|
10 |
|
|
0 |
|
|
р |
|
0,01 |
|
|
|
|
0,1 |
|
|
0,89 |
|
29
Составим функцию распределения F(x):
x ≤0 :
F (x)= P(X < x)= 0 ;
0 < x ≤10 : F (x)= P(X < x)= P(X = 0)= 0,89 ;
10 < x ≤50 :
F (x)= P(X < x)= P(X = 0)+ P(X =10)= 0,89 + 0,1 = 0,99 ;
x >50 :
F (x)= P (X < x)= P (X = 0)+ P (X =10)+ P (X = 50)= = 0,89 +0,1 +0,01 =1;
0, x ≤ 0;
0,89, 0 < x ≤10;
F (x)=
0,99, 10 < x ≤50;1, x >50.
Ее график имеет вид (рисунок 6.1).
Рисунок 6.1
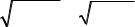
30
Числовые характеристики этой случайной величины:
3
M (X )= ∑xi pi =50 0,01 +10 0,1 + 0 0,89 =1,5 ;
i=1
3
D(X )= ∑xi2 pi −(M (X ))2 =502 0,01 +102 0,1 + 02 0,89 −(1,5)2 =
i=1
= 25 +10 − 2,25 =32,75 ;
σ (X )= D(X ) = 32,75 ≈5,72 .
Задачи для самостоятельного решения
1 В урне 5 белых и 25 черных шаров. Вынули наугад один шар. Случайная величина Х – число вынутых белых шаров. Требуется:
а) построить ряд распределения СВ Х; б) построить функцию распределения СВ Х; в) найти М(Х) и D(X).
2 В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины Х – числа стандартных деталей среди отобранных. Найти
М(Х), D(X).
3 Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа приборов таковы: р1 = 0,3; р2 = 0,4; р3 = 0,5; р4 = 0,6. Найти М(Х), D(X) и среднее квадратическое отклонение СВ Х – числа отказавших приборов.
4 Случайная величина Х может принимать два возможных значения: х1 с вероятностью 0,3 и х2 с вероятностью 0,7, причем х2 > х1. Найти х1 и х2,
зная, что М(Х) = 2,7 и D(X) = 0,21.
5 Дан перечень возможных значений дискретной случайной величи-
ны Х: х1 = 1; х2 = 2; х3 = 3, а также известно, что М(Х) = 2,3, М(Х 2) = 5,9.
Найти вероятности, соответствующие возможным значениям Х.
6 Даны независимые случайные величины Х и Y (таблицы 6.2 и 6.3).
Таблица 6.2
Х |
-1 |
0 |
1 |
р |
0,2 |
0,5 |
0,3 |
Таблица 6.3
Y |
2 |
4 |
p |
0,3 |
0,7 |
Найти математическое ожидание и дисперсию следующих случай-
ных величин: Х + Y; 2X – 3Y; X – Y + 5.
