Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусско-Российский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

универ / Высшая математикака.Метод. указ. и инд. задания

.pdf

Скачиваний:

Добавлен:

29.02.2016

Размер:

446.4 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Вариант 23

1 Функция w = z z−i отображает прямую y = x +1 на плоскость w .

Найти соответствующий образ.

2 Проверить выполнимость условий Коши-Римана для функции w = z2 −2iz на комплексной плоскости и найти её производную.

3	Найти и построить образ параболы y = x2			при отображении w =				1 .
								z
4	Найти линейное отображение с неподвижной точкой z1 =1−i , пе-
реводящее точку z2 = 2 −i в точку w =i .
5	Вычислить ∫	1	dz , где C – окружность			z −(1+i)	=1.

		z −(1+i)
	C			1
6	Разложить	в ряд	Лорана функцию				в кольце
					(z −2)(z −3)

3 < z < ∞.

7 С помощью вычетов вычислить интеграл z∫=2 (z −i)(z −3)dz .

Список литературы

1 Пантелеев, А. В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах : учеб. пособие для вузов / А. В. Пантелеев, А. С. Якимова. – 2-е изд., стер. – М. : Высш. шк., 2007. – 445 с.

2 Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа : учеб. пособие для втузов. – 2-е изд. / В. А. Болтов [и др.] ; под ред. А. В. Ефимова и Б. П. Демидовича. – М. : Наука, Главная редакция физ.-мат. литературы, 1986. – 368 с.

3 Сборник задач по курсу высшей математики / Под ред. Г. И. Круч-

ковича. – М. : Высш. шк., 1973. – 576 с.

4 Письменный, Д. Т. Конспект лекций по высшей математике / Д. Т. Письменный. – М. : Айрис-пресс, 2005. – Ч. 2. – 256 с.

5 Функции комплексного переменного. Задачи и упражнения / М. Л. Краснов [и др.]. – М. : Наука, 1981.

ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»

Кафедра «Высшая математика»

ВЫСШАЯ МАТЕМАТИКА

Методические указания и варианты индивидуальных заданий по теме

«Основныепонятиятеориифункцийкомплекснойпеременной» для студентов дневной и заочной форм обучения электротехнических специальностей

Могилев 2009

УДК 51

ББК 22.1 В 93

Рекомендовано к опубликованию учебно-методическим управлением

ГУ ВПО «Белорусско-Российский университет»

Одобрено кафедрой «Высшая математика» «28» января 2009 г., протокол № 5

Составители: В. Г. Замураев; В. И. Мармазеев; Т. Ю. Орлова

Рецензент канд. физ.-мат. наук, доц. Л. В. Плетнёв

Методические указания предназначены для самостоятельной подготовки студентов дневной и заочной форм обучения электротехнических специальностей.

		Учебное издание
	ВЫСШАЯ МАТЕМАТИКА
Ответственный за выпуск			Л. В. Плетнёв
Технический редактор			А. Т. Червинская
Компьютерная верстка			Н. П. Полевничая
Подписано в печать	. Формат 60×84/16. Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл.-печ. л.		. Уч.-изд. л.	. Тираж 99 экз. Заказ №	.

Издатель и полиграфическое исполнение Государственное учреждение высшего профессионального образования

«Белорусско-Российский университет» ЛИ № 02330/375 от 29.06.2004 г. 212000, г. Могилев, пр. Мира, 43

Найти дробно-линейную функцию, отображающую полуплоскость

Im z > 0

на круг

<1 так, чтобы точки

z1 = −1, z2 = 0 , z3 =1 границы

Im z = 0

перешли соответственно в точки

w1 =1,

w2 =i ,

w3 = −1 границы

=1.

5 Вычислить ∫zdz , где C – замкнутый контур x = cost,

0 ≤t ≤ 2π .

y =sin t,

Разложить в ряд Лорана функцию

ez −1

по степеням

z и найти

область сходимости ряда.

С помощью вычетов вычислить интеграл

∫

dz , где C – ок-

z −a

ружность

= R , R >

Вариант 22

Функция w =

отображает прямую y = x на плоскость w . Най-

z −i

ти соответствующий образ.

2 Проверить выполнимость условий Коши-Римана для функции w = 1z в области D ={z C z ≠ 0} и найти производную этой функции.

3На какую область в плоскости ( w ) отображает функция w =iz +1 треугольник, ограниченный линиями: x = 0 , y = 0 , x + y =1?

4Найти дробно-линейную функцию, отображающую полуплоскость Im z > 0 на полуплоскость Im w > 0 так, чтобы точки z1 =1, z2 = 2 , z3 =3

границы Im z = 0 перешли соответственно в точки w1 = 0 , w2 =1, w3 = ∞ границы Im w = 0 .

5	Вычислить ∫	1	dz , где C – эллипс x =3cost,		0 ≤t ≤ 2π .
5	Вычислить ∫		dz , где C – эллипс x =3cost,		0 ≤t ≤ 2π .
	C	z −4		y = 2sin t,
6	Разложить в ряд Лорана функцию			1	в кольце 2 <	z	<3 .
				1
				(z −2)(z −3)
				(z −2)(z −3)

7 С помощью вычетов вычислить интеграл C∫(z −a)(z −b)dz , где

C – окружность z = R , R > a , R > b , a ≠ b .

©ГУ ВПО «Белорусско-Российский университет», 2009

			z		dz
5 Объясните, почему можно утверждать, что ∫0					dz		не зависит от
5 Объясните, почему можно утверждать, что ∫0					z2 −9		не зависит от
пути интегрирования в верхней полуплоскости	Im z > 0 , но этого нельзя
утверждать для левой полуплоскости Re z < 0 .
6 Разложить в ряд Лорана функцию 1 −cos z			по степеням z и найти
z2
область сходимости ряда.						z2
7 С помощью вычетов вычислить интеграл	∫					z2		dz .
7 С помощью вычетов вычислить интеграл	∫		(z	2		+1)(z −2)		dz .
	z	=3	(z			+1)(z −2)

Вариант 20

1 Функция w = z2 отображает линию y =b , где b = const , на плос-

кость w . Найти соответствующий образ.

2 Указать точки плоскости, в которых нарушена конформность ото-

бражения w = 17 z7 +64z .

3 Показать, что угол между прямыми y = x и y = 0 не изменится при отображении w = zi +1+i .

4 На какую область в плоскости w

отобразит функция

w =1− z i

верхний полукруг

<1; Im z > 0 ?

1 + z

5 Вычислить ∫

, где путь интегрирования C – это: а) окруж-

C z −1 +

ность

= 2 ; б) окружность

z −1

= 6 .

1 sin2 2

по степеням

z и найти

6 Разложить в ряд Лорана функцию

область сходимости ряда.

7 С помощью вычетов вычислить интеграл

∫

Вариант 21

=5 z (z + 2)(z +

1 Функция w = z2

отображает линию

y = kx , где k = const , на плос-

кость w . Найти соответствующий образ.

2 Указать точки плоскости, в которых нарушена конформность отображения w = 13 z3 −(1 +i)z2 − z + 2i .

3 На какую область в плоскости w отображает функция w = 2z −1 треугольник с вершинами в точках (0;0), (1;0), (0;1)?

Содержание

1 Элементы теории аналитических функций ………………….…...4

1.1Функции комплексного переменного …………………………..4

1.2Аналитические функции ………………………………………...5

1.3Конформные отображения …………………………………..….7

1.4Интегрирование …………………………………………………12

1.5Степенные ряды …………………………………………………14

1.6Вычеты и их применение …………………………………….....15 2 Теоретические вопросы и задачи ………………………………...18

2.1Теоретические вопросы …………………………………………18

2.2Теоретические задачи …………………………………………...18 3 Варианты заданий …………………………………………………19

Список литературы ……………………………………………...…..32

1 Элементы теории аналитических функций

1.1 Функции комплексного переменного

Множество точек D комплексной плоскости называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат данному множеству. Связное открытое множество точек комплексной плоскости называется областью. Область D называется односвязной, если любая непрерывная замкнутая самонепересекающаяся кривая, проведенная в D , ограничивает некоторую область G , целиком принадлежащую D . В простых случаях можно задавать область в комплексной плоскости, накладывая некоторые ограничения на комплексную переменную.

Пример 1. Записать с помощью неравенств область, которая является внутренностью эллипса с фокусами в точках 1+i , 3 +i и большой полуосью, равной 3.

Решение

Заметим, что точка z является внутренней точкой эллипса тогда, и только тогда, когда сумма расстояний от неё до фокусов будет меньше большой оси. Следовательно, наша область может быть записана в виде

неравенства z −(1+i) + z −(3 +i) < 6 .

Говорят, что в области D определена функция w комплексного переменного z , если каждому значению комплексной переменной z = x +iy D по определённому правилу поставлено в соответствие значе-

ние	переменной	w =u +iv ,	и	символически	записывают
f (z)=w =u(x, y)+iv(x, y), где v(x, y)= Im f (z), u (x, y)= Re f (z). С гео-
метрической точки зрения функцию			f (z)	можно рассматривать как ото-

бражение области D плоскости (z) на некоторое множество G плоскости (w). При этом говорят, что w – образ точки z , а точка z – прообраз точки w при отображении, осуществляемом функцией w = f (z).

Пример 2. При отображении, осуществляемом функцией		w = z2 ,
найти образы прямых x = 2, y =1.
Решение			w :
Выделим действительную и мнимую	части функции
w =(x +iy)2 = x2 − y2 +i 2 y , т. е. u = x2 − y2 , v = 2xy . Когда точка z		пробе-
гает в плоскости (z) прямую x = 2, то её образ w в плоскости (w)		пробе-
гает линию u = 4 − y2 , v = 4 y ( −∞ < y < +∞) или,	исключая параметр		y ,

∞

Определить область сходимости ряда ∑

n=1 (z + 2i)

С помощью вычетов вычислить интеграл

∫

(z −1)

sin

dz .

z −1

Вариант 18

z−1

Функция

w = 1 отображает линию

y = x −1 плоскости z

на плос-

кость w . Найти соответствующий образ.

w = f (z)

по её действи-

Восстановить аналитическую функцию

тельной части Re f (z)= x2 − y2 + xy .

На какую область в плоскости ( w ) отображает функция w = 2z +3

прямоугольник плоскости z с вершинами в точках A(0;0),

B(−1;0),

C (−1;1), D(0;1)?

Найти дробно-линейную функцию, отображающую полуплоскость

Re z > 0 в круг

<1 так, чтобы точки

z1 = −i ,

z2 = 0 ,

z3 =i

границы

Re z = 0 перешли соответственно в точки

w1 = −1,

w2 =i ,

w3 =1 границы

=1.

Объясните, почему можно утверждать, что C∫

равен нулю, ко-

z2 +3

гда C – окружность

=1, но это неверно, когда C – окружность

=3.

Разложить в ряд Лорана функцию z2ez по степеням z

и найти об-

ласть сходимости ряда.

С помощью вычетов вычислить интеграл

∫

dz .

(z −1)(z −2)2

z−2

=1 2

Вариант 19

1Функция w = z2 отображает линию x = a , где a = const , на плоскость w . Найти соответствующий образ.

2Указать точки плоскости, в которых нарушена конформность ото-

бражения w = z5 +5z .

3На какую область в плоскости ( w ) отображает функция w = 2z −1 прямоугольник с вершинами в точках (0;0), (1;0), (1;1), (0;1)?

4Найти дробно-линейную функцию, отображающую круг z <1 в

круг	w −i	<3 так, чтобы точки z1 = −1, z2 =i , z3 =1 границы	z	=1 пере-

шли	соответственно в точки w1 = −3 +i , w2 = 4i , w3 =3 +i границы

w −i =3 .

Вариант 16

1 Функция w = 1z отображает окружность x2 + y2 = R2 на плоскость w . Найти соответствующий образ.

2Восстановить аналитическую функцию w = f (z) по её действительной части Re f (z)=3x2 y − y3 .

3В какие линии плоскости w преобразуются оси координат плоскости z функцией w =iz −2 ?

4Найти дробно-линейную функцию по следующим условиям: точки

12 и 2 неподвижны, а точка 54 + 34 i переходит в ∞.

5 Вычислить ∫z2dz , где путь интегрирования C – это: а) прямоли-

нейный отрезок, соединяющий точку z1 = 0 с точкой z2 =1+i ; б) ломанная, соединяющая точки z1 = 0 , z2 =1+i , z3 =1.

6 Разложить в ряд Лорана функцию sin	1	по степеням z −2 и най-
6 Разложить в ряд Лорана функцию sin	z −2	по степеням z −2 и най-
ти область сходимости ряда.	z −2
ти область сходимости ряда.			z
7 С помощью вычетов вычислить интеграл ∫			z	dz , где C	– прямо-
7 С помощью вычетов вычислить интеграл ∫				dz , где C	– прямо-
	C cos z
угольник с вершинами в точках z1 = −i , z2 = 2 −i ,		z3 = 2 +i , z4 =i .
Вариант 17
1 Функция w = 1 отображает прямую	y = 4 плоскости z				на плос-
z
кость w . Найти соответствующий образ.
2 Восстановить аналитическую функцию w = f (z) по её мнимой час-
ти Im f (z)= x3 +6x2 y −3xy2 −2 y2 .
3 Показать, что угол между прямыми	y =1 и y = x −1 не изменится
при отображении w =(1 +i)z +1 −i .

4 Найти дробно-линейную функцию, отображающую полуплоскость

Im z <3 на полуплоскость Im w > −1 так, чтобы точки		z1 =3i , z2 =3i −2 ,
z3 =3i +1	границы Im z =3перешли соответственно	в точки w1 = −i ,
w2 = −i +1,	w3 = −i +6 границы Im w = −1.

5 Вычислить ∫zdz , где путь интегрирования C – это: а) прямолиней-

ный отрезок, соединяющий точку z1 = 0 с точкой z2 =1+i ; б) дуга параболы y = x2 , соединяющая точки z1 = 0 , z2 =1+i .

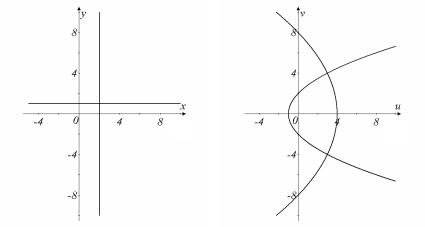
u = 4 − v2	. Это уравнение определяет в плоскости	(w) параболу. Анало-
16

гично прямая y =1 перейдёт при нашем отображении в параболу u = v2 −1 4

(рисунок 1).

y						v

x	u

Рисунок 1

1.2 Аналитические функции

Если w = f (z) – однозначная функция, заданная в области D , то её производной в точке z D называется предел

lim	w	= lim	f (z + z)− f (z)	= f ′(z)= dw		,
	z		z
z→0		z→0			dz
когда z любым образом стремится к нулю.
Однозначная в области			D функция w = f (z),		имеющая непрерыв-

ную производную в любой точке области, называется аналитической

функцией	на	этой	области.	Для	того,	чтобы	функция
f (z)=u (x, y)+iv(x, y)			была аналитической в области			D плоскости (z),

необходимо и достаточно, чтобы частные производные первого порядка функций u и v были непрерывны в D и выполнялись условия Коши-

Римана

∂u	=	∂v	;	∂u	= −	∂v .	(1)
∂x		∂y		∂y		∂x

Функции u и v называются сопряжёнными друг к другу на D . При вы-

полнении условий (1) производная				f ′(z) может быть записана в виде
	′	∂u	∂v ∂v	∂u ∂u ∂u ∂v			∂v
f	′	(z)= ∂x	+i ∂x = ∂y −i ∂y = ∂x −i ∂y = ∂y			+i ∂x .		(2)
f		(z)= ∂x	+i ∂x = ∂y −i ∂y = ∂x −i ∂y = ∂y			+i ∂x .		(2)
Пример 3. Найти область аналитичности функции							f (z)= e2 z	и вы-
числить f ′(z).
Решение
Имеем f (z)= e2 z = e2 x (cos 2 y +isin 2 y), т. е.
		u (x, y)= e2 x cos 2 y ,			v(x, y)= e2 x sin 2 y .
Следовательно,
∂u = 2e2 x cos 2 y ; ∂u			= −2e2 x sin 2 y ;		∂v = 2e2 x sin 2 y ;	∂v	= 2e2 x cos 2 y .
∂x		∂y			∂x	∂y

Значит, условия (1) выполняются во всей плоскости, и по формуле (2) имеем

f ′(z)=(e2 z )′ = 2e2 x cos 2 y +i 2e2 x sin 2 y = 2e2 x (cos 2 y +isin 2 y)= 2e2 z .

Действительная и мнимая части аналитической в области D функции f (z)=u (x, y)+iv(x, y) являются гармоническими в этой области функ-

циями, т. е. справедливы равенства:

u ≡	∂2u	+	∂2u	= 0 ; v ≡	∂2v	+	∂2v	= 0 .
	∂x2		∂y2		∂x2		∂y2

Аналитическая в области D функция определяется с точностью до постоянной заданием своей действительной или мнимой части. Например, если u (x, y) – действительная часть аналитической в области D функции

f (z), то

(x, y)
v(x, y)= Im f (z)= ∫	−u′ydx +u′xdy ,	(3)
(x0 , y0 )

где (x0 , y0 ) – фиксированная точка в области D , рассматриваемой как об-

ласть определения вещественной функции двух переменных, а путь интегрирования целиком лежит в области D .

3 В какие линии плоскости w преобразуются оси координат плоскости z функцией w =iz +1?

4 Найти дробно-линейную функцию, отображающую полуплоскость Im z > 0 на полуплоскость Im w > 0 так, чтобы точки z1 = ∞, z2 = 0 , z3 =1

границы Im z = 0 перешли соответственно в точки w1 = 0 , w2 =1,				w3 = ∞
границы Im w = 0 .
5 Вычислить ∫Im zdz , где путь интегрирования C – это: а) прямоли-
			C
нейный отрезок,			соединяющий точку z1 =3 с точкой z2 = −3; б)	полуок-
ружность	z	=3,	0 ≤ arg z ≤π .

6		∞	(		2 +i			2 )n
6	Определить область сходимости ряда ∑					z	n	.
		n=1				z
				∫				1
7	С помощью вычетов вычислить интеграл			∫		z ez dz .
Вариант 15				z	=1
				z	=1

1	Функция w = 1	отображает прямую y = x				плоскости z на плос-
	z

кость w . Найти соответствующий образ.

2Доказать, что функция w = z2 +5z −7 является аналитической на всей комплексной плоскости.

3Найти образ прямой x + y =1 при отображении w = z2 .

4Найти линейное отображение с неподвижной точкой z1 =1 −i , пе-

реводящее точку z2 =5i в точку w = −1 +i .

5 Вычислить ∫(2z +1)zdz , где путь интегрирования C – окружность

z =1.

6 Разложить в ряд Лорана функцию ( 1 ) по степеням z −1 и най- z z −1

ти область сходимости ряда.

		=∫1 2	e	z
7 С помощью вычетов вычислить интеграл	z				dz .
			z (z	+1)2

Найти и построить область плоскости w ,

на

которую дробно-

линейная функция w =

отображает верхний полукруг

z −1

<1 плос-

z −2

кости z .

5 Вычислить ∫z zdz , где путь интегрирования C – дуга окружности

=1,

0 ≤ arg z ≤π .

∞

Определить область сходимости ряда ∑(−1)n

ln n

n=1

n 2

С помощью вычетов вычислить интеграл ∫

dz .

=4 sin z

Вариант 13

1 Функция w = z2 отображает гиперболу xy =1 плоскости z на плос-

кость w . Найти соответствующий образ.

2 Проверить выполнимость условий Коши-Римана для функции w =sin z и найти коэффициент растяжения и угол поворота в точке z0 = π2 .

Найти образ окружности x2 + y2 =1 при отображении w = 2z +1.

Найти дробно-линейную функцию, отображающую круг

<1 на

полуплоскость

Im w > 0 так, чтобы точки z1 = −1,

z2 =1,

z3 =i

границы

=1перешли

соответственно в точки w1 = ∞,

w2 = 0,

w3 =1

границы

Im w = 0 .

Вычислить ∫(2 −3z + z2 )dz , где путь интегрирования C

– произ-

вольная линия, соединяющая точки z = 2e−π3 i и

= 2eπ3 i .

∞

z +

1−i

Определить область сходимости ряда ∑

n=1

n +i

С помощью вычетов вычислить интеграл

∫

tgz

dz .

Вариант 14

z+2

=1 z + 2

Функция w = z2 отображает окружность

x2 + y2 = 4 на плоскость

w . Найти соответствующий образ.

2 Проверить выполнимость условий Коши-Римана для функции w = cos z и найти коэффициент растяжения и угол поворота в точке z0 =π .

Пример 4. Проверить, что функция u = x2 − y2 −5x + y +2 является действительнойчастьюнекоторойаналитическойфункции f (z) инайти f (z).

Решение	∂2u		∂2u
Так как	∂2u	+	∂2u	= 2 −2 = 0 , то u (x, y) – гармоническая на всей
	∂x2		∂y2
плоскости функция. Следовательно, по формуле (3) имеем
					(x, y)
		v(x, y)=			∫ (2 y −1)dx +(2x −5)dy .
				(x0 , y0 )

Если в качестве пути интегрирования взять ломаную со звеньями, параллельными осям координат, то

x	y
v(x, y)= ∫	(2 y0 −1)dx + ∫(2x −5)dy =(2 y0 −1)(x − x0 )+(2x −5)(y − y0 )=
x0	y0
	= 2xy − x −5y +5y0 + x0 −2x0 y0 ;
	v(x, y)= 2xy − x −5y +C .
	f (z)= x2 − y2 −5x + y + 2 +i(2xy − x −5y +C )=

=(x2 −2ixy − y2 )−5(x +iy)+(−ix + y)+ 2 +Ci = z2 −5z −iz + 2 +Ci ;

f(z)= z2 −5z −iz + 2 +Ci .

1.3Конформные отображения

Если аналитическая в области D функция f (z) однолистна в этой области, т. е. для любых z1 ≠ z2 из D f (z1 )≠ f (z2 ), то она называется ре-

гулярной в этой области.

Отображение, задаваемое регулярной в области D функцией, обладает следующими свойствами:

1) всякую область Q D отображение f (z) переводит в область Q′ на плоскости (w), причём граница области Q переходит в границу области Q′ с сохранением направления обхода. Последнее означает, что если точка z пробегает границу так, что Q остаётся слева, то точка f (z) пробегает границу области Q′ так, что Q′ тоже остаётся слева;

2) всякая гладкая кривая γ из области D отображается в гладкую

кривую γ′ в области D′;

3) пусть f ′(z0 )≠ 0 для z0 D , тогда f ′(z0 ) геометрически равен коэффициенту растяжения в точке z0 при отображении f (z);

4) аргумент производной ϕ = arg f ′(z0 ) геометрически равен углу, на который нужно повернуть касательную в точке z0 к любой кривой, проходящей через точку z0 , чтобы получить касательную в точке w0 = f (z0 ) к образу γ′ этой кривой при отображении w = f (z).

Отображение, обладающее свойствами 3 и 4, называется конформным в точке z0 . Следовательно, регулярная функция, производная которой

не обращается в нуль, осуществляет конформное отображение. Более того, отображение области D , задаваемое функцией w = f (z) тогда, и только

тогда, является конформным во всех точках области, когда f (z) – регулярная в данной области функция и f ′(z)≠ 0 всюду в D .

Пример 5. Найти область конформности отображения w = z2 в пря-

моугольнике Q ={(x, y)

0 ≤ x ≤ 2,0 ≤ y ≤1}

и найти образ Q при этом ото-

бражении.

Решение

Так как (z2 )′ = 2z , то w = z2 аналитична всюду на Q . Пусть z1 ≠ z2 , а

z12 = z22

из Q .

Тогда

z12 − z22 = 0 , т. е. (z1 − z2 )(z1 + z2 )= 0 или z1 = −z2 , что

невозможно для области Q .

Следовательно, функция

w = z2

регулярна

всюду на Q .

Так как (z2 )′ = 2z = 0 только для

z = 0 , то конформность нашего

отображения нарушается только в точке z = 0 .

Найдём теперь образ границы множества Q при отображении, зада-

ваемом

функцией

w = z2 .

Согласно

примеру

u (x, y)= x2 − y2 ,

v(x, y)= 2xy .

Когда точка z

пробегает прямые

x = 2

( 0 ≤ y ≤1) и y =1

( 0 ≤ x ≤ 2), то

образ

w = z2

пробегает

параболы

u = 4 −

( 0 ≤ v ≤ 4 ),

u =

−1 ( 0 ≤ v ≤ 4 ) (рисунок 2). А когда точка z

пробегает прямые x = 0

то её образ w = z2

( 0 ≤ y ≤1) и y = 0 ( 0 ≤ x ≤ 2),

пробегает прямую v = 0

( −1 ≤u ≤ 2 ). Учитывая направление обхода границы множества Q и её об-

раза при нашем отображении, заключим, что кривосторонний треугольник ABC на плоскости w является искомым образом треугольника Q.

5 Вычислить ∫(z + 2z )dz , где путь интегрирования C – дуга окруж-

ности

= 2 , −π ≤ arg z ≤ π .

∞

(iz)−n .

Определить область сходимости ряда ∑en

n=1

С помощью вычетов вычислить интеграл ∫z sin

dz , где

C – пря-

моугольник с вершинами в

точках

z1 =1+i ,

z2 = −1 +i ,

z3 =1−2i ,

z4 = −1 −2i .

Вариант 11

Функция w = z2

отображает прямую

x = 2

плоскости

на плос-

кость w . Найти соответствующий образ.

Проверить выполнимость

условий

Коши-Римана для

функции

w = z3

и найти коэффициент растяжения и угол поворота в точке z0 =1 +i .

Найти и построить образ параболы y = x2 при отображении w = 1 .

Найти целую линейную функцию, отображающую треугольник с

вершинами в точках −4 ,

0, −6i

в плоскости z на подобный ему треуголь-

ник с вершинами в точках 1+i ,

4 +i , 4 +3i в плоскости w .

Вычислить ∫(z +5)cos zdz ,

где путь интегрирования

– произ-

z1 = 0 и z2 = 2i .

вольная линия, соединяющая точки

Разложить в ряд Тейлора функцию sin2 z

по степеням z

и найти

радиус сходимости ряда.

С помощью вычетов вычислить интеграл

∫

dz .

=3 z

+ 4)

Вариант 12

z+2i

Функция w = z2

отображает прямую

y =1 плоскости

на плос-

кость w . Найти соответствующий образ.

Проверить выполнимость

условий

Коши-Римана для

функции

w = 1z и найти коэффициент растяжения и угол поворота в точке z0 = −i . 3 Найти линейное отображение с неподвижной точкой z1 =1−i , пе-

реводящее точку z2 = −2i в точку w = 2 .

Вариант 9

1 Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству 2 < z −1+ 2i < 4 .

2	Проверить		выполнимость условий Коши-Римана для функции
w = f (z)=u +iv		и найти коэффициент растяжения и угол поворота в за-
данной	точке	z0	при отображении w = f (z), если u = x2 + 2x − y2 ,
v = 2xy + 2 y , z0 =i .

3 Найти линейную функцию, отображающую треугольник с вершинами в точках 1+i , 1+3i , 3 +i в плоскости z на подобный ему треугольник с вершинами в точках 0 , 1, i в плоскости w .

4 Для отображения w = 1z найти образ пучка прямых y = kx .

5 Вычислить ∫1 z dz , если путём интегрирования служат: а) прямоли-

−1

нейный отрезок, соединяющий точку z1 = −1 с точкой z2 =1; б) верхняя половина окружности радиуса один; в) нижняя половина этой окружности.

6 Разложить в ряд Тейлора функцию	cos2 iz			по степеням z и найти
радиус сходимости ряда.	2
радиус сходимости ряда.						ez
7 С помощью вычетов вычислить интеграл ∫						ez			dz .
7 С помощью вычетов вычислить интеграл ∫					2	(z	2	−9)	dz .
		z	=1 z
		z	=1 z

Вариант 10
1	Изобразить на комплексной плоскости множество точек, удовле-
творяющих неравенству			z −1	+	z −3	<3 .
2	Проверить выполнимость условий Коши-Римана						для функции
w = f (z)=u +iv		и найти коэффициент растяжения и угол поворота в за-
данной	точке	z0 при	отображении w = f (z), если				u = e−1−y cos x ,
v = e−1−y sin x , z0 =π −i .

3 В какие линии на плоскости w преобразуются оси координат плоскости z функцией w =iz −2 ?

4 Найти дробно-линейную функцию, отображающую круг z <1 в

круг w −1 <1 так, чтобы точки z1 = −1, z2 =i , z3 =1 границы z =1перешли соответственно в точки w1 = 0 , w2 = 2 , w3 =i +1 границы w −1 =1.

y						v
y						v

x		u

Рисунок 2

Замечание – Так как конформность рассмотренного отображения нарушена в точке z = 0 , то теперь ясно, почему прямые x = 0 и y = 0 ортого-

нальны, а их образы – нет.

Примером отображения, конформного во всей комплексной плоско-

сти z, является	отображение,	осуществляемое	линейной	функцией
w = az +b ( a ≠ 0 ). В самом деле		′
w = az +b ( a ≠ 0 ). В самом деле		w = a ≠ 0 всюду на плоскости z. Указан-
ное отображение представляет собой композицию растяжения				w1 =	a	z ,
ное отображение представляет собой композицию растяжения				w1 =	a	z ,
поворота w = ei arg a w и параллельного переноса w = w +b .
2	1	3	2

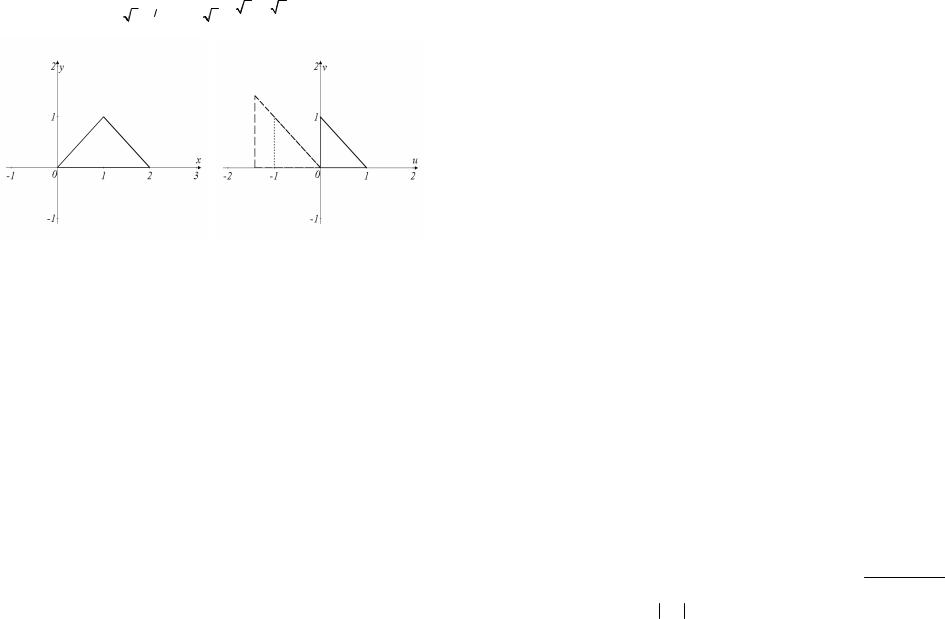
Пример 6. Построить линейную функцию, отображающую треугольник с вершинами 0 , 2 , 1+i в плоскости z на треугольник с вершинами 0 , 1, i в плоскости w.

Решение

Для удобства совместим плоскости z и w. Заметим, что треугольник с вершинами 0, 2 , 1+i подобен треугольнику с вершинами 0, 1, i , причём

коэффициент подобия k = 2 . Совершим последовательные преобразова-

ния: а) w1 = e3πi4 z – поворот вокруг начала координат на угол α = 34π

против часовой стрелки; б) w2 = 2 w1 – гомотетия (сжатие) с коэффици-

ентом k = 12 ; в) w3 = w2 +1 – параллельный перенос на вектор, изобра-

жающий число 1 (рисунок 3). В результате треугольник с вершинами 0 , 2 , 1+i отображается на треугольник с вершинами 0 , 1, i , а осуществляющая это отображение целая линейная функция имеет вид:

3πi 4

= (−1 + i)z +1.

w = w3 ow2 ow1 = 2e

z +1

−

+ i

z +1




	x				u

Рисунок 3

Другим важным примером конформного отображения расширенной плоскости (z) является отображение, осуществляемое дробно-линейной

функцией w = czaz ++db , ad −bc ≠ 0 , c ≠ 0 . При этом бесконечно удалённая

точка z = ∞ отображается в точку w = ac , а точка z = −dc переходит в бес-

конечно удалённую точку w = ∞. Дробно-линейное отображение обладает следующими свойствами:

1)каждая прямая и каждая окружность плоскости z отображаются в прямую или окружность плоскости w;

2)дробно-линейное отображение однозначно определяется заданием образов трёх точек z1 a w1 , z2 a w2 , z3 a w3 :

w − w1	w3 − w2		=	z − z1			z3 − z2		,	(4)

w − w w		− w z − z			2		z	− z
2	3	1				3		1

причём, если одна из точек z1 , z2 , z3 либо w1 , w2 , w3 является бесконечно

удалённой, то в формуле (4) все отношения, содержащие эту точку, следует заменить единицей.

Пример 7. Найти дробно-линейное отображение, преобразующее окружность C1, проходящую через точки 0 , 1, i в окружность C2, проходящую через точки −i , 0 , 1, и переводящее точки 0, 1, i соответственно в точки −i , 0 , 1. Выяснить, во что преобразуется круг, ограниченный окружностью C1.

границы Re w = 0 .

5 Вычислить ∫zdz , где путь C – это: а) прямолинейный отрезок, со-

единяющий точку z1 = 0 с точкой z2 =1+i ; б) ломанная, соединяющая точ-

ки z1 = 0 , z2 =1, z3 =1 +i .

∞

−n

6 Определить область сходимости ряда ∑

(z −2 −i)

n=1

С помощью вычетов вычислить интеграл ∫

tgz

dz , где C – ромб с

C z −1

вершинами в точках

z1 = 2, z2 =i , z3 = −2 , z4 = −i .

Вариант 8

Начертить в комплексной плоскости линию, точки которой удовле-

творяют уравнению

z +1

z −2

=5 .

Проверить

выполнимость условий Коши-Римана для функции

w = f (z)=u +iv

и найти коэффициент растяжения и угол поворота в за-

данной

точке

при отображении w = f (z),

если u = e1+2 y cos 2x ,

v = −e1+2 y sin 2x , z0 = π6 .

3 В какие линии в плоскости w отобразит функция

w = z2

прямые

x =1 и y = 2 , лежащие в плоскости z ?

4 Найти дробно-линейную функцию, отображающую круг

<1 на

полуплоскость

Im w > 0 так, чтобы точки z1 = −1,

z2 =1,

z3 =i

границы

=1перешли

соответственно в точки w1 = ∞,

w2 = −1, w3 = 2

границы

Im w = 0 .

2∫+i Re zdz , если путём интегрирования служат: а) прямо-

5 Вычислить

линейный отрезок

z =(2 +i)t , ( 0 ≤t ≤1); б) ломанная, первое звено кото-

рой есть прямолинейный отрезок [0;2], а второе – отрезок [2;2 +i].

∞

2 n

∞ z

6 Определить область сходимости ряда ∑

+ ∑

n=1 z

n=0 4

7 С помощью вычетов вычислить интеграл C∫(z +1)2 (z2 +9)dz , где

C – окружность z +1 = 2 .

1 / 21 2 > Следующая >>>

Соседние файлы в папке универ

#
29.02.2016831.09 Кб27Высшая математика.pdf
#
29.02.2016692.8 Кб23Высшая математика.Вар.индив.заданий.pdf
#
29.02.2016411.26 Кб15Высшая математика.Контр. работа №2.pdf
#
29.02.20161.31 Mб24Высшая математика.Линейное преобразование.pdf
#
29.02.2016705.23 Кб17Высшая математика.№3.pdf
#
29.02.2016446.4 Кб24Высшая математикака.Метод. указ. и инд. задания.pdf
#
29.02.20161.29 Mб39Гісторыя Беларусі.Статуты ВКЛ.pdf
#
29.02.2016375.53 Кб18Истор. Белар. Метод.указ. к сам. раб.заочн.Ч.1.2011.pdf
#
29.02.2016400.8 Кб56История Беларуси.Этнические процессы на территории Беларуси.pdf
#
29.02.2016355.69 Кб18История Беларуси. Метод. реком. Ч.1.pdf
#
29.02.2016967 Кб16История Беларуси. Метод. указ. Ч.2.pdf