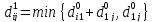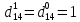1.2. Алгоритмы поиска всех кратчайших путей
В предыдущем разделе была рассмотрена задача нахождения на графе кратчайшего пути из некоторой выделенной вершины до любой другой вершины. В данном разделе будет рассмотрена задача поиска на графе кратчайшего пути между каждой парой вершин. Конечно, эта более общая задача могла бы быть решена путем многократного применения алгоритма Дейкстры с последовательным выбором каждой вершины графа в качестве вершины s. Однако реализация соответствующей процедуры потребовала бы сравнительно больших вычислительных затрат. К счастью, существуют алгоритмы более эффективные, чем процедура многократного повторения алгоритма Дейкстры. Далее рассматриваются два весьма схожих алгоритма поиска на графе кратчайших путей между всеми парами вершин. Эти алгоритмы принадлежат Флойду и Данцигу. В обоих алгоритмах для длин дуг допускаются отрицательные значения, однако не допускается наличие контуров отрицательной длины.
Пример 1. Предположим, что авиакомпания, фигурировавшая в примере 2 разд. 3.1, должна для многочисленных пассажиров ежедневно разрабатывать маршруты полетов между различными городами. Эта авиакомпания в целях экономии своих затрат стремится предоставлять пассажирам наиболее короткие маршруты. Поэтому ей хотелось бы заранее знать кратчайшие маршруты между каждой парой городов США, если, например, речь идет о полетах в пределах США.
Прежде
чем представлять алгоритмы, необходимо
ввести некоторые обозначения.
Перенумеруем вершины исходного графа
целыми числами от 1 до N.
Обозначим
через
 длину
кратчайшего пути из вершины i
в
вершину j,
который
в качестве промежуточных может
содержать только первые m
вершин
графа. (Напомним, что промежуточной
вершиной пути является любая принадлежащая
ему вершина, не совпадающая с его
начальной или конечной вершинами). Если
между вершинами i
и
j
не существует ни одного пути указанного
типа, то условно будем считать, что
длину
кратчайшего пути из вершины i
в
вершину j,
который
в качестве промежуточных может
содержать только первые m
вершин
графа. (Напомним, что промежуточной
вершиной пути является любая принадлежащая
ему вершина, не совпадающая с его
начальной или конечной вершинами). Если
между вершинами i
и
j
не существует ни одного пути указанного
типа, то условно будем считать, что
 .
Из данного определения величин
.
Из данного определения величин следует,
что величина
следует,
что величина
 представляет
длину кратчайшего пути из вершины i
в
вершину j,
не имеющего промежуточных вершин, т. е,
длину кратчайшей дуги, соединяющей i
с
j
(если такие дуги присутствуют в графе).
Для любой вершины i
положим
представляет
длину кратчайшего пути из вершины i
в
вершину j,
не имеющего промежуточных вершин, т. е,
длину кратчайшей дуги, соединяющей i
с
j
(если такие дуги присутствуют в графе).
Для любой вершины i
положим
 .
Отметим далее, что величина
.
Отметим далее, что величина
 представляет
длину кратчайшего пути между вершинами
i
и
j.
представляет
длину кратчайшего пути между вершинами
i
и
j.
Обозначим
через
 матрицу
размера
матрицу
размера
 ,
элемент
(i,
j)
которой совпадает с
,
элемент
(i,
j)
которой совпадает с
 . Если
в исходном графе нам известна длина
каждой дуги, то мы можем сформировать
матрицу
. Если
в исходном графе нам известна длина
каждой дуги, то мы можем сформировать
матрицу
 .
Наша
цель состоит в определении матрицы
.
Наша
цель состоит в определении матрицы
 ,
представляющей кратчайшие пути между
всеми вершинами рассматриваемого графа.
,
представляющей кратчайшие пути между
всеми вершинами рассматриваемого графа.
В
алгоритме Флойда в качестве исходной
выступает матрица
 .
Вначале
из этой матрицы вычисляется матрица
.
Вначале
из этой матрицы вычисляется матрица
 .
Затем
по матрице
.
Затем
по матрице
 вычисляется матрица
вычисляется матрица
 и т. д. Процесс повторяется до тех пор,
пока по матрице
и т. д. Процесс повторяется до тех пор,
пока по матрице не будет вычислена матрица
не будет вычислена матрица .
.
Рассмотрим основную идею, лежащую в основе алгоритма Флойда. Предположим, что нам известны:
а) кратчайший путь из вершины i в вершину т, в котором в качестве промежуточных допускается использование только первых (т — 1) вершин;
б) кратчайший путь из вершины т в вершину j, в котором в качестве промежуточных допускается использование только первых (т — 1) вершин;
в) кратчайший путь из вершины i в вершину j, в котором в качестве промежуточных допускается использование только первых (m — 1) вершин.
Поскольку по предположению исходный граф не может содержать контуров отрицательной длины, один из двух путей — путь, совпадающий с представленным в п. «в», или путь, являющийся объединением путей из пп. «а» и «б», —должен быть кратчайшим путем из вершины i в вершину j, в котором в качестве промежуточных допускается использование только первых т вершин. Таким образом,
 (3)
(3)
Из
соотношения (3)
видно,
что для вычисления элементов матрицы
 необходимо
располагать лишь элементами матрицы
необходимо
располагать лишь элементами матрицы
 .Более
того, соответствующие вычисления могут
быть проведены без обращения к исходному
графу. Теперь мы в состоянии дать
формальное описание алгоритма Флойда
для нахождения на графе кратчайших
путей между всеми парами вершин.
.Более
того, соответствующие вычисления могут
быть проведены без обращения к исходному
графу. Теперь мы в состоянии дать
формальное описание алгоритма Флойда
для нахождения на графе кратчайших
путей между всеми парами вершин.
Алгоритм Флойда
Шаг
1.
Перенумеровать
вершины исходного графа целыми числами
от 1 до N.
Определить
матрицу
 ,
задав
величину каждого ее элемента (i,j)
равной
длине кратчайшей дуги, соединяющей
вершину i
с
вершиной
j.
Если в исходном графе указанные вершины
не соединяются дугами, положить
,
задав
величину каждого ее элемента (i,j)
равной
длине кратчайшей дуги, соединяющей
вершину i
с
вершиной
j.
Если в исходном графе указанные вершины
не соединяются дугами, положить
 .
Кроме того, для всех
.
Кроме того, для всех
i
положить
 .
.
Шаг
2.
Для
целого т,
последовательно
принимающего значения
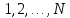 ,
определить
по величинам элементов матрицы
,
определить
по величинам элементов матрицы
 величины
элементов матрицы
величины
элементов матрицы
 ,
используя
рекурсивное соотношение (3), т. е.
соотношение
,
используя
рекурсивное соотношение (3), т. е.
соотношение

При
определении величины каждого элемента
матрицы
 фиксировать
соответствующий кратчайший путь.
фиксировать
соответствующий кратчайший путь.
По
окончании данной процедуры величина
элемента (i,
j)
матрицы
 определяет
длину кратчайшего пути, ведущего из
вершины i
в
вершину j.
определяет
длину кратчайшего пути, ведущего из
вершины i
в
вершину j.
То, что описанный алгоритм действительно находит кратчайшие пути, может быть индуктивно доказано на основе следующего факта. Длина кратчайшего пути из вершины i в вершину j, допускающего использование в качестве промежуточных первых m вершин, должна быть не больше длины кратчайшего пути из i в j, допускающего использование в качестве промежуточных первых (m — 1) вершин, и не больше длины кратчайшего пути из i в j, допускающего использование в качестве промежуточных первых (т — 1) вершин и обязательно — вершины т.
Отметим,
что для всех i
и
т
должно
быть
 .
Поэтому нет необходимости в вычислении
диагональных элементов матриц
.
Поэтому нет необходимости в вычислении
диагональных элементов матриц
 .
Кроме
того, для всех
.
Кроме
того, для всех
 имеют
место соотношения
имеют
место соотношения
 и
и
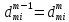 .
Эти
соотношения обусловливаются тем,
что вершина т
в
отсутствие контуров отрицательной
длины не может выступать в качестве
промежуточной в любых кратчайших путях,
которые начинаются или заканчиваются
в самой вершине т.Следовательно,
при определении матрицы
.
Эти
соотношения обусловливаются тем,
что вершина т
в
отсутствие контуров отрицательной
длины не может выступать в качестве
промежуточной в любых кратчайших путях,
которые начинаются или заканчиваются
в самой вершине т.Следовательно,
при определении матрицы
 нет
необходимости в пересчете элементов
m-й
строки и т-ого
столбца
матрицы
нет
необходимости в пересчете элементов
m-й
строки и т-ого
столбца
матрицы
 .
Таким образом, в матрице
.
Таким образом, в матрице по
формуле (3) необходимо считать лишь
величины
по
формуле (3) необходимо считать лишь
величины
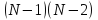 элементов, в число которых не входят
диагональные элементы, а также элементы
изm-й
строки
и m-го
столбца.
элементов, в число которых не входят
диагональные элементы, а также элементы
изm-й
строки
и m-го
столбца.
Пример
2.
(Применение алгоритма Флойда). Для
графа,
изображенного на рис. 3.1,
матрица
 ,
составленная
из длин дуг графа,такова:
,
составленная
из длин дуг графа,такова:

Величины
элементов матрицы
 и соответствующие им кратчайшие пути
определяются следующим образом:
и соответствующие им кратчайшие пути
определяются следующим образом:
|
|
Соответствующие пути |
|
|
(1,2) (1,3) (1,4) (2,1)
(2,1),(1,3) (2,1),(1,4) (3,1) (3,2)
(3,4) (4,1) (4,1),(1,2) (4,1),(1,3) |
Аналогичным
образом могут быть определены величины
элементов матриц
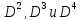 и соответствующие им кратчайшие пути.
Полученные результаты приводятся ниже.
и соответствующие им кратчайшие пути.
Полученные результаты приводятся ниже.
Матрица
 :
:

Кратчайшие
пути для элементов матрицы
 :
:

Матрица
 :
:

Кратчайшие
пути для элементов матрицы
 :
:

Матрица
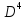 :
:
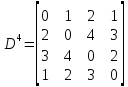
Кратчайшие
пути для элементов матрицы
 :
:

Заметим, что при произвольной нумерации вершин исходного графа в процессе выполнения алгоритма кратчайшего пути будут отыскиваться на более ранних стадиях для тех вершин, которые, имея близкие номера, являются «близкими» и по длинам соответствующих кратчайших путей.
В представленном выше численном примере кратчайшие пути между соответствующими вершинами формировались по мере выполнения процедуры алгоритма. Очевидно, для задач реальных размерностей такой способ формирования кратчайших путей является практически малопригодным. Следовательно, необходимо, разработать более эффективный способ определения дуг, составляющих кратчайший путь.
Введем
в рассмотрение предпоследние вершины
путей. Пусть
 обозначает
предпоследнюю вершину кратчайшего
пути, соединяющего вершину i
с
вершиной j.
(Если между указанными вершинами имеется
несколько соединяющих их кратчайших
путей, то для пары (i,
j)
может
существовать несколько предпоследних
вершин. В этом случае через
обозначает
предпоследнюю вершину кратчайшего
пути, соединяющего вершину i
с
вершиной j.
(Если между указанными вершинами имеется
несколько соединяющих их кратчайших
путей, то для пары (i,
j)
может
существовать несколько предпоследних
вершин. В этом случае через
 следовало
бы обозначать множество всех этих
вершин. Однако если нас интересует
только один кратчайший путь, то можно
ограничить рассмотрение лишь одной из
вершин, составляющих множество
следовало
бы обозначать множество всех этих
вершин. Однако если нас интересует
только один кратчайший путь, то можно
ограничить рассмотрение лишь одной из
вершин, составляющих множество
 ).
Если
).
Если
 известно
для каждой пары вершин i
и
j,
то все промежуточные вершины кратчайшего
пути из i
в
j
могут
быть определены следующим образом.
Пусть предпоследней вершиной искомого
пути является вершина k,
т.
е.
известно
для каждой пары вершин i
и
j,
то все промежуточные вершины кратчайшего
пути из i
в
j
могут
быть определены следующим образом.
Пусть предпоследней вершиной искомого
пути является вершина k,
т.
е.
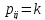 .Тогда
вторая от конца вершина на этом пути
является предпоследней вершиной
кратчайшего пути из i
в k,
т. е. совпадает с
.Тогда
вторая от конца вершина на этом пути
является предпоследней вершиной
кратчайшего пути из i
в k,
т. е. совпадает с
 .
Данную
процедуру можно повторять и далее
до тех пор, пока не будет пройден в
обратном направлении весь кратчайший
путь из вершины i
в
вершину j.
Таким
образом, для того, чтобы определить
кратчайшие пути между всеми парами
вершин, необходимо располагать лишь
элементами
.
Данную
процедуру можно повторять и далее
до тех пор, пока не будет пройден в
обратном направлении весь кратчайший
путь из вершины i
в
вершину j.
Таким
образом, для того, чтобы определить
кратчайшие пути между всеми парами
вершин, необходимо располагать лишь
элементами
 для
всех пар вершин (i,
j).
для
всех пар вершин (i,
j).
Существуют
два способа определения
 —
встроенный
(tentative)
и внешний
(terminal).
Опишем
каждый из них в отдельности.
—
встроенный
(tentative)
и внешний
(terminal).
Опишем
каждый из них в отдельности.
Встроенный способ. Перед началом работы алгоритма Флойда (точнее, перед шагом 2) в качестве
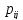 принять
элемент i
(это
проделать для каждого j).
Далее в процессе выполнения алгоритма
при использовании соотношения (3) каждый
раз фиксировать, какая из величин
принять
элемент i
(это
проделать для каждого j).
Далее в процессе выполнения алгоритма
при использовании соотношения (3) каждый
раз фиксировать, какая из величин
 или
или меньше.
Как только меньшей оказывается
первая из этих величин, положить
меньше.
Как только меньшей оказывается
первая из этих величин, положить
 равным
т.
В
противном случае оставить
равным
т.
В
противном случае оставить
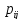 неизменным.
(Если оказывается, что величины, входящие
в правую часть соотношения (3), одинаковы,
то можно либо не менять
неизменным.
(Если оказывается, что величины, входящие
в правую часть соотношения (3), одинаковы,
то можно либо не менять
 ,
либо
принять его равным т).
,
либо
принять его равным т).
После
окончания выполнения алгоритма элементы
 ,
сформированные
данным способом, действительно определяют
предпоследние вершины кратчайших
путей, ведущих из вершины i
в
вершину j.
,
сформированные
данным способом, действительно определяют
предпоследние вершины кратчайших
путей, ведущих из вершины i
в
вершину j.
Внешний способ. Считая работу алгоритма Флойда законченной, а значит, и зная матрицу
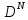 ,определить
каждое
,определить
каждое
 ,
положив
его равным любому k,
для
которого
,
положив
его равным любому k,
для
которого
 ;
при
этом для формирования
;
при
этом для формирования
 требуются
только матрицы D0
и
DN.
требуются
только матрицы D0
и
DN.
Отметим,
что в ситуации, когда алгоритм Флойда
уже выполнен, единственное, что остается
сделать для определения кратчайших
путей, — это воспользоваться внешним
способом формирования
 .
Если
же заранее известно, что необходимо
определить не только длины кратчайших
путей, но и сами пути, то, безусловно,
лучше применять встроенный способ,
поскольку реализация его в рамках
основного алгоритма лишь незначительно
увеличивает объем вычислений.
.
Если
же заранее известно, что необходимо
определить не только длины кратчайших
путей, но и сами пути, то, безусловно,
лучше применять встроенный способ,
поскольку реализация его в рамках
основного алгоритма лишь незначительно
увеличивает объем вычислений.
Еще один алгоритм поиска на графе кратчайших путей между всеми парами вершин был предложен Данцигом. Алгоритм Данцига весьма близок к алгоритму Флойда и отличается от последнего лишь иным порядком выполнения тех же самых операций.
Итак,
рассмотрим алгоритм Данцига. Снова
перенумеруем вершины исходного графа
целыми числами от 1 до N
и
обозначим через
 длину
кратчайшего пути из
вершины
i
в
вершину j,
в котором допускается использование в
качестве промежуточных т
первых
вершин графа. Пусть теперь в отличие от
алгоритма Флойда матрица
длину
кратчайшего пути из
вершины
i
в
вершину j,
в котором допускается использование в
качестве промежуточных т
первых
вершин графа. Пусть теперь в отличие от
алгоритма Флойда матрица
 ,
состоящая
из величин
,
состоящая
из величин
 ,
при
каждом
,
при
каждом
 имеет
размерность не
(NхN),
а
(т
х
т).
Так
же, как и раньше, требуется определить
матрицу
имеет
размерность не
(NхN),
а
(т
х
т).
Так
же, как и раньше, требуется определить
матрицу
 ,элемент
(i,
j)
которой определяет длину кратчайшего
пути из вершины i
в
вершину j.
Как и в алгоритме Флойда, в алгоритме
Данцига матрица
,элемент
(i,
j)
которой определяет длину кратчайшего
пути из вершины i
в
вершину j.
Как и в алгоритме Флойда, в алгоритме
Данцига матрица
 определяется
из матрицы
определяется
из матрицы
 ,
матрица
,
матрица из
матрицы
из
матрицы
 и
т. д. Наконец, матрица
и
т. д. Наконец, матрица
 определяется
из матрицы
определяется
из матрицы
 .
.
В
чем же идея алгоритма Данцига? Во-первых,
отметим, что каждая новая вычисляемая
матрица
 содержит
на одну строку и на один столбец больше,
чем ее предшественница, матрица
содержит
на одну строку и на один столбец больше,
чем ее предшественница, матрица
 .
Элементы матрицы
.
Элементы матрицы ,
не
входящие в последние строку и столбец
(число таких элементов равно
,
не
входящие в последние строку и столбец
(число таких элементов равно
 ,
определяются точно так же, как в алгоритме
Флойда. Что же касается остальных
элементов
,
определяются точно так же, как в алгоритме
Флойда. Что же касается остальных
элементов ,
где
,
где
 или.
или. ,
то
они определяются с учетом приводимых
ниже соображений. Кратчайший путь из
вершины i
в
вершину т
(или
наоборот), в котором допускается
использование в качестве промежуточных
только первых т
вершин
графа, не может иметь среди промежуточных
вершину т,
поскольку
любой контур в исходном графе имеет
неотрицательную длину. В силу данного
обстоятельства такой кратчайший путь
из вершины i
в
вершину т
должен
иметь своей первой частью кратчайший
путь из вершины i
в
некоторую вершину
,
то
они определяются с учетом приводимых
ниже соображений. Кратчайший путь из
вершины i
в
вершину т
(или
наоборот), в котором допускается
использование в качестве промежуточных
только первых т
вершин
графа, не может иметь среди промежуточных
вершину т,
поскольку
любой контур в исходном графе имеет
неотрицательную длину. В силу данного
обстоятельства такой кратчайший путь
из вершины i
в
вершину т
должен
иметь своей первой частью кратчайший
путь из вершины i
в
некоторую вершину
 ,
который
допускает использование в качестве
промежуточных только
,
который
допускает использование в качестве
промежуточных только
 первых вершин графа, а второй частью —
кратчайшую дугу, ведущую из вершиныj
в вершину т
(конечно,
следует рассматривать только такие
вершины j,
для которых имеется хотя бы одна дуга,
ведущая из
j
в
т).
Аналогично
кратчайший путь из вершины т
в
вершину
i,
в котором допускается использование в
качестве промежуточных только т
первых
вершин графа, должен иметь своей первой
частью кратчайшую дугу, ведущую из
вершины т
в
некоторую
вершину
первых вершин графа, а второй частью —
кратчайшую дугу, ведущую из вершиныj
в вершину т
(конечно,
следует рассматривать только такие
вершины j,
для которых имеется хотя бы одна дуга,
ведущая из
j
в
т).
Аналогично
кратчайший путь из вершины т
в
вершину
i,
в котором допускается использование в
качестве промежуточных только т
первых
вершин графа, должен иметь своей первой
частью кратчайшую дугу, ведущую из
вершины т
в
некоторую
вершину
 ,
а
второй частью — кратчайший путь из
вершины j
в. вершину i,
который допускает использование в
качестве промежуточных только (т
—
1)
первых
вершин (конечно, следует рассматривать
только такие вершины j,
для которых имеется хотя бы одна дуга,
ведущая из m
в
j).
Наконец, отметим, что величины
,
а
второй частью — кратчайший путь из
вершины j
в. вершину i,
который допускает использование в
качестве промежуточных только (т
—
1)
первых
вершин (конечно, следует рассматривать
только такие вершины j,
для которых имеется хотя бы одна дуга,
ведущая из m
в
j).
Наконец, отметим, что величины
 должны
полагаться равными нулю.
должны
полагаться равными нулю.
С учетом приведенных соображений мы можем теперь формально описать алгоритм Данцига.
Алгоритм Данцига поиска всех кратчайших путей
Шаг
1.
Перенумеровать
вершины исходного графа целыми числами
от 1 до N.
Сформировать
матрицу
 (размерностью
(размерностью
 ),
каждый элемент (i,
j)
которой
),
каждый элемент (i,
j)
которой
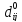 определяет
длину кратчайшей дуги, ведущей из вершины
i
в
вершину j.
В отсутствие такой дуги положить
определяет
длину кратчайшей дуги, ведущей из вершины
i
в
вершину j.
В отсутствие такой дуги положить
 .
.
Шаг
2.
Здесь
через
 обозначается
матрица размерностью
обозначается
матрица размерностью
 с элементами
с элементами .Последовательно
определить элементы матрицы
.Последовательно
определить элементы матрицы
 из
элементов матрицы
из
элементов матрицы
 для
т,
принимающего
значения
для
т,
принимающего
значения
 :
:
 (4)
(4)
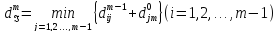 (5)
(5)
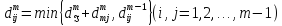 (6)
(6)
Кроме того, для всех i и т положить
 (7)
(7)
Кратчайшие
пути, длины которых определяются
величинами
 элементов
матрицы
элементов
матрицы
 ,
могут
быть определены аналогично тому, как
это делалось в алгоритме Флойда.
,
могут
быть определены аналогично тому, как
это делалось в алгоритме Флойда.
Анализ вычислительной сложности достаточно просто проводить для таких алгоритмов, в которых число выполняемых операций практически неизменно. Именно такими алгоритмами при фиксированном исходном графе являются алгоритмы Дейкстры, Флойда и Данцига. Однако существуют алгоритмы, точное число операций в которых не может быть определено заранее. Например, нельзя заранее определить число операций алгоритма Форда, поскольку нельзя до выполнения алгоритма точно указать, сколько раз будет окрашиваться каждая вершина графа. Для алгоритмов типа алгоритма Форда обычно при анализе вычислительной сложности определяют верхнюю границу возможного числа операций.
Как видно из описания алгоритмов поиска кратчайших путей, в основном они состоят из операций двух типов: операции сложения и операции сравнения по минимуму. При анализе вычислительной сложности любого из этих алгоритмов необходимо каким-либо образом выявить соотношение между вычислительными затратами на выполнение операции сложения и сравнения. Конечно, это соотношение определяется используемыми вычислительными средствами (автоматическими или ручными). Однако для большего удобства мы будем предполагать, что для выполнения обеих операций требуется одинаковое время.
Перейдем
теперь к определению числа операций в
алгоритмах Флойда (Данцига), Дейкстры
и Форда. В алгоритме Флойда вычисляются
N
матриц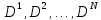 ,каждая
из которых состоит из
,каждая
из которых состоит из
 элементов.
Следовательно, в алгоритме Флойда
необходимо вычислять
элементов.
Следовательно, в алгоритме Флойда
необходимо вычислять элементов.
Каждое такое вычисление осуществляется
с помощью соотношения (3) и требует
выполнения одной операции сложения
и одной операции сравнения. Следовательно,
в алгоритме Флойда выполняется
элементов.
Каждое такое вычисление осуществляется
с помощью соотношения (3) и требует
выполнения одной операции сложения
и одной операции сравнения. Следовательно,
в алгоритме Флойда выполняется
 сложений
и
сложений
и сравнений.
(Строго говоря, указанные числа несколько
превышают действительные показатели,
поскольку некоторые элементы матрицы
сравнений.
(Строго говоря, указанные числа несколько
превышают действительные показатели,
поскольку некоторые элементы матрицы могут
быть непосредственно приравнены
соответствующим элементам из матрицы
могут
быть непосредственно приравнены
соответствующим элементам из матрицы без
проведения вычислений с помощью
соотношения (3). Это относится к
элементамi-й
строки и i-го
столбца матриц
без
проведения вычислений с помощью
соотношения (3). Это относится к
элементамi-й
строки и i-го
столбца матриц
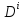 и
и
 ,
являющихся
в этих матрицах одинаковыми.) Итак, общее
количество операций, выполняемых в
алгоритме Флойда, пропорционально
,
являющихся
в этих матрицах одинаковыми.) Итак, общее
количество операций, выполняемых в
алгоритме Флойда, пропорционально
 Используя
более строгую терминологию, этот
результат можно сформулировать следующим
образом: алгоритм Флойда требует для
своего выполнения времени счета порядка0
(
Используя
более строгую терминологию, этот
результат можно сформулировать следующим
образом: алгоритм Флойда требует для
своего выполнения времени счета порядка0
( ).
).
Далее проанализируем вычислительную сложность алгоритма Дейкстры. На первой итерации этого алгоритма должны быть просмотрены (N-1) неокрашенных вершин. Поскольку просмотры вершин осуществляются с помощью уравнения (1), то на первой итерации выполняется (N-1) операций сложения, (N-1) операций сравнения, а также производится выбор наименьшего из (N-1) чисел (т. е. выполняется еще (N-1) операций сравнения). Итак, первая итерация включает 3(N-1) операций. Аналогично можно показать, что вторая итерация включает
3(N-2) операций, третья 3(N-3) операций и т. д. Общее число операций в алгоритме Дейкстры определяется соотношением

Помимо
указанных операций на каждой итерации
алгоритма необходимо также выполнять
операции по выявлению окрашенных и
неокрашенных вершин. Это, вообще говоря,
приводит к дополнительным вычислительным
затратам, которые, однако, могут быть
сведены к минимуму при использовании
соответствующих приемов реализации
алгоритма при составлении программы.
Рассмотрение этих приемов выходит
за рамки настоящей книги. Итак, алгоритм
Дейкстры имеет время счета порядка .
Отсюда можно заключить, что алгоритм
Форда в наихудшем случае имеет время
счета порядка
.
Отсюда можно заключить, что алгоритм
Форда в наихудшем случае имеет время
счета порядка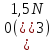 .
Действительно,
в алгоритме Дейкстры каждая вершина
окрашивается ровно один раз, а в алгоритме
Форда она может окрашиваться до (N-1)
раза.
.
Действительно,
в алгоритме Дейкстры каждая вершина
окрашивается ровно один раз, а в алгоритме
Форда она может окрашиваться до (N-1)
раза.
Таким
образом, нами получены следующие
результаты: в алгоритме Дейкстры
выполняется
 операций;
в алгоритме Форда в наихудшем случае
выполняется
операций;
в алгоритме Форда в наихудшем случае
выполняется
 операций;
в алгоритме Флойда выполняется
операций;
в алгоритме Флойда выполняется операций;
в алгоритме Данцига выполняется
операций;
в алгоритме Данцига выполняется операций.
операций.
Как
уже отмечалось, алгоритм Флойда мог бы
быть заменен алгоритмом Дейкстры,
многократно повторяемым при выборе в
качестве начальной каждой вершины
исходного графа. Соответствующая
процедура связана с затратами времени
порядка 0( ),что
меньше времени счета для алгоритма
Флойда, имеющего порядок 0(
),что
меньше времени счета для алгоритма
Флойда, имеющего порядок 0( ).Надо,
однако, иметь в виду, что при наличии в
исходном графе дуг отрицательной длины
(при этом, конечно, исключается наличие
контуров отрицательной длины), алгоритм
Дейкстры должен быть заменен алгоритмом
Форда, что приводит к времени счета
порядка 0(
).Надо,
однако, иметь в виду, что при наличии в
исходном графе дуг отрицательной длины
(при этом, конечно, исключается наличие
контуров отрицательной длины), алгоритм
Дейкстры должен быть заменен алгоритмом
Форда, что приводит к времени счета
порядка 0(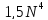 ).
Данная
оценка при достаточно большом N
превышает величину 0(
).
Данная
оценка при достаточно большом N
превышает величину 0( )
затрат
времени для алгоритма Флойда. Однако
не следует забывать, что действительно
количество операций в алгоритме Форда,
по всей вероятности, будет значительно
меньше используемой для него оценки.
)
затрат
времени для алгоритма Флойда. Однако
не следует забывать, что действительно
количество операций в алгоритме Форда,
по всей вероятности, будет значительно
меньше используемой для него оценки.