
Литература / Дополнительная литература / Зайцев Д. А. Математические модели дискретных систем
.pdf
Дерево покрывающих маркировок позволяет исследовать ряд свойств сетей Петри. Действительно, сеть Петри ограничена тогда и только тогда, когда ее дерево покрывающих маркировок не содержит символ ; сеть Петри безопасна тогда и только тогда, когда маркировки вершин ее дерева покрывающих маркировок содержат лишь числа 0 и 1. Переход пассивный (не является потенциально живым), когда его символом не обозначена ни одна из дуг дерева; если маркировка 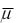 достижима в сети, то дерево покрывающих маркировок содержит такую маркировку
достижима в сети, то дерево покрывающих маркировок содержит такую маркировку 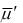 , что
, что 
 ; дерево покрывающих маркировок безтупиковой сети не содержит терминальных вершин. Кроме того, дерево покрывающих маркировок позволяет найти повторяемые и стационарно повторяемые последовательности срабатываний переходов.
; дерево покрывающих маркировок безтупиковой сети не содержит терминальных вершин. Кроме того, дерево покрывающих маркировок позволяет найти повторяемые и стационарно повторяемые последовательности срабатываний переходов.
Исследуем свойства сети N3 с помощью дерева покрывающих маркировок, изображенного на рис. 2.10:
 сеть неограниченна, так как дерево содержит символы ;
сеть неограниченна, так как дерево содержит символы ;
 сеть потенциально живая, так как содержит дуги, обозначенные символами каждого из переходов;
сеть потенциально живая, так как содержит дуги, обозначенные символами каждого из переходов;
 сеть не является живой, так как дерево содержит терминальные (тупиковые) вершины;
сеть не является живой, так как дерево содержит терминальные (тупиковые) вершины;
 маркировка (0,7,1) достижима в сети; на самом деле, дерево содержит покрывающую маркировку (0, ,1) по которой может быть построена последовательность срабатывания переходов t17t2 , которая переводит сеть в указанную маркировку; маркировка (0,1,7) недостижима в сети, так как дерево не содержит для нее покрывающую маркировку;
маркировка (0,7,1) достижима в сети; на самом деле, дерево содержит покрывающую маркировку (0, ,1) по которой может быть построена последовательность срабатывания переходов t17t2 , которая переводит сеть в указанную маркировку; маркировка (0,1,7) недостижима в сети, так как дерево не содержит для нее покрывающую маркировку;
 последовательность срабатывания t1 повторяемая;
последовательность срабатывания t1 повторяемая;  последовательность срабатывания t2t4t1t1 стационарно повторяемая.
последовательность срабатывания t2t4t1t1 стационарно повторяемая.
Итак, сети Петри является эффективным средством анализа и синтеза параллельных асинхронных систем, и имеют ряд важных преимуществ, таких как наглядное графическое представление, аналитические и имитационные методы исследования, набор расширений базовой модели с высокой изобразительной мощностью, возможность комплексной отладки модели объекта и алгоритма управления, аппаратную реализацию процессоров сетей Петри.
30

3 Машины Тюринга
3.1 Интуитивное понятие алгоритма
Использование интуитивного понятия алгоритма, вернее, первое письменное упоминание о его использовании, берет свое начало в работах узбекского математика Мухаммада ибн Мусы аль-Хорезми и датируется VIII веком. В течение следующих двенадцати веков алгоритмы успешно применялись в разных областях деятельности человека. Однако к началу XX века сформировалось множество задач, для решения которых, по представлениям ученых, не существует алгоритмов. Некоторые из таких задач упомянуты в известном списке проблем, представленном Гильбертом. Математическое доказательство алгоритмической неразрешимости требовало формализации интуитивного понятия алгоритма. Машина Тюринга и является одной из таких формализаций. Появившись практически вместе с другими моделями, такими как рекурсивные функции Клини и нормальные алгоритмы Маркова, она позволила доказать, что для целого ряда задач не существует алгоритма их решения.
Интуитивно под алгоритмом понимают точно описанный пошаговый процесс вычисления, в котором строго определен порядок выполнения шагов и на каждом шаге точно указано, как по исходным данным получить результат.
Классическим примером алгоритма является алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел a и b. Алгоритм заключается в последовательном построении разности чисел до тех пор, пока результат не совпадет с меньшим числом. Его можно сформулировать в виде такой последовательности шагов:
Шаг 0. |
Для определенности выбрать: a |
max( a, b) , b min( a, b) . |
|
Шаг 1. |
Если a b , |
то искомый наибольший общий делитель найден, и он |
|
равен, для определенности, числу a. Стоп. |
|
||
Шаг 2. |
Вычислить c |
a b. |
|
Шаг 3. |
Выбрать a |
max( b, c) , b min( b, |
c) . Перейти к шагу 1. |
Выполним алгоритм для пары чисел 275 и 150: a=275, b=150, c=125;
a=150, b=125, c=25; a=125, b=25, c=100; a=100, b=25, c=75; a=75, b=25, c=50; a=50, b=25, c=25; a=b=25.
31
Итак, наибольший общий делитель чисел 275 и 150 равняется 25.
Обоснование алгоритма Евклида базируется на известном в математике факте, что наибольший общий делитель двух чисел является также делителем их разности.
Сформулируем более подробно основные черты, присущие алгоритму:
1)Массовость. Заключается в том, что алгоритм предназначен для решения не единичной задачи (например, 2+2=?), а целой серии однотипных задач (x+y=?).
2)Детерминированность. Другими словами, - определенность, заключается в том, что после выполнения каждого из шагов мы точно знаем, какой шаг следует выполнять следующим.
3)Конструктивность. Предполагается, что алгоритм всегда выполняется за конечное количество шагов. Шагов может быть весьма много, однако общее их количество всегда конечно. При построении алгоритма мы исходим из гипотезы потенциальной осуществимости, считая, что при выполнении алгоритма мы ничем не ограничены: ни временем, ни доступными ресурсами.
4)Элементарность шагов. Каждый шаг алгоритма должны быть настолько простой, чтобы его можно было выполнить однозначно точно.
Итак, мы рассмотрели интуитивное понятие алгоритма. Изучаемая далее машина Тюринга является одной из математических моделей, предложенных для формализации этого понятия.
3.2. Описание машины Тюринга
Машина Тюринга (рис. 3.1) состоит из бесконечной в обе стороны ленты, разбитой на ячейки и управляющей головки. Головка двигается вдоль ленты. В определенный момент времени головка осматривает одну из ячеек ленты (текущую). Головка читает символ из текущей ячейки и, в зависимости от комбинации прочитанного символа и текущего состояния, вырабатывает символ, который записывает в ячейку и выполняет одно из трех действий: сдвигает на одну ячейку влево, остается на месте, сдвигает на одну ячейку вправо. Кроме этого, головка переходит в следующее состояние. Итак, элементарный шаг машины Тюринга состоит из чтения, записи, движения и перехода к следующему состоянию. Общее количество состояний и алфавит символов ленты являются конечными. Специально выделяют начальное и заключительное состояния машины.
32

лента
ячейка
|
управляющая |
|
головка |
влево |
вправо |
Рисунок 3.1 - Машина Тюринга
Предполагается, что для каждого момента времени лишь в конечном количестве ячеек записаны символы алфавита, в остальных ячейках записан специальный пустой символ  (лямбда). Наименьшую часть ленты, в которой содержатся все ячейки с символами алфавита, будем называть рабочей зоной.
(лямбда). Наименьшую часть ленты, в которой содержатся все ячейки с символами алфавита, будем называть рабочей зоной.
Для удобства считаем, что в начале работы машины и при ее завершении головка находится над самой левой ячейкой рабочей зоны. Специально задают начальное состояние машины. Работа машины длится до тех пор, пока она не попадет в заданное заключительное состояние.
Машина Тюринга, как и конечный автомат, может быть представлена диаграммой состояний или матрицей переходов. Рассмотрим указанные способы представления на следующем примере.
Пример 1. Построить машину Тюринга, которая выполняет сложение натуральных чисел в унарной системе счисления. В унарной системе счисления число n задают соответствующим количеством палочек (единиц), записанных на ленте. Для разделения чисел используем символ звездочки. Рассмотрим начальное и заключительное состояния ленты для комбинации чисел 3+4=7:
а) В начале:
… |
|
|
|
1 |
1 |
1 |
* |
1 |
1 |
1 |
1 |
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) При завершении: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
… |
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выберем такой алгоритм: сдвигаемся вправо к звездочке; заменяем звездочку на палочку; сдвигаемся влево к лямбде; заменяем крайнюю по левую сторону палочку на лямбду; останов. Диаграмма состояний машины Тюринга представлена на рис. 3.2. Таблица 3.1 содержит матричное представление машины.
33

1|1R |
|
1|1L |
|
|
|
|
|
|
|
|
|
|
|
q0 |
*|1L |
q1 |
| R |
q2 |
1| R |
q3 |
|
|
|
Рисунок 3.2 - Диаграмма состояний машины Тюринга для сложения чисел
Таблица 3.1 - Матричное представление машины Тюринга для сложения чисел
Состояние/символ |
|
1 |
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
q0 |
|
1,R, q0 |
|
|
|
1,L, q1 |
|
|
|
- |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
q1 |
|
1,L, q1 |
|
|
|
|
- |
|
|
|
,R, q2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q2 |
|
,S, q3 |
|
|
|
|
- |
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q3 |
|
- |
|
|
|
|
|
- |
|
|
|
|
- |
|
Выполним формальное теоретико-множественное определение машины |
||||||||||||||
Тюринга. Итак, машина Тюринга |
– |
это |
пятерка |
M |
(X , Q, |
q0, q f , P) , |
где |
|||||||
X {xi } – конечная алфавит |
символов ленты; |
Q |
{q j } – конечное |
множество |
||||||||||
состояний головки; q0 |
и |
q f |
– |
начальное |
и |
заключительное |
состояния |
|||||||
соответственно; P : Q X |
X |
R |
Q |
– |
программа |
машины; |
R |
{L, S, R} |
– |
|||||
допустимые перемещения головки: влево, на месте, вправо.
Построим более сложную машину Тюринга, создание которой укрепит уверенность в нашей возможности представлять таким образом произвольный алгоритм.
Пример 2. Построить машину Тюринга, которая выполняет умножение чисел в унарной системе исчисления.
Алгоритм заключается в последовательном добавлении множимого к частичному результату; количество добавлений задается множителем; для запоминания добавленной (дописанной) единицы будем использовать символ e, а для разделения множимого и результата – символ b. Опишем кратко основные шаги:
1.сдвигаемся вправо к , ставим разделитель b;
2.сдвигаемся влево к ;
3.стираем палочку первого числа (множителя); если палочки отсутствуют - идти к 5;
4.дописываем второе число (множимое) по правую сторону, переходим к 3;
5.стираем множимое и разделители.
Итак X {1,*, ,e,b}, Q {q0 ,..., q9 }, q0 q0 , q f q9 , P :
34

|
1|1R |
|
|
|
1|1L |
|
|
|
|
|
|
|
b|bR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e|eR |
|
|1L |
|
|
|
|
|
|
|
|
|
|
q5 |
q6 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
1|1R |
|
e|eL |
|
e|1R |
|
|
|
|
|
|
|
*|*R |
1|eR |
b|bL |
|
|
|
1|1L |
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
*|*L |
|
|
q3 |
b|bL |
q4 |
|
*|*R |
q7 |
b|bL |
|
q8 |
|
|
|
|
|
|
|
|
|
|
||||
1|1R |
1|1L |
1| |
R |
|
| |
R |
|
|
|
|
|
*|*R |
|
|
1| |
R |
|
||||||
*|*L |
|
|
|
||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
q0 |
|bL |
q |
| |
R |
q2 |
*| |
R |
q |
|
b| R |
q |
|
|
|
|
|
9 |
|
|||||
|
|
1 |
|
|
|
|
|
|
|
10 |
|
Рисунок 3.3 - Машина Тюринга для умножения чисел
Для понимания алгоритма (рис. 3.3) существенно, что взятую в состоянии q4 единицу мы заменяем на символ e, переносим в правую сторону к краю в состоянии q5 и заменяем на единицу первый по правую сторону пустой символ; в состоянии q6 возвращает к разделителю b, а потом в состоянии q4 – к первой неперенесенной единице. В состоянии q7 множимое восстанавливается, и в состоянии q8 мы перемещаемся в левую сторону к краю для отнимания очередной единицы множителя.
Рекомендуем выполнить ручное прокручивание построенной машины для понимания ее работы.
Машину Тюринга можно в определенном смысле рассматривать как предшественник компьютера. При построении сложных машин Тюринга используют приемы, обычные для технологии программирования: последовательное соединение, ветвление, организация циклов. Следует отметить, что, хотя множество команд машины Тюринга довольно ограниченно сравнительно с современными процессорами, лента машины бесконечная, что определяет ее абстрактный, гипотетический характер. Это делает ее несравненно более мощной даже относительно суперкомпьютеров, ресурсы которых хотя и большие, но всегда конечные. Система команд компьютера формируется, как правило, исходя из критериев удобства составления программ. Система команд машины Тюринга минимальная и предназначена для выполнения формальных доказательств существования алгоритмов.
35

Следует отметить, что сеть Петри со специальными ингибиторными дугами, также как и машина Тюринга, является универсальной алгоритмической системой. Ингибиторная дуга позволяет проверить маркировку позиции на нуль. Переход срабатывает, если входная позиция не содержит маркеров. Эквивалентными машине Тюринга являются также синхронные сети Петри и сети Петри с приоритетами.
Благодаря успешному построению машин Тюринга для решения разнообразных задач была сформулирована гипотеза, названная тезисом Чорча: любой алгоритм может быть реализован с помощью соответствующей машины Тюринга. Заметим, что сначала тезис было сформулирован для рекурсивных функций Клини, но, как мы уже упоминали раньше, различные модели, предложенные для формализации интуитивного понятия алгоритма, оказались эквивалентными. Следует отметить, что тезис Чорча невозможно доказать математически, поскольку класс задач, представленный интуитивным понятием алгоритма, не определен формально. Можно было бы его опровергнуть, если бы удалось построить такой алгоритм, для реализации которого не существует машины Тюринга. Но этого никому не удалось сделать и даже, более того, построение множества машин Тюринга для решения различных задач свидетельствует о правильности тезиса. Можно привести определенную аналогию с известным в физике законом сохранения энергии, который также невозможно доказать, но и до сих пор никому не удалось его опровергнуть.
3.3 Алгоритмически неразрешимые проблемы
Создание машин Тюринга было необходимым, по существу, лишь для того, чтобы доказать, что для определенных задач не существует алгоритмов их решения. Рассмотрение таких задач начнем с воображаемой, и в некотором смысле искусственной проблемы самоприменимости машины Тюринга. Однако эта проблема будет использована нами для доказательства алгоритмической неразрешимости других задач и построения общего метода доказательства алгоритмической неразрешимости.
Закодируем программу машины Тюринга. Для этого представим функцию переходов как последовательность команд вида (q, x, q , x , r) . Занумеруем символы алфавита ленты, состояния и перемещения головки. Для разделения компонентов команды будем использовать символ *, для разделения команд - точку с запятой. Тогда программу произвольной машины Тюринга можно представить на ленте в форме:
… |
|
q |
* |
x |
* |
q` |
* |
x` |
* |
r |
; |
… |
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36

Также будем считать, что первая команда соответствует начальному состоянию машины, а последняя - заключительному.
Шифр Ш(М) машины М запишем на ленту, и ленту подадим на обработку машине М. Машина является самоприменимой, если она считывает свой шифр и через конечное количество шагов останавливается. Если машина никогда не останавливается, она является несамоприменимой. Задача состоит в том, чтобы по заданной машине M определить, является ли она самоприменимой. Для определенности будем считать, что машина MС решает задачу самоприменимости, если эта машина, считывая Ш(М), выдает на ленте 1, если М самоприменимая, и 0 – в противном случае.
Теорема 3.1. Проблема самоприменимости машины Тюринга является алгоритмически неразрешимой, т.е. не существует такой машины Тюринга МС, которая решает эту проблему.
Доказательство. Построим доказательство от противного. Предположим, что существует машина Тюринга МС, которая решает проблему самоприменимости:
МС
q0 |
q |
|
f |
Достроим МС до МП следующим образом:
|
МП |
|
|
|
|
МС |
|
1|1S |
|
|
|
|
|
|
q0 |
q |
f |
0|0S u |
f |
|
|
|
Т.е. МП, читает Ш(М) и, если М самоприменимая, попадает в q f и зацикливается;
если М несамоприменима, то МП останавливается. Тогда возникает вопрос: является ли самоприменимой МП.
Предположим, что МП самоприменимая. Тогда, считывая свой собственный шифр, МП должна остановиться. С другой стороны, машина МС считывая Ш(МП),
37

выдает 1 на ленте и попадает в q f , но тогда МП не попадает в заключительное состояние u f и не останавливается. Итак, она несамоприменима.
Пусть МП несамоприменима. Считывая свой собственный шифр Ш(МП), машина МП не останавливается. С другой стороны, МС считывая шифр Ш(МП), приходит в q f и записывает на ленте 0. Тогда МП приходит в u f и должна
остановиться.
Итак, мы имеем противоречие, поскольку предположили существование машины МС, которая решает задачу самоприменимости. Из полученного противоречия вытекает, что такой машины МС не существует.
3.4 Метод сведения
Проблема самоприменимости является первой из проблем, для которых мы доказали алгоритмическую неразрешимость. Несмотря на свой искусственный характер и удаленность от практических задач, она играет ключевую роль, поскольку будет использована в доказательстве алгоритмической неразрешимости других проблем. Метод, с помощью которого мы будем доказывать алгоритмическую неразрешимость одних проблем, используя ранее доказанную алгоритмическую неразрешимость некоторой другой проблемы, носит название метода сведения. Этот метод является основным для доказательства алгоритмической неразрешимости.
Известная история о том, как разогревают чайник инженер и математик, наглядно иллюстрирует особенности применения этого метода. Задачу первую о том, как нагреть воду, если чайник пустой, оба решают одинаково: налить воду, поставить на горелку, зажечь газ, ожидать закипание. Если же на горелке стоит теплый чайник, инженер зажигает газ и ожидает закипание. Математик же выливает воду и сводит задачу к предыдущей.
Пусть Z – определенная проблема, а {zi } – ее конкретные задачи. Например,
если Z – проблема самоприменимости, то zi заключается в |
проверке |
самоприменимости для заданной конкретной машины М, а сама Z заключается в |
|
проверке самоприменимости для произвольной машины Тюринга. |
|
Пусть имеем Z {zi } , Z {z j }.Будем говорить, что Z сводится к Z |
( Z Z ), |
если существует переход, реализованный определенным алгоритмом, от каждой zi к некоторой z j такой, что ответ для zi положительный тогда и только тогда, когда ответ для z j также положительный.
38

Если доказано, что Z алгоритмически неразрешимая, |
тогда Z также должна |
|||
быть алгоритмически неразрешимая. На |
самом |
деле, в |
том случае, если Z |
|
разрешима с помощью, например, машины |
М0, |
последовательное соединение |
||
M 1 |
M 0 |
|
|
|
машин позволяет решить проблему Z: zi |
z j |
{0,1}. |
|
|
Пусть надо доказать алгоритмическую неразрешимость Z, тогда мы стараемся найти уже доказанную алгоритмически неразрешимую проблему Z0 и, кроме этого, стараемся построить последовательность сводимых проблем: Z0 Z1 ... Z . Если это удается, то тем самым мы доказываем алгоритмическую неразрешимость проблемы Z.
Проиллюстрируем использование метода сведения на примере доказательства алгоритмической неразрешимости проблемы останова машины Тюринга.
Проблема останова машины Тюринга заключается в том, чтобы для произвольной машины Тюринга М и произвольной записи на ленте X определить, остановится ли машина М при обработке входной ленты X.
Теорема 3.2. Проблема останова машины Тюринга является алгоритмически неразрешимой.
Доказательство. Построим доказательство от противного. Пусть проблема останова разрешима. Тогда, выбрав вместо X шифр Ш(М), мы сможем решать проблему самоприменимости. Итак, мы приходим к противоречию, что и доказывает теорему.
Приведем несколько известных примеров алгоритмически неразрешимых проблем:
1. Проблема распознавания истинности формул элементарной арифметики. Формулы строятся с помощью арифметических действий (сложение и
умножение), логических операций (логических связок и кванторов) и знака равенства из константы 1 и натуральнозначних переменных. Проблема состоит в требовании найти алгоритм, который по каждой такой формуле определял бы, выполняется она на натуральном ряде или нет.
2. Проблема сочетаемости Поста.
Пусть задано конечное множество V пар слов в определенном алфавите. Назовем это множество сочетаемым, если для некоторых последовательностей пар ( A1, B1) , ( A2 , B2 ) ... ( As , Bs ) из V выполняется равенство A1...As B1...Bs . Необходимо по любому заданному конечному множеству V пар слов в указанном алфавите установить, сочетаемо оно или нет.
3. Проблема представления матриц.
39
