
- •Математические модели информационных процессов и управления
- •212030, Г. Могилев, пр. Мира, 43
- •Задание 1 Множества. Алгебра множеств.
- •Законы для объединения и пересечения:
- •Законы для дополнений:
- •Законы для разностей множеств:
- •Список использованных источников
- •Задание 2 Кортежи и операции над ними.
- •Список использованных источников
- •Задание 3 Комбинаторные формулы.
- •Список использованных источников
- •Задание 4 Логические операции. Основные законы.
- •1.1 Составные высказывания
- •1.2. Простейшие связки
- •1.3. Другие связки
- •1.4. Основные законы, определяющие свойства введенных логических операций
- •Список использованных источников
- •Задание 5 Алгебра высказываний.
- •1.1 Логические отношения
- •1.2 Варианты импликации
- •1.3 Пример вывода логического заключения
- •Список использованных источников
- •Задание 6 Булевы функции. Многочлены Жегалкина.
- •1.1 Свойства элементарных булевых функций
- •1.2 Дизъюнктивные и конъюнктивные нормальные формы алгебры высказываний
- •1.3 Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
- •1.4 Многочлены Жегалкина
- •Список использованных источников
- •Задание 7 Минимизация булевых функций.
- •1.1 Метод карт Карно
- •1.2 Метод Петрика
- •Список использованных источников
- •Задание 8 Логика предикатов.
- •1.1 Предикаты
- •1.2. Применение предикатов в алгебре
- •1.3. Булева алгебра предикатов
- •1.4. Кванторы
- •1.5. Формулы логики предикатов
- •Список использованных источников
- •Задание 9 Приведение формул логики предикатов к сколемовской нормальной форме.
- •1.2 Приведенные и нормальные формы в логике предикатов
- •Список использованных источников
- •Задание 10 Логический вывод.
- •1.1 Исчисление предикатов
- •1.2 Автоматическое доказательство теорем.
- •Список использованных источников
- •Задание 11 Способы задания графов.
- •1.1 Аналитический способ задания графов
- •1.4. Графическое представление бинарного отношения
- •Множеств а и в
- •1.5 Части графа
- •1.8 Операции над графами
- •Список использованных источников
- •Задание 12 Решение задач оптимизации на графах.
- •1.1 Алгоритм поиска кратчайшего пути
- •1.2. Алгоритмы поиска всех кратчайших путей
- •1.3 Алгоритм нахождения максимального потока на сети (алгоритм Форда -Фалкерсона)
- •1)Построим начальный поток.
- •Список использованных источников
Список использованных источников
1 Майника, Э. Алгоритмы оптимизации на сетях и графах : пер. с англ. / Э. Майника. - М.: Мир, 1981. − 323 с.
2 Сборник задач и упражнений по высшей математике: Математическое программирование: Учеб. пособие/ А.В.Кузнецов, В.А.Сакович, Н.И.Холод и др.; Под общ. ред. А.В.Кузнецова. – Мн.: Выш. шк., 1995. – 382с.: ил.
Приложение А
Бланки вариантов практического задания для самостоятельной работы
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 01
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Следующий опрос 100 студентов выявил следующие данные о числе студентов, изучающих различные иностранные языки: только немецкий – 18; немецкий, но не испанский – 23; немецкий и французский – 8; немецкий – 26; французский – 48; французский и испанский – 8; никакого языка – 24.
а) Сколько студентов изучают испанский язык?
б) Сколько студентов изучают немецкий и испанский языки?
в) Сколько студентов изучают французский язык, в том и только в том случае, если они не изучают испанский?
Задание 2. Сравните кортежи <|−3|, |−5|, −8> и <3, 5, |−8|>.
Задание 3. Сколькими способами могут восемь человек стать в очередь к театральной кассе?
Задание
4. Определить
двумя способами: 1) методом таблиц
истинности и 2) методом редукции, являются
ли формулы тавтологиями: 1)
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Устрицы молчаливы. Молчаливые существа не очень-то забавны. Я не люблю не забавных существ.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]() .
.
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
xy(P(x)Q(y)R).
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Области определения: множество людей и множество книг. Все студенты читают учебники. Некоторые студенты не читают стихов. Следовательно, ни один учебник не написан в стихах.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
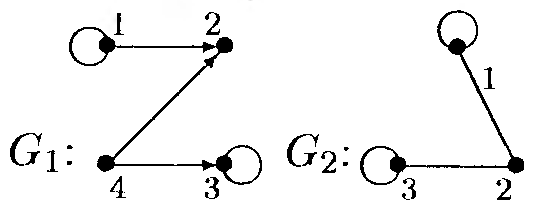
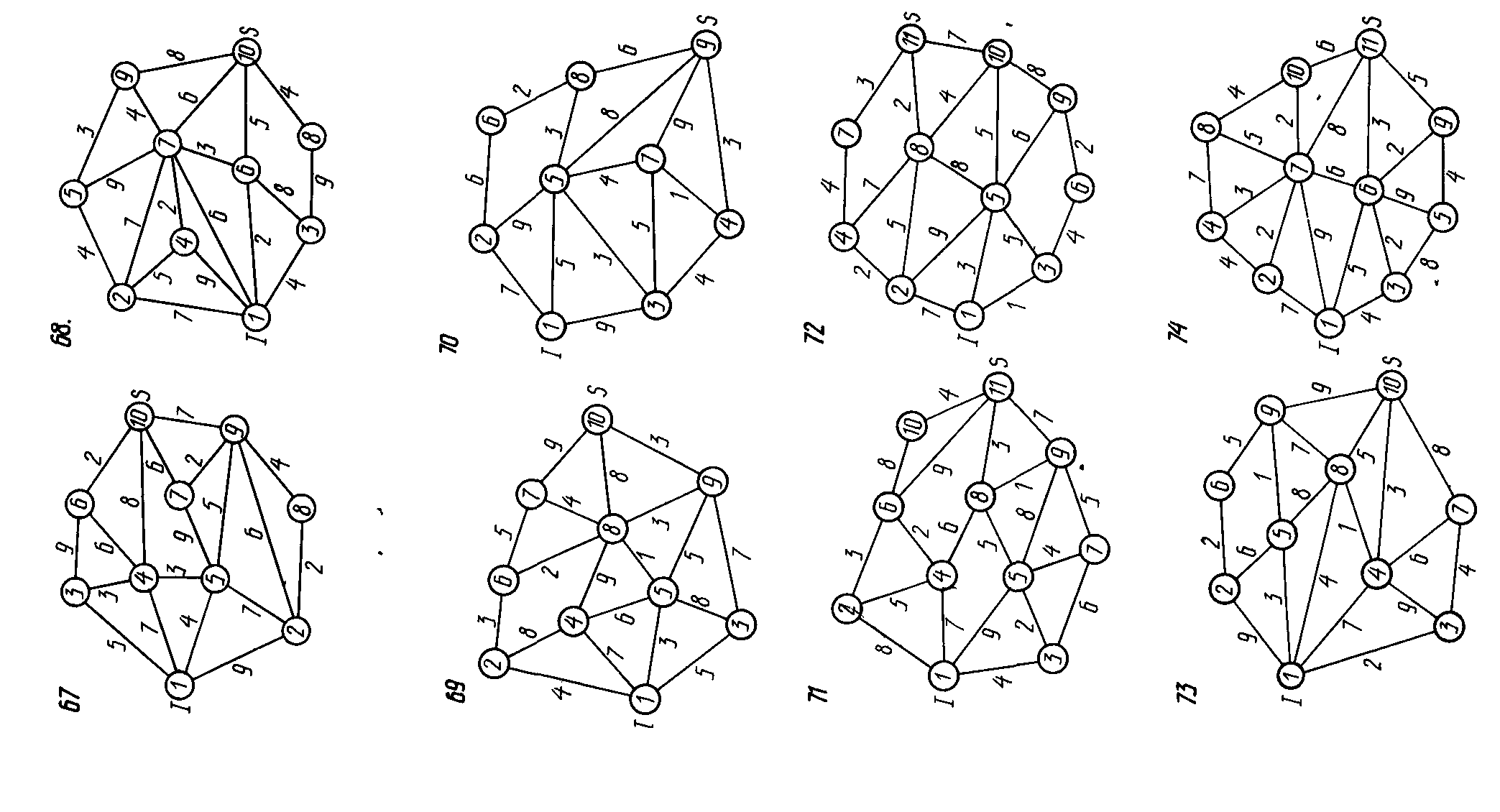
Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 02
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. В отчете об опросе 100 студентов (см. задачу 4 в п. 2) сообщалось, что количество студентов, изучающих различные языки, таково: все три языка – 5; немецкий и испанский – 10; французский и испанский – 8; немецкий и французский – 20; испанский – 30; немецкий – 23; французский – 50. Инспектор, представивший этот отчет, был уволен. Почему?
Задание 2. Сравните кортежи <cos(π), cos(π/2), cos(0)>, <1, −1, 0>.
Задание 3. В автомашине 7 мест. Сколькими способами семь человек могут усесться в эту машину, если занять место водителя могут только трое из них?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Устрицы молчаливы. Молчаливые существа не очень-то забавны. Я не люблю не забавных существ.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(Ry(P(x) Q(y)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: люди. Ни один торговец подержанными автомобилями не покупает подержанные автомобили для своей семьи. Некоторые люди, которые покупают подержанные автомобили для своих семей, абсолютно нечестны. Следовательно, некоторые абсолютно нечестные люди не являются торговцами подержанными автомобилями.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
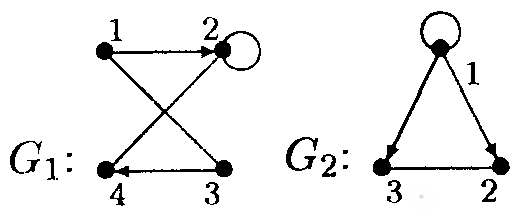
Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 03
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Воспользовавшись диаграммой Эйлера-Венна, определите, какие из следующих высказываний логически истинны:
а)
![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() д)
д) ![]()
Задание 2. Сравните кортежи <2, 2, 5> и <2, 2, 5, 5>.
Задание 3. В автомашине 5 мест. Сколькими способами 5 человек могут усесться в эту машину, если занять место водителя могут только трое из них?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Разумные люди ходят на ногах. Неразумные люди ходят на руках.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(Ry(P(x) Q(y)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: люди. Каждый, кто идет в кино, покупает билет. Следовательно, если не существует билетов, то никто не ходит в кино.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 04
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Найдите множества истинности каждого высказывания и, воспользовавшись диаграммой Эйлера-Венна, определите, какие из выписанных ниже пар высказываний состоят из высказываний, одно из которых является следствием другого:
![]()
Задание 2. Сравните кортежи <cos(π), cos(π/2), cos(0)>, <−1, 0, 1>.
Задание 3. Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трех цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Музыка, которую слышно, вызывает колебания воздуха. Музыка, которую не слышно, не стоит того, чтобы за нее платили деньги.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(Ry(Q(y)P(x)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: люди. Ни один лентяй не достоин славы. Некоторые художники не лентяи. Следовательно, некоторые художники достойны славы.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 05
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Для следующих трех составных высказываний:
а) введите буквенные обозначения для компонент;
б) дайте символическое выражение;
в) найдите множества истинности;
г) проверьте их совместимость.
Если этот курс интересен, то я буду упорно над ним работать. Если этот курс не интересен, то я получу по нему плохую отметку. Я не буду упорно работать, но получу по этому курсу хорошую отметку.
Задание 2. Сравните кортежи <4, |−3|, 5> и <3, 4, 5>.
Задание 3. Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, а) если первая из них не равна нулю; б) если номер состоит из одной буквы латинского алфавита, за которой следуют четыре цифры, отличные от нуля?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если я поеду автобусом, а автобус опоздает, то я опоздаю на занятия. Если я опоздаю на занятия, то я начну огорчаться. Если я огорчен, то мне не следует ехать домой.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x) y(R Q(y)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: студенты. Некоторые первокурсники любят всех второкурсников. Ни один первокурсник не любит никого из студентов предпоследнего курса. Следовательно, ни один второкурсник не является студентом предпоследнего курса.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 06
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Каждому множеству поставьте в соответствие высказывание, имеющее это множество своим множеством истинности, и, воспользовавшись таблицами истинности, определите, какие из следующих множеств пусты:
![]()
Задание
2. Задать
бинарное отношение на множестве
натуральных чисел N = {1,
2, 3, 4, 5, 6, 7, 8} R
= "быть не больше
![]() ".
".
Задание 3. Сколькими способами можно расставить на полке семь книг, если (а) две определенные книги должны всегда стоять рядом, (б) эти две книги не должны стоять рядом?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если Смит победит на выборах, он будет доволен, а если он будет доволен, то он плохой борец в предвыборной кампании. Но если он провалится на выборах, то потеряет доверие партии. Если он плохой борец в предвыборной кампании, ему следует выйти из партии. Смит или победит в предвыборной кампании, или провалится. Он плохой борец, если потеряет доверие партии.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x) y(Q(y) P(x)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: животные. 1. Я люблю всех животных, которые принадлежат мне. 2. Собаки грызут кости. 3. Ни одно животное я не пускаю к себе в кабинет, если оно не «служит», когда его об этом просят. 4. Все животные во дворе принадлежат мне. 5. Всем животным, которых я люблю, разрешается входить ко мне в кабинет. 6. Единственные животные, которые «служат», если их попросить, – собаки. Следовательно, все животные в этом дворе грызут кости.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 07
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Каждому множеству поставьте в соответствие высказывание, имеющее это множество своим множеством истинности, и, воспользовавшись таблицами истинности, определите, являются ли попарно различными следующие множества:
![]()
![]()
Задание 2. Задать бинарное отношение на множестве натуральных чисел N = {1, 2, 3, 4, 5, 6, 7, 8} R = "быть делителем".
Задание 3. Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если Петров член нашей команды, то он обязательно храбрый и хорошо владеет техникой удара. Но он не входит в состав нашей команды.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x)&y(Q(y) R))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: дни. 1. Я не называю день «несчастливым», если Робинсон вежлив со мной. 2. Среды всегда бывают пасмурными днями. 3. Если люди берут с собой зонты, день никогда не бывает солнечным. 4. Единственный день недели, когда Робинсон невежлив со мной, – среда. 5. Всякий возьмет с собой зонт, если идет дождь. 6. Мои «счастливые» дни неизменно оказываются солнечными. Следовательно, дождливые дни пасмурны.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 08
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Каждому множеству поставьте в соответствие высказывание, имеющее это множество своим множеством истинности, и, воспользовавшись таблицами истинности, определите, в каких из следующих пар множеств одно из множеств является подмножеством другого:
![]()
Задание 2. Задать бинарное отношение на множестве натуральных чисел N = {1, 2, 3, 4, 5, 6, 7, 8} R = "быть равным".
Задание 3. Компания из двадцати мужчин разделяется на три группы, в первую из которых входят три человека, во вторую − пять и в третью − двенадцать. Сколькими способами они могут это сделать? (Ответ записать в виде произведения сомножителей, не вычисляя его.).
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Зарплата возрастает только, если будет инфляция. Если будет инфляция, то увеличится стоимость жизни. Если стоимость жизни возрастает, то люди несчастны.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x) y(Q(y) R) S)
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: люди. 1. Никто не забудет причесаться, если он отправляется на бал. 2. Нельзя сказать, что человек выглядит превосходно, если он неопрятен. 3. Курильщики опиума утрачивают контроль над собой. 4. Причесанный человек выглядит превосходно. 5. Никто не наденет белых лайковых перчаток, если он не отправляется на бал. 6. Человек всегда неопрятен, если он утратил контроль над собой. Следовательно, курильщики опиума никогда не носят белых лайковых перчаток.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 09
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание
1. Докажите,
как с помощью таблиц истинности, так и
с помощью диаграммы Эйлера-Венна, что
высказывание ![]() эквивалентно высказыванию
эквивалентно высказыванию ![]() .
.
Задание 2. Задать бинарное отношение на системе множеств 2М, М = {1, 2, 3} R = "пересекаться с" (иметь непустое пересечение).
Задание 3. Сколько четырехбуквенных слов можно образовать из букв слова сапфир? Сколько среди них таких, которые не содержат буквы р? Сколько таких, которые начинаются с буквы с и оканчиваются буквой р?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если конгресс отказывается принять новые законы, то забастовка не будет окончена, кроме случая, когда она длится более года. Забастовка также будет окончена, если президент фирмы уйдет в отставку. Конгресс отказывается действовать, забастовка оканчивается, и президент фирмы не уходит.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x)& y Q(y)) x P(x)
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: представленные здесь картины. 1. Ни одна из представленных здесь картин, кроме батальных, не представляет ценности. 2. Ни одна из картин, вывешенных без рам, не покрыта лаком. 3. Все батальные картины написаны маслом. 4. Все распроданные картины представляют ценность. 5. Все картины английских мастеров покрыты лаком. 6. Все картины, которые были вывешены в рамах, проданы. Следовательно, все представленные здесь картины английских мастеров написаны маслом.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:
доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 10
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Проверьте все законы операций над множествами для объединения и пересечения с помощью диаграмм Эйлера-Венна. Переведите эти законы в законы для составных высказываний. Проверьте их с помощью таблиц истинности.
Задание 2. Равны ли следующие кортежи: <a, {a, b, c}, b, c> и <a, {a, b, c}, {b, c}>?
Задание 3. Найдите четвертый член разложения (a+3)7.
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если человек стремится постичь смысл жизни, то он умеет вышивать крестиком. Боксеры не умеют вышивать крестиком.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
xy(P(x) Q(y) Q(y))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: мои мысли. 1. Любая мысль, которую нельзя выразить в виде силлогизма, поистине смешна. 2. Моя мечта о сдобных булочках не стоит того, чтобы ее записывать на бумаге. 3. Ни одну мою несбыточную мечту нельзя выразить в виде силлогизма. 4. Мне не приходило в голову ни одной действительно смешной мысли, о которой бы я не сообщил своему поверенному. 5. Я только и мечтаю, что о сдобных булочках. 6. Я никогда не высказывал своему поверенному ни одной мысли, если она не стоила того, чтобы ее записать на бумагу. Следовательно, все мои мечты сбылись.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 11
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Проверьте все законы операций над множествами для дополнений и для разностей с помощью диаграмм Эйлера-Венна, переведите их в законы для составных высказываний и проверьте их с помощью таблиц истинности.
Задание 2. Равны ли следующие кортежи: <a, {a, b, c}, b, c> и < a, {a, b, c}, b, c >?
Задание
3. Найдите
четвертый член разложения ![]() .
.
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
В день дождливый Боб не ходит на прогулку. Без свежего воздуха у него пропадает аппетит.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x)& y(Q(y) P(x)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: предметы. 1. Я с отвращением отношусь ко всему, что не может служить мостом. 2. Все, что можно воспеть в стихах, для меня приятный подарок. 3. Радуга не выдержит веса тачки. 4. Все, что может служить мостом, выдержит вес тачки. 5. Я не принял бы в качестве подарка то, что вызывает у меня отвращение. Следовательно, радугу не стоит воспевать в стихах.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 12
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Из законов булевой алгебры над множествами получите следующие результаты:
![]()
![]()
Задание 2. Равны ли следующие кортежи: <a, {a, b, c}, b, c> и < a, {a, b, c}, c, b>?
Задание 3. Найдите восьмой член разложения (a2+b3)13.
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Рыбак ловит рыбу. Тот, кто ловит рыбу – оптимист. Оптимист не предается отчаянию.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(y(P(x) R(y))Q)
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: авторы литературных произведений. 1. Все авторы литературных произведений, постигшие природу человека, умные люди. 2. Ни одного автора нельзя считать истинным поэтом, если он не способен волновать сердца людей. 3. Шекспир написал «Гамлета». 4. Ни один автор, не постигший природу человека, не способен волновать сердца людей. 5. Только истинный поэт мог написать «Гамлета». Вывод: Шекспир был умным человеком.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 13
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике, астрономии. Три спецкурса посещают 10 студентов, по математике и физике − 30, по математике и астрономии − 25; спецкурс только по физике − 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике − 145, по астрономии − 100 студентов. Сколько студентов посещают спецкурс только по астрономии? Сколько студентов посещают два спецкурса?
Задание 2. Равны ли следующие кортежи: <a, {a, b, c}, b, c> и < a, {a, b, c}, a, b, c> ?
Задание
3. Найдите
средний член разложения ![]() .
.
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
В хорошую погоду кошка ходит гулять. Если кошка больна, то она сидит дома.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x)& z R(z) y Q(y))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: люди этого колледжа. 1. Все выпускники Итона в этом колледже играют в крикет. 2. Никто, кроме преподавателей, не обедает за верхним столом. 3. Ни один из тех, кто играет в крикет, не умеет грести. 4. Все мои друзья в этом колледже – выпускники Итона. 5. Все преподаватели – прекрасные гребцы. Вывод: все мои друзья обедают за нижним столом.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

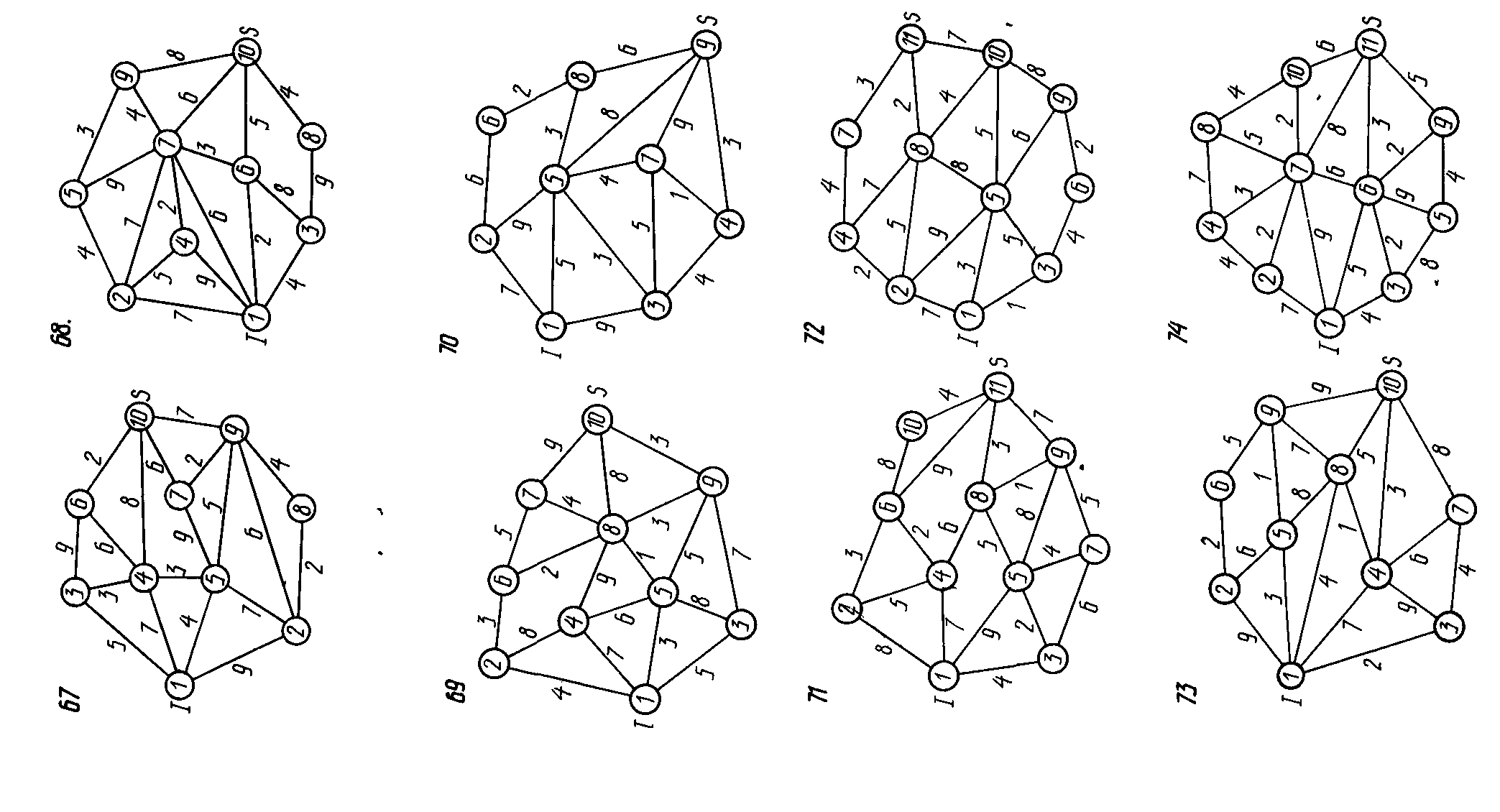
Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:
доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 14
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. 500 студентов посещают три спецкурса. Спецкурс только по математике, только по математике и физике и только по физике и астрономии посещают одинаковое число студентов; три спецкурса посещают 20 студентов. Спецкурс по математике посещают столько же студентов, сколько спецкурс по физике. Один спецкурс по физике посещают 50 студентов, а спецкурс по астрономии − 250 студентов. Сколько студентов посещают только один спецкурс?
Задание
2. Пусть A={1,
2, 3}, B={x,
y}.
Выписать все элементы декартова
произведения ![]() .
.
Задание
3. Найдите
средний член разложения ![]() .
.
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Деревья, которые растут в этом саду, плодоносят. Деревья, которые плодоносят, дают хороший урожай. Деревья, дающие хороший урожай, получают тщательный уход. Ни одно дерево в этом саду не получает тщательного ухода.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x((P(x)y Q(y))&P(x))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: люди. 1. Те, кто нарушает свои обещания, не заслуживают доверия. 2. Любители выпить очень общительны. 3. Человек, выполняющий свои обещания, честен. 4. Ни один трезвенник не ростовщик. 5. Тому, кто очень общителен, всегда можно верить. Вывод: ни один ростовщик не бывает нечестен.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 15
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Экзамен по математике содержал три задачи: по алгебре, по геометрии и по тригонометрии. Из 750 абитуриентов задачу по алгебре решили 400 абитуриентов, по геометрии − 480, по тригонометрии − 420; задачи по алгебре или геометрии решили 630 абитуриентов; по геометрии или тригонометрии − 600 абитуриентов; по алгебре или тригонометрии − 620 абитуриентов; 100 абитуриентов не решили ни одной задачи. Сколько абитуриентов решили все задачи? Сколько абитуриентов решили только одну задачу?
Задание
2. Из цифр 1,
2, 3, 4, 5 составьте все двузначные числа.
Как связано получившееся множество с
декартовым произведением ![]() ,
где А={1, 2, 3, 4, 5}?
,
где А={1, 2, 3, 4, 5}?
Задание
3. Найдите
два средних члена разложения ![]() .
.
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если человек достоин славы, то он получает награду. Если человек не храбрый, то он не достоин славы.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
y(P(y) xQ(x) P(y))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: плоды на этой выставке. 1. Все плоды на этой выставке, которые не будут удостоены награды, являются собственностью организационного комитета. 2. Ни один из представленных мной персиков не удостоен награды. 3. Ни один из плодов, распроданных после закрытия выставки, не был незрелым. 4. Ни один из спелых плодов не был выращен в теплице. 5. Все плоды, принадлежащие оргкомитету выставки, были распроданы после ее закрытия. Вывод: ни один из моих персиков не был выращен в теплице.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 16
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Экзамен по математике содержал три задачи: по алгебре, геометрии и тригонометрии. Из 800 абитуриентов задачу по алгебре решили 250 человек, по алгебре или геометрии − 660 человек, по две задачи решили 400 человек, из них две задачи по алгебре и геометрии решили 150 человек, по алгебре и тригонометрии 50 человек; ни один абитуриент не решил все задачи; 20 абитуриентов не решили ни одной задачи; только по тригонометрии задачи решили 120 человек. Сколько решили только одну задачу? Сколько человек решили задачи по геометрии?
Задание
2. Рассмотрим
два множества A={a,
b,
c,
d,
e,
f,
g,
h}
и B={1,
2, 3, 4, 5, 6, 7, 8}. Составьте множество пар
![]() .
Что это множество представляет?
.
Что это множество представляет?
Задание 3. Определите х из условия, что третий член разложения бинома (x+xlgx)5 равен 1000000.
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если идет дождь, то это наводит скуку. Осенью идет дождь.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
y(P(y) x R(x))Q
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: поэмы. 1. Ни одна интересная поэма не останется непризнанной людьми с тонким вкусом. 2. Ни одна современная поэма не свободна от аффектации. 3. Все ваши поэмы написаны о мыльных пузырях. 4. Ни одна аффектированная поэма не находит признания у людей с тонким вкусом. 5. Ни одна древняя поэма не написана о мыльных пузырях. Вывод: все ваши поэмы не интересны.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 17
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. На кафедре иностранных языков работают 18 преподавателей, из них 12 преподают английский язык, 11 – немецкий, 9 − французский; 5 преподавателей преподают английский и немецкий языки, 4 − английский и французский, 3 – немецкий и французский. Сколько преподавателей преподают все три языка? Только два языка?
Задание
2. Если А={2,
3, 4, 5, 6, 7, 8}, запишите бинарное отношение
![]() ,
x
делит y,
и x≤3}.
,
x
делит y,
и x≤3}.
Задание 3. Найдите тот член разложения бинома
![]() ,
,
который после упрощения содержит z5, если сумма биномиальных коэффициентов этого разложения равна 128.
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Лекарства противны на вкус. Настои из трав – это лекарства.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
xy(P(x) Q(y)) R
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: книги в этой библиотеке. 1. Единственные книги в этой библиотеке, которые я не рекомендую читать, безнравственны по своему содержанию. 2. Все книги в твердых переплетах обладают выдающимися литературными достоинствами. 3. Все романы вполне нравственны по своему содержанию. 4. Я не рекомендую вам читать ни одну из книг в мягкой обложке. Вывод: все романы в этой библиотеке обладают выдающимися литературными достоинствами.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
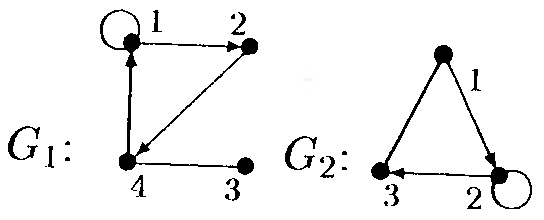
Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 18
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. На кафедре иностранных языков работают 37 преподавателей, из них французский преподают 23 преподавателя, английский язык 28 преподавателей, все три языка − три преподавателя. Число преподавателей, ведущих занятия только по английскому языку равно числу преподавателей, ведущих занятия только по немецкому языку. Число преподавателей, ведущих занятия только по английскому и немецкому языкам, равно числу преподавателей, ведущих занятия только по немецкому и французскому языкам. Сколько преподавателей преподают один иностранный язык? Сколько преподавателей преподают один английский язык?
Задание
2. Если А = {2,
3, 5, 7, 9, 11, 12}, В= {−5, −4, −3, −2, −1, 3, 4, 8}
запишите бинарное отношение R = {<x,y>:
x![]() A,
y
A,
y![]() B,
х делится на 3, |y|
B,
х делится на 3, |y|![]() 4}.
4}.
Задание 3. Сколько различных коллекций из десяти монет можно собрать из монет стоимостью 1 цент, 5 центов, 10 центов, 25 центов и 50 центов?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Битвы сопровождаются страшным шумом. Если что-то происходит без шума, то оно может ускользнуть от нашего внимания.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x P(x) y Q(y) R
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: вещи. 1. Все вещи, продаваемые на улице, не имеют особой ценности. 2. Только дрянь можно купить за грош. 3. Яйца большой гагарки представляют большую ценность. 4. Лишь то, что продается на улице, и есть настоящая дрянь. Вывод: яйцо большой гагарки за грош не купишь.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 19
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. На курсах иностранных языков учится 600 человек, из них французский изучают 220 человек, английский − 270 человек, слушатели, изучающие английский язык, не изучают немецкий язык; один французский язык изучают 100 человек, один немецкий − 180 человек. Сколько человек изучает по два иностранных языка? Сколько человек изучает один иностранный язык?
Задание
2. Если А = {2,
3, 5, 7, 9, 11, 12}, В= {−5, −4, −3, −2, −1, 3, 4, 8}
запишите бинарное отношение R = {<x,y>:
x![]() A,
y
A,
y![]() B,
х делится на 3, |y|
B,
х делится на 3, |y|![]() x}.
x}.
Задание 3. В киоске продается мороженое 21 вида. Фрэд хочет купить пять порций мороженого. Если мороженого одного вида может быть более одной порции, то сколько существует способов сделать покупку?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Рыбы умеют плавать. Если это морская звезда, то она тоже – рыба.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x) y Q(y) R)
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: мои дети. 1. Все мои сыновья стройны. 2. Никто из моих детей не здоров, если он не делает утренней зарядки. 3. Все обжоры среди моих детей страдают ожирением. 4. Ни одна из моих дочерей не делает утренней зарядки. Вывод: все мои дети-обжоры не здоровы.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 20
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Группа студентов из 25 человек сдала экзаменационную сессию следующими результатами: 2 человека получили только “отлично”, 3 человека получили отличные, хорошие и удовлетворительные оценки; 4 человека только “хорошо”; 3 человека только хорошие и удовлетворительные оценки; число студентов, сдавших сессию только на “отлично”, “хорошо”, равно числу студентов, сдавших сессию только на “удовлетворительно”. Студентов, получивших только отличные и удовлетворительные оценки − нет. Удовлетворительные или хорошие оценки получили 22 студента? Сколько студентов не явилось на экзамены? Сколько студентов сдали сессию только на “удовлетворительно”?
Задание
2. Если А = {2,
3, 5, 7, 9, 11, 12}, В= {−5, −4, −3, −2, −1, 3, 4, 8}
запишите бинарное отношение R = {<x,y>:
x![]() A,
y
A,
y![]() B,
х делится на 2, |y|
B,
х делится на 2, |y|![]() x}.
x}.
Задание 3. Если в урне имеются 20 красных, 20 зеленых и 20 синих шаров, то сколькими различными способами можно выбрать 10 шаров?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Книги с острым сюжетом не подходят для чтения легко возбудимым людям. От книг со спокойным сюжетом клонит в сон.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(y(RP(x) Q(y)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: люди. 1. Ни один ребенок не обладает терпением. 2. Ни один нетерпеливый человек не может сидеть спокойно. Вывод: любой ребенок не усидит на месте.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 21
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. На курсы иностранных языков зачислено 300 слушателей. Из них французский или английский изучают 250 человек, английский и немецкий − 60 человек, английский и французский − 80 человек; число слушателей, изучающих только французский язык, равно числу слушателей, изучающих только немецкий язык; 70 человек изучает только английский язык. Занятия по французскому и немецкому языкам проводятся единовременно. Сколько слушателей изучает немецкий язык или французский? Сколько слушателей не посещает занятия?
Задание
2. Если А = {2,
3, 5, 7, 9, 11, 12}, В= {−5, −4, −3, −2, −1, 3, 4, 8}
запишите бинарное отношение R = {<x,y>:
x![]() A,
y
A,
y![]() B,
х делится на 3, |y|
делится на 2}.
B,
х делится на 3, |y|
делится на 2}.
Задание 3. Цветочник продает 10 видов цветов. Сколько различных букетов из 12 цветков он может сделать?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если я читал статью, то она была напечатана в газете. Если что-то напечатано в газете, то это может быть небылицей.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x) y(Q(y) P(x)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: люди. 1. Ни одна из моих кузин не справедлива. 2. Все судьи справедливы. Вывод: среди моих кузин нет судей.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 22
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Преподаватели кафедры Прикладной математики преподают на трех факультетах: механическом, технологическом, экономическом. На технологическом факультете работает 22 преподавателя, на механическом − 23 преподавателя, на механическом и экономическом − 36 преподавателей; только на технологическом факультете − 10 преподавателей; 2 − на трех факультетах; 5 преподавателей работают только на механическом и экономическом факультетах. Число преподавателей, работающих только на механическом и технологическом факультетах, равно числу преподавателей, работающих на экономическом и технологическом факультетах. Сколько преподавателей работает на кафедре? Сколько преподавателей работают только на одном факультете?
Задание 2. Записать бинарное отношение на множестве людей (рис. 1) R = "быть сыном".

Рисунок 1.
Задание 3. Сколько существует чисел, меньших 10000 и таких, что сумма цифр равна 12?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если человек не обладает чувством юмора, то он скучен. Скучных людей не приглашают в компании. Если человека не приглашают в компании, то его жизнь становится невыносимой.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
y(x P(x) Q(y) Q(y))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Область определения: живые существа. 1. Ни одно толстое создание не бегает хорошо. 2. Некоторые гончие бегают хорошо. Вывод: гончих трудно назвать толстыми.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 23
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике, астрономии. Три спецкурса посещают 10 студентов, по математике и физике − 30, по математике и астрономии − 25; спецкурс только по физике − 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике − 145, по астрономии − 100 студентов. Сколько студентов посещают спецкурс только по астрономии? Сколько студентов посещают два спецкурса?
Задание 2. Записать бинарное отношение на множестве людей (рис. 1) R = "быть братом".

Рисунок 1.
Задание 3. Человек покупает 12 различных игрушек для своих четырех детей. Сколькими способами он может распределить игрушки? А сколькими способами, если игрушки делить поровну?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Мука пригодна для пищи. То, что пригодно для пищи, продается в продуктовых магазинах.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(P(x)& y(Q(y) P(x)))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Области определения: множество людей и множество книг. 1. Некоторые люди пишут стихи. 2. Те, кто пишет стихи – поэты. 3. Все поэты любят читать стихи. Вывод: некоторые люди любят читать стихи.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:
доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 24
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. 500 студентов посещают три спецкурса. Спецкурс только по математике, только по математике и физике и только по физике и астрономии посещают одинаковое число студентов; три спецкурса посещают 20 студентов. Спецкурс по математике посещают столько же студентов, сколько спецкурс по физике. Один спецкурс по физике посещают 50 студентов, а спецкурс по астрономии − 250 студентов. Сколько студентов посещают только один спецкурс?
Задание 2. Записать бинарное отношение на множестве элементов структуры (рис. 1) R = "быть непосредственно связанным с".

Рисунок 1.
Задание 3. Сколько различных перестановок можно образовать изо всех букв слова перестановка? Сколько из них начинается с буквы п и оканчивается буквой а?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если человек добился успеха, то он прилежен. Прилежные люди счастливы.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x(y(P(x) (RQ(y))))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Области определения: множество людей и множество литературных произведений. 1. Некоторые студенты читают стихи. 2. Ни один студент не читает шпаргалки. Вывод: ни одна шпаргалка не рифмована.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
В А Р И А Н Т № 25
по курсу «МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И УПРАВЛЕНИЯ»
Студент ______________________________
Номер зачетной книжки_________________
Задание 1. Экзамен по математике содержал три задачи: по алгебре, по геометрии и по тригонометрии. Из 750 абитуриентов задачу по алгебре решили 400 абитуриентов, по геометрии − 480, по тригонометрии − 420; задачи по алгебре или геометрии решили 630 абитуриентов; по геометрии или тригонометрии − 600 абитуриентов; по алгебре или тригонометрии − 620 абитуриентов; 100 абитуриентов не решили ни одной задачи. Сколько абитуриентов решили все задачи? Сколько абитуриентов решили только одну задачу?
Задание 2. Записать бинарное отношение на множестве элементов структуры (рис. 1) R = "быть начальником".

Рисунок 1.
Задание 3. Сколько пятибуквенных слов, каждое из которых состоит из трех согласных и двух гласных, можно образовать из букв слова уравнение?
Задание 4. Определить двумя способами: 1) методом таблиц истинности и 2) методом редукции, является ли формула тавтологией:
![]()
Задание 5. Вывести (если возможно) заключение из набора посылок:
Если студент прогуляет много занятий, то он получит двойку на экзамене. Если он получит двойку на экзамене, то пропадут каникулы. Студент может хорошо отдохнуть, если у него будут каникулы.
Задание 6. Постройте таблицу истинности функции. С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ. Составьте двумя способами полином Жегалкина и проверьте линейность функции:
![]()
Задание 7. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции:
![]()
Задание 8. Построить таблицы истинности на области интерпретации D={1,2}:
x((P(x) y Q(y))&P(x))
Задание 9. Проверить логическую общезначимость и получить нормальную форму следующей формулы:
![]()
Задание 10. Проверить логическое следование: Области определения: множество людей и множество литературных произведений. 1. Некоторые студенты пишут некоторые учебники. 2. Все студенты пишут только письма. Вывод: некоторые учебники можно отнести к эпистолярному жанру.
Задание
11. Даны графы![]() и
и![]() .
Найдите
.
Найдите![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),![]()
![]()
![]() ,
,![]() +
+![]() .
Для графа
.
Для графа![]()
![]()
![]() найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.
найдите матрицы смежности, инцидентности,
сильных компонент, маршрутов длины 2 и
все маршруты длины 2, исходящие из вершины
1.

Задание 12. На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы. Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности:

доцент каф. АСУ, к.т.н. ________________ А.И.Якимов
Задание принял к исполнению:
« ___ » ___________ 201_ г. __________(подпись студента)
