Теоретическая механика2

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусско-Российский университет

Предмет:

Теоретическая механика

Файл:

– момент инерции блока 2 относительно оси его вращения

.pdf

Скачиваний:

Добавлен:

29.02.2016

Размер:

724.38 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

При t = τ , когда камень находится в точке B , покидая участок AB , имеем

vB = g (sin α − f cosα) τ + vA ;

l =	g (sin α − f cosα)	τ2	+ vA τ .

2

После подстановки известных численных данных получим, что vB = 9,8 (sin 30 − 0,1 cos30) τ + vA ;

0,7 =	9,8 (sin 30 − 0,1 cos30)	τ2	+ vA τ .
В итоге	2
В итоге	vB = 4,051 τ + vA ;
	vB = 4,051 τ + vA ;
	0,7 = 2,026 τ2 + vA τ .		(4)

Рассмотрим теперь движение камня на участке BC . Дифференциальные уравнения движения камня на данном участке:

m x = ∑ Fix ;

	m y = ∑ Fiy .		(5)
На участке BC на камень действует лишь сила тяжести G , поэтому
уравнения (5) примут следующий вид:
		m x = 0 ;
	m y = m g .
В итоге
		x = 0 ;
		y = g .
После двойного интегрирования получим
		x = C3 ;
	y = g t + C4 ;
x = C3 t + C5 ;
y =	g	t 2 + C4 t + C6 .	(6)

2
Постоянные интегрирования находим, используя начальные условия:
при t = 0 (новое начало отсчета времени) x = 0 ,			y = 0 , x = vB cosα ,

y = vB sin α . Откуда

C3 = vB cosα ; C4 = vB sin α ;

C5 = C6 = 0 .

С учетом значений постоянных интегрирования уравнения (6) перепишем следующим образом:

x = vB cosα ;

y = g t + vB sin α ; x = vB t cosα ;

y =	g	t 2	+ vB t sin α .	(7)

2

Координаты точки C : x = d , y = h , при этом угол между векторами vGC и vCy равен углу наклона участка DE к горизонту, т. е. β (по условию задачи вектор vGC перпендикулярен наклонному участку DE ), поэтому

vCx	= tgβ ,	(8)
vCy

где vCx = xT , а vCy = yT – проекции скорости камня соответственно на координатные оси Bx и By в момент времени T , т. е. когда он достигает

точки C .
Уравнения (7) для момента времени t = T						перепишем с учетом (8)
следующим образом:
tgβ =				vB cosα
					;
			g T + vB sin α
d = vB T cosα ;
h =	g			T 2 + vB T sin α .			(9)

2
Подставим в (9) известные по условию задачи данные:
tg20 =				vB cos30		;
		9,8 T + vB sin 30

1 = vB T cos30 ;

			23
h =	9,8	T 2	+ vB T sin 30 .	(10)
h =	2	T 2	+ vB T sin 30 .	(10)
	2

Решая уравнения (10) совместно получим, что vB = 2,454 м/с;

T = 0,470 с; h = 1,659 м.

Подставим скорость vB в уравнения (4): 2,454 = 4,051 τ + vA ; 0,7 = 2,026 τ2 + vA τ ,

после решения которых, отбрасывая отрицательные корни, получим, что

τ= 0,459 с;

vA = 0,595 м/с.

Ответ: vA = 0,595 м/с, h = 1,659 м.

Пример выполнения задания Д2

	Дано: m1 – масса груза 1; m2 = 2 m1 – масса блока 2; m3 = 3 m1 –
масса барабана 3; m4						= 2 m1 – масса шатуна 4; R2 = 20 см – радиус блока
2; r	= R	2	и R =	3	R	2	– радиусы барабана 3; i	3	= 30 см – радиус инерции

3			3	2

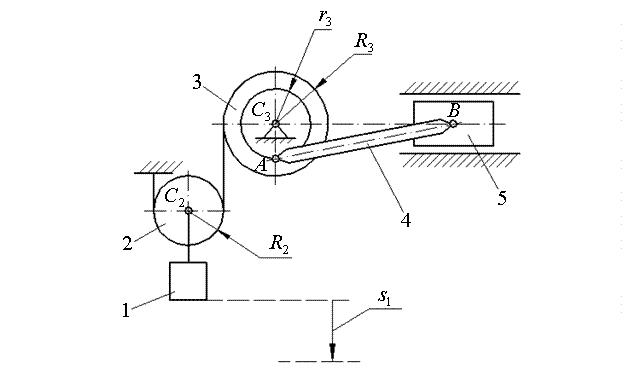
барабана 3; AB = l = 2 R2 – длина шатуна 4 (рисунок 5).

Массой ползуна 5 пренебречь. Шатун 4 считать однородным тонким стержнем, а блок 2 – однородным сплошным цилиндром.

Груз 1 из состояния покоя переместился вниз на расстояние s1 = 15 π см.

Найти: скорость v1 груза 1 в конечном положении.

Решение

Применим теорему об изменении кинетической энергии, считая, что система состоит из твердых тел и нерастяжимой нити:

T − T0 = ∑ AiE ,

(11)

где T – кинетическая энергия системы в конечном положении; T0 – кинетическая энергия системы в начальном положении;

∑ AiE – сумма работ внешних сил, действующих на систему во

время ее движения. Так как система начала движение из состояния покоя, то T0 = 0, и уравнение (11) принимает вид:

T = ∑ AiE .

Рисунок 5– Исходная схема

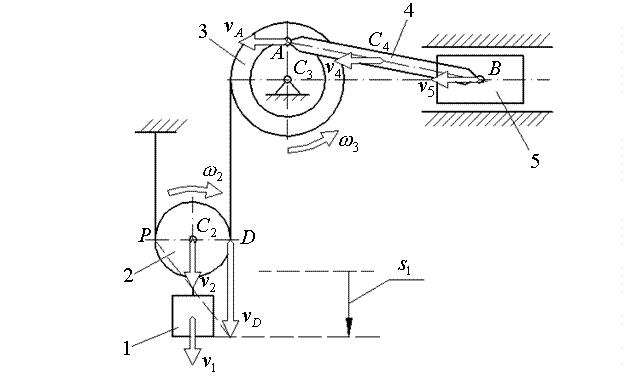
Определим сначала левую, а затем правую часть уравнения (11). Для этого изобразим систему в конечном положении (рисунок 6).

Кинетическая энергия системы в конечном положении

	T = T1 + T2 + T3 + T4 ,	(12)
где T1 – кинетическая энергия груза 1;
T2	– кинетическая энергия блока 2;
T3	– кинетическая энергия барабана 3;
T4	– кинетическая энергия шатуна 4.

Так как груз 1 движется поступательно, то его кинетическую энергию найдем по формуле

T =	m v2
	1 1	.	(13)

1	2

Кинетическая энергия блока 2, совершающего плоское движение,

		m	2	v2		JC	2	ω22
T	=		2	2	+		2		,	(14)
T	=				+				,	(14)
2				2				2
				2				2

где v2 – скорость центра масс (точки C2 ) блока 2;

JC2 – момент инерции блока 2 относительно оси, проходящей через точку C2 перпендикулярно плоскости схемы;

ω2 – угловая скорость плоского движения блока 2.

Рисунок 6 – Схема системы в конечном положении

Кинетическая энергия барабана 3, совершающего вращательное движение вокруг неподвижной оси,

(проходящей через точку C3 перпендикулярно плоскости схемы); ω3 – угловая скорость вращения барабана 3.

Шатун 4, как и блок 2, совершает плоское движение. Его кинетическая энергия

		m	4	v2		JC	4	ω42
	T =		4	4	+		4		,	(16)
	T =				+				,	(16)
	4			2				2
				2				2
где v4	– скорость центра масс (точки C4 ) шатуна 4;
JC4	– момент инерции шатуна 4 относительно оси, проходящей
через точку C4 перпендикулярно плоскости схемы;
ω4	– угловая скорость плоского движения шатуна 4.
Найдем кинематические соотношения между линейными и угловыми

скоростями и перемещениями точек системы и выразим их соответственно

через искомую скорость v1 и перемещение s1			груза 1.
Скорость центра масс блока 2 равна скорости груза 1, т. е.
v2 = v1 .			(17)
Угловая скорость блока 2
ω2 =	v2	,
	C2 P

где C2 P – расстояние от центра масс блока 2 до мгновенного центра скоростей (МЦС), т. е. точки P .

Так как C2 P = R2 , то ω2

. В итоге

ω2

(18)

Скорость

точки

раза больше

скорости v2 :

= ω

DP =

2 R

= 2 v . В итоге

vD = 2 v1 .

Угловая

скорость

барабана

(с

учетом того,

что по условию

R =

)

ω = vD =

2 v1

4 v1

3 R2

В итоге

4 v1

ω3

(19)

3 R2

Обозначив угол поворота барабана как ϕ3 , произведем следующие

замены в формуле (19):

dϕ3

ω3

;

ds1

после чего получим, что

dϕ3

ds1

;

3 R2

dϕ3

ds1 .

3 R2

После интегрирования при нулевых начальных условиях получаем,

что

ϕ3

s1 .

3 R2

Если груз 1 переместиться на расстояние s1 = 15 π , то барабан 3 по-

вернется на угол ϕ3 =

4 15 π

= π , что и отражено на рисунке 7.

3 20

Скорость точки

A (с учетом того,

что по условию задачи

r3 = R2 )

= ω

r =

4 v1

v . В итоге

3 R2

v .

Так как скорости точек A и B параллельны, то в этот момент МЦС шатуна 4 находится в бесконечности, а поэтому его угловая скорость

ω4			= 0 ,					(20)
и скорость центра масс шатуна 4 v		4	= v		A	=	4	v . В итоге

						3		1

v	4		=	4	v .			(21)

			3			1

Подставим (17) и (18) в формулу (14), принимая во внимание, что момент инерции блока 2, т. е.

								JC2	=		m2 R22
								JC2	=	2
										2
и m2 = 2 m1		(см. условие задачи):
															R22	v1	2
			v2	JC	ω22			m v2					2	m1
	m		v2	JC	ω22		2	m v2					2	m1	2	R			3
T =		2	2 +		2	=		1	1 +							2		=		m	v2 .
T =		2	2 +			=		1	1 +									=		m	v2 .
2			2		2			2							2				2	1	1
			2		2			2							2				2
В итоге										3
								T	=	3		m v2 .									(22)
								T	=			m v2 .									(22)
								2		2			1	1
										2
Подставляем (19) в формулу (15) и учитываем, что
								JC	= m3 i32
									3

и m3 = 3 m1 (см. условие задачи):

		JC ω33				2			4 v	2		8		i2
		JC ω33		3 m1 i3				3 R				8		i2
								1
T	=	3	=						2		=		m	3	v2 .
T	=	2	=				2				=	3	m	R2	v2 .
3		2					2					3	1	R2	1
														2
В итоге							i32
			T =		8		i32		m v2 .
			T =						m v2 .
			3		3		R22	1		1
					3		R22

Учитывая, что m4 = 2 m1 (по условию задачи):

								4 v	2
	m v2	JC	4	ω42		2 m1		1			JC	0		16
T =	4 4 +		4		=			3		+		2	=		m	v2 .
T =	4 4 +				=					+			=		m	v2 .
4	2			2			2				2			9	1	1
	2			2			2				2			9

В итоге

T4 = 169 m1 v12 .

Преобразуем формулу (12):

(23)

(24)

	1		v2		3		v2		8	i2		v2		16		v2		34	R2	+	24	i2		v2
T =		m		+		m		+		3	m		+		m		=		2			3	m		=
T =		m		+		m		+			m		+		m		=						m		=
	2	1	1		2	1	1		3	R22	1	1		9	1	1			R22			1		1
	2				2				3	R22				9					R22

=	34 20	2 + 24 25		2		m v2		=	143	m	v2 .
=						m v2		=		m	v2 .
		202			1		1		2	1	1
		202							2
В итоге			143
		T =	143			m v2 .					(25)
		T =				m v2 .					(25)
			2		1		1
			2

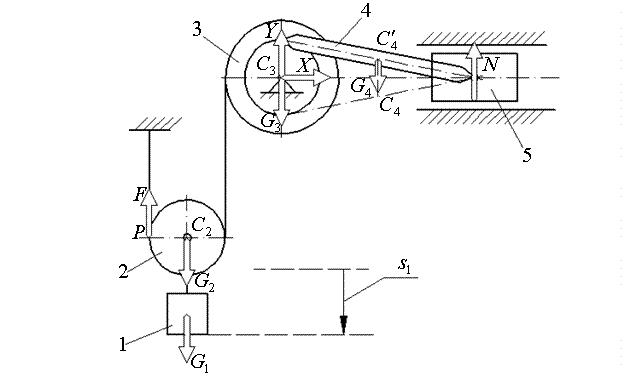
Найдем теперь сумму работ внешних сил. Покажем внешние силы на схеме (рисунок 7).

Рисунок 7 – Схема действия сил на систему

Работа силы TG натяжения троса равна 0, т. к. она приложена в неподвижной в данный момент точке P – МЦС. Работы силы тяжести G3 и реакций XG и YG, действующих на барабан 3, также равны 0, т. к. точка C3

их приложения неподвижна. Работа реакции N равна 0, т. к. данная сила составляет 900 с направлениемG смещения ее точки приложения.

Работа силы G1 , действующей на груз 1:

				AG			= m g s			.			(26)
Работа силы тяжести GG					G1		1	1
Работа силы тяжести GG				2 , действующей на блок 2:
			A G = m		2	g s = 2 m g s .
			G2		2		1			1			1
В итоге			A G		= 2 m g s					.			(27)
			A G		= 2 m g s					.			(27)
			G2				1	1
Работа силы тяжести G4 , действующей на шатун 4:
				G						′
			AG4		= −m4 g C4C4 ,
где							′	= r3 ,
							′
							C4C4
откуда A G	= −m	4	g r = −2 m g R						2	.
G4		4	3				1		2
В итоге				A G			= −2 m g R					.	(28)
				A G			= −2 m g R				2	.	(28)
						G4		1			2

Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (26)–(28):

∑ AE	= AG + AG + AG = m g s + 2 m g s − 2 m g R									2	=
i	G1		G2	G4	1	1	1	1	1	2
= (3 s − 2 R		2	) m g = (3 15 π − 2 20) 10−2					m g = 1,014 m g .
1		2	1					1		1
В итоге				∑ AiE = 1,014 m1 g .
				∑ AiE = 1,014 m1 g .							(29)

Приравняем значения T и ∑ AiE , определяемые по формулам (25) и (29) соответственно:

	143			m v2		= 1,014 m g ,

		2	1		1	1
откуда

v =				2 1,014 9,8 = 0,373 м/с.
1			143

Ответ: v1 = 0,373 м/с.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете Теоретическая механика

#
29.02.2016647.8 Кб66Теоретическая механика.pdf
#
29.02.2016724.38 Кб44Теоретическая механика2.pdf

	1		v2		3		v2		8	i2		v2		16		v2		34	R2	+	24	i2		v2
T =		m		+		m		+		3	m		+		m		=		2			3	m		=
T =		m		+		m		+			m		+		m		=						m		=
	2	1	1		2	1	1		3	R22	1	1		9	1	1			R22			1		1
	2				2				3	R22				9					R22

	1		v2		3		v2		8	i2		v2		16		v2		34	R2	+	24	i2		v2
T =		m		+		m		+		3	m		+		m		=		2			3	m		=
T =		m		+		m		+			m		+		m		=						m		=
	2	1	1		2	1	1		3	R22	1	1		9	1	1			R22			1		1
	2				2				3	R22				9					R22

	1		v2		3		v2		8	i2		v2		16		v2		34	R2	+	24	i2		v2
T =		m		+		m		+		3	m		+		m		=		2			3	m		=
T =		m		+		m		+			m		+		m		=						m		=
	2	1	1		2	1	1		3	R22	1	1		9	1	1			R22			1		1
	2				2				3	R22				9					R22