
08M028
.pdf
Первый частный случай (рис.7).
АВ = l r = 0
d1 = 32 l cos α
R1Ф = 21 mω2l sin α
Рис.7
Второй частный случай (рис.8).
АВ = l
α = 0 d 2 = 21 l
R 2Ф = m ω 2 r
Рис.8
2. Тяжелая окружность.
На рис.9 изображена тяжелая окружность массой m в вертикальной плоскости, которая вращается вокруг вертикальной оси с постоянной скоростью ω. Радиус R окружности известен;
ОС = 12 R .
11

Пусть масса окружности m = γ2πR , где γ = |
m |
- погонная |
|
2πR |
|||
|
|
масса дуги окружности в кг/м.
Данную окружность разбиваем на две части: 1 и 2. Дуга 1 окружности будет располагаться слева от оси Oz , дуга 2 - справа от той же оси.
|
|
|
|
|
|
Рис.9 |
|
|
|
|
|
|
|
Масса дуги любой длины определится формулой |
|
|
|||||||||||
|
|
m = |
mSi |
. |
|
|
|
|
|
|
(16) |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
i |
|
2πR |
|
|
|
|
|
|
|
||
При длине дуг |
S = 2α R |
, S |
= 2α |
R , α = π |
3 |
, α |
2 |
= 2π |
3 |
определим |
|||
|
1 |
1 |
2 |
2 |
1 |
|
|
|
|||||
их массу по формуле (16).
Тогда m1 = 13 m , m2 = 2 3 m .
Далее определяем координаты центров тяжестей этих дуг по следующим формулам
x1 = R sinα1 , x2 = R sinα2 .
α1 α2
Окончательно запишем: x1 = 0,827R; x2 = 0,414R. Теперь определяем расстояние от центров тяжести дуг S1 и S2 до оси Оz.
r1 = x1 - 0,5R = 0,327R , r2 = x2 + 0,5R = 0,914R .
12

Вычисляем нормальные ускорения для точек С1 и С2
an |
= ω2r = 0,327ω2R , |
c |
1 |
1 |
|
an |
= ω2r = 0,914ω2R . |
c2 |
2 |
Определяем |
Rф |
и |
|
Rф |
|
||||
1 |
|
|
|
|
2 |
|
|||
Rф = m an |
= 1 |
3 |
m 0,327ω2R ≈ 0,11mω2R , |
||||||
1 |
1 |
c1 |
|
|
|
|
|
||
Rф = m an |
|
= 2 |
3 |
m 0,914ω2R ≈ 0,61mω2R . |
|||||
2 |
2 |
c2 |
|
|
|
|
|
||
Результирующий вектор Rф = Rф - Rф ; |
|||||||||
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
Rф = 0,5mω2R . |
(17) |
|||||
Вывод: при вращении тяжелой окружности со смещением ее центра относительно неподвижной оси главный вектор сил инерций будет определяться через ускорение центра этой окружности и ее массу.
Если центр тяжелой окружности будет лежать на неподвижной оси, то Rф = 0 .
3. Часть дуги тяжелой окружности.
Рассмотрим случай, когда часть дуги тяжелой окружности вращается вокруг вертикальной неподвижной оси с постоянной угловой скоростью ω (рис.10).
Дуга OA = S стягивается известным углом α, а радиус окружности равен R и масса m этой дуги задана.
На дуге 1 выделяем элементарную массу:
dm = ρds = ρRdj , где ρ= αmR - погонная масса дуги окружности
в кг/м.
Силы инерции дуги тяжелой окружности будем приводить к
точке А. Элементарная сила инерции |
d |
|
= dman . |
φ |
|||
|
|
|
k |
. |
|
|
|
13
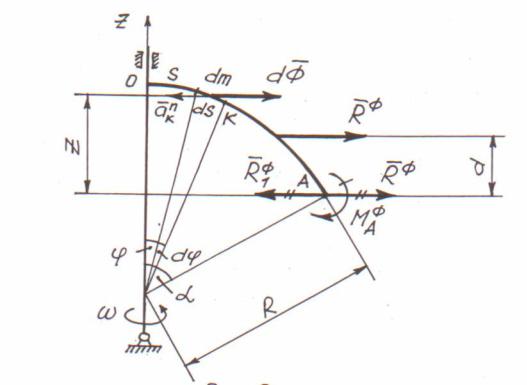
Рис.10
При an = ω2Rsinj и dm = ρRdj будем иметь |
|
||||||
k |
|
|
dφ= ρR2ω2sinj dj . |
|
|||
|
|
|
|
(18) |
|||
Главный вектор сил инерций |
|
||||||
|
|
α |
|
|
|
|
|
RФ = ∫dφ= ρR2ω2 ∫sinj dj . |
|
|
|||||
|
m |
0 |
|
|
|
|
|
С учетом ρ= |
окончательно запишем |
|
|||||
αR |
|
||||||
|
|
|
|
|
(1 - cosα) |
|
|
|
|
R |
Ф |
2 |
R |
(19) |
|
|
|
|
= mω |
α |
|||
|
|
|
|
|
|
|
|
Теперь запишем равенство для определения элементарного главного момента.
dMФA = dφ z .
При z = Rcosj - Rcosα
|
α |
|
dMAФ = ρR3ω2sinj (cosj - cosα)dj , MAФ = ∫dMФA . |
|
|
|
0 |
|
Окончательно получим формулу для вычисления |
|
|
MAФ = mω2R2 |
(1 - cosα)2 |
(20) |
2α |
|
|
14 |
|
|

Перпендикулярные между собой главный вектор RФ и главный момент MФA приведем к простейшему виду.
Главный момент представим парой сил так, чтобы сила пары была равна главному вектору RФ .
MФA = MA (RФ; R1Ф ); MФA = RФd ,
где d - плечо пары сил RФ и R1Ф.
Тогда в точке А MФA не будет, а RФ + R1Ф = 0 .
Систему сил инерций приведем к одной силе RФ , которая будет приложена в точке В, где расстояние по вертикали от точки А до точки В определится формулой
d = |
MФ |
|
|
|
|
A . |
|
|
|
|
|
|
RФ |
|
|
|
|
Окончательно запишем |
|
|
|
|
|
d = |
R (1+ cos2α - 2cosα) |
= 1 |
2 |
R (1 - cosα). |
(21) |
|
2 (1 - cosα) |
|
|
|
|
Формулы (21) и (19) - общие формулы для определения главного вектора RФ и точки его приложения.
Рассмотрим частные случаи.
• Первый частный случай.
Возьмем одну четвёртую часть тяжелой окружности (рис.9), для которой α = π 2 . Тогда
R1Ф = 2mπω2R и d1 = 12 R .
15

• Второй частный случай.
Для половины дуги тяжелой окружности α = π . Главный вектор
|
|
RФ = 2mω2R |
и d |
2 |
= R . |
|
|
||||
|
|
2 |
π |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Если рассматривать часть площади круга радиусом r, то для |
|||||||||||
|
|
|
Ф и точки его приложения будут |
||||||||
определения главного вектора |
R |
||||||||||
справедливы те же формулы (19) и (21), но при R = 2 |
3 |
r . |
|||||||||
|
|
|
(1 - cosα) |
|
|
|
|
|
|
|
|
RФ = 2 |
3 |
mω2r |
; |
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
d = r (1+ cos2α - 2cosα) |
= 1 |
3 |
r (1 - cosα) |
|
(22) |
||||||
|
|
3 (1 - cosα) |
|
|
|
|
|
|
|||
Литература
1.Бутенин Н.В., Лунц ЯЛ., Меркин Д.Р. Курс теоретической механики,
ч.2 – М.,1985г.
2. Ермаков Б.Е., Асриянц А.А. Теоретическая механика: теория, контрольные задания и примеры решения задач. Учебное пособие. Издание второе, исправленное и дополненное. МАДИ
(ГТУ) – М.,2003г.
16

Пример решения задачи
Четырехколесное самоходное транспортное средство 2 тянет груз 1 по прямолинейной траектории с ускорением a = 0,3 м/с2 при помощи каната СD, который наклонен к горизонту под углом α = 60°.
Заданы следующие величины: m1 = 1000 кг - масса груза 1; m2 = 4000 кг - масса корпуса машины; m3 = 100 кг - масса колеса; f1 = 0,2 - коэффициент трения скольжения между грузом и полотном дороги; r3 = r = 0,5 м - динамический радиус колеса.
Определить необходимый коэффициент трения сцепления колес с дорогой для режима чистого качения колес машины без скольжения, а также величину момента М пары сил, приложенной к заднему мосту транспортного средства.
Рис.11
Решение.
Для решения задачи используем принцип Даламбера и, в первую, очередь рассмотрим отдельно тело 1 (рис.12).
|
|
|
|
|
|
Y |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
N1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Ф |
|
|
|
|
|
|
|
|
|
S |
a |
||
|
R |
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
X |
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
F |
|
|
|
|
|
P |
|
|
|
||||
|
|
|
тр |
1 |
|
|
|
||||||||
Рис.12
На тело 1 действуют следующие силы: Р1 = m1g = 1000·9,8 = = 9800 Н = 9,8 кН - сила тяжести груза; N1 - реакция нормального
17

давления; S - усилие в канате; Fтр = N1f1 - сила трения скольжения
груза 1 относительно полотна дороги; R1Ф = m1a = 1000·0,3 = 300;
Н= 0,3 кН - главный вектор сил инерций.
Запишем два уравнения кинетостатики для тела 1.
|
n |
|
|
|
∑Fkx = 0 , Scosα - Fтр - R1Ф = 0 ; |
|
|
|
k=1 |
|
|
|
n |
|
|
|
∑Fky = 0 , Ssinα+ N1 - P1 = 0 . |
|
|
|
k=1 |
|
|
Или |
Scosα - N f - RФ = 0 |
|
|
|
1 1 |
1 |
|
|
Ssinα+ N1 - P1 = 0 . |
(23) |
|
Если второе уравнение умножим на f1 и сложим с первым уравнением системы (23), получим
S (cosα+ f1sinα)- R1Ф - P1f1 = 0 ,
|
|
P f + RФ |
|
|||
|
1 1 |
1 |
|
|
||
откуда S = |
|
|
(24) |
|||
cosα+ f sinα |
||||||
|
|
|
1 |
|
|
|
Подставим численные значения в формулу (24) |
||||||
S = |
|
9,8 0,2 + 0,3 |
3,36 кН. |
|||
cos60o + 0,2sin60o |
||||||
|
|
|||||
S = 3,36 кН.
Теперь рассмотрим движение самоходного транспортного средства без груза (рис. 13)
Y |
2 |
|
|
RФ |
1,2r |
|
3 |
α |
|
|
|
S′ |
М |
|
|
1,2r |
|
|
|
|
|
Ф |
|
C |
a |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
R |
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P3 |
3 |
||||
|
|
|
|
|
|
|
3 |
|
P2 |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
P3 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,4r |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
Ф |
|
|
|
|
|
Ф |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
Ф |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
NB |
|
|
Fд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
FAсц |
|
|
X |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2r |
Bсц |
|
|
|
4r |
|
|
N A |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
Рис.13
18

На конструкцию машины действуют следующие силы: P2 = m2 g = 39200 Н = 39,2 кН - сила тяжести корпуса машины;
P3 = m3 g = 980 Н = 0,98 кН - сила тяжести колеса; S′ = S = 3,36 кН - сила натяжения каната;
R2Ф = m2a =1200 Н = 1,2 кН - главный вектор сил инерций корпуса 2;
R3Ф = m3a = 30 Н = 0,03 кН - главный вектор сил инерций колес при его поступательном движении;
M Ф = J ε |
=1/ 2m r2 |
a |
= 0,5·100·0,5·0,3 = 7,5 Н·м = 0,0075 кН·м - |
|
|
||||
3 |
3 3 |
3 3 r |
||
|
|
3 |
||
момент от сил инерций колеса при вращательном его движении; FAдсц , FBдсц - силы трения сцепления колес с дорожным полотном;
NA , NB - реакция нормальных давлений, действующих со стороны опорной поверхности на все колеса машины.
Используя принципы Даламбера для плоской произвольной системы сил (рис.13), составим три уравнения кинетостатики:
∑MB (Fk )= 0 ;
S′ 1,2rcosα+ S′ 1,2rsinα+ 4R3Фr + 4M3Ф + +R2Ф 1,4r + 2NA 6r - P2 2r - 2P3 6r - M = 0 ;
∑Fkx = 0 ;
д |
д |
Ф |
Ф |
′ |
(25) |
2FВсц - 2FАсц - R2 |
- 4R3 |
- S cosα = 0 |
|||
∑Fky = 0 ;
2NA + 2NB - P2 - 4P3 - S′sinα = 0 .
В систему (25) подставим известные численные значения:
6NA - M = 41,4 ,
NA + NB = 23 , (26) FBдсц - FAдсц = 1,5 .
Трех уравнений системы (26) недостаточно для определения пяти неизвестных величин - M , N A , NB , FAдсц, FBдсц.
19
Поэтому рассмотрим отдельно движение заднего моста вместе с колесами машины (рис.14) и одного из колес переднего моста (рис.15).
r
2YO2
2R3Ф
O1 2XO2 2М3Ф
М
2NB 2FBдсц
Рис.14
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
Y2 |
|
|
||||
|
|
|
|
|
|
М3 |
||||
|
|
|
|
|
||||||
|
|
Ф |
|
O2 |
XO2 |
|||||
R |
||||||||||
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
P3 |
|
|
r |
|||
FAдсц A  N A
N A
Рис.15
На основе расчетных схем (рис.14 и рис.15) составим два уравнения кинетостатики
∑MO1 (Fk )= 0 , M - 2M3Ф - 2FBдсц r = 0 ;
∑MO2 (Fk )= 0 , -M + FAдсц r = 0 .
Если второе уравнение умножим на два и сложим с первым уравнением, то получим
20
