
Математика. Лаб. практикум. Ч
.1.pdf11
|
(n+1) |
|
(n) |
|
(n) |
|
|
x1 |
= |
−0,165x2 |
+ |
0,315x3 |
+0,669; |
||
x2(n+1) |
= 0,307x1(n) |
|
−0,443x3(n) |
+0,75; |
n = 0,1,2,... (8) |
||
x |
(n+1) |
= −0,481x(n) −0,013x(n) |
|
|
+ 2,058, |
||
|
3 |
1 |
2 |
|
|
|
|
Выбираем нулевое приближение ( x(0) |
, x(0) , |
x(0) ), равное свободным |
|||||
|
|
|
|
|
1 |
2 |
3 |
членам СЛАУ (8), к искомому решению (x1, x2 , x3 ) СЛАУ (1): |
|||||||
|
|
x(0) |
= 0,669 , x(0) |
= 0,75 , x(0) = 2,058 . |
|||
|
|
1 |
|
2 |
|
3 |
|
2.3 Нахождение решения (x1; x2 ; x3 ) с заданной точностью. Вычис-
ляя по формулам (8), находим решение (x1; x2 ; x3 ) с заданной точностью ε. Оканчиваем расчет, если выполняются неравенства:
|
|
|
|
x(n+1) |
− x(n) |
≤ε, i = |
|
. |
(9) |
|
|
|
|
1,3 |
|||||
|
|
|
|
i |
i |
|
|
|
|
Шаг1. При n = 0 из(8) находимпервоеприближениекрешениюСЛАУ(1) |
|
||||||||
x(1) |
= −0,165x(0) |
+0,315x(0) |
+0,669 = −0,165 0,75 +0,315 2,058 +0,669 ≈1,194; |
||||||
1 |
2 |
3 |
|
|
|
|
|
|
|
x(1) |
= 0,307x(0) −0,443x(0) +0,75 = 0,307 0,669 −0,443 2,058 +0,75 ≈ 0,044; |
|
|||||||
2 |
1 |
3 |
|
|
|
|
|
|
|
x(1) |
= −0,481x(0) |
−0,013x(0) |
+2,058 = −0,481 0,669 −0,013 0,75 +2,058 ≈1,746. |
||||||
3 |
1 |
2 |
|
|
|
|
|
|
|
Шаг2. При n =1 из(8) находимвтороеприближениекрешениюСЛАУ(1): x1(2) = −0,165x2(1) +0,315x3(1) +0,669 = −0,165 0,044 +0,315 1,746 +0,669 ≈1,212;
x2(2) = 0,307x1(1) −0,443x3(1) +0,75 = 0,307 1,194 −0,443 1,746 +0,75 ≈ 0,343;
x3(2) = −0,481x1(1) −0,013x2(1) +2,058 = −0,481 1,194 −0,013 0,044 +2,058 ≈1,484.
Шаг3. При n = 2 из(8) находимтретьеприближениекрешениюСЛАУ(1): x1(3) = −0,165x2(2) +0,315x3(2) +0,669 = −0,165 0,343 +0,315 1,484 +0,669 ≈1,08;
x2(3) = 0,307x1(2) −0,443x3(2) +0,75 = 0,307 1,212 −0,443 1,484 +0,75 ≈ 0,465;
x3(3) = −0,481x1(2) −0,013x2(2) + 2,058 = −0,481 1,212 −0,013 0,343 + 2,058 ≈1,479.
Шаг 4. При n = 3 из (8) находим четвертое приближение к решению СЛАУ (1):
x1(4) = −0,165x2(3) +0,315x3(3) +0,669 = −0,165 0,465 +0,315 1,479 +0,669 ≈1,058; x2(4) = 0,307x1(3) −0,443x3(3) +0,75 = 0,307 1,08 −0,443 1,479 +0,75 ≈ 0,426;
x3(4) = −0,481x1(3) −0,013x2(3) +2,058 = −0,481 1,08 −0,013 0,465 +2,058 ≈1,544.
Шаг 5. При n = 4 из (8) находим пятое приближение к решению СЛАУ (1): x1(5) = −0,165x2(4) +0,315x3(4) +0,669 = −0,165 0,426 +0,315 1,544 +0,669 ≈1,085;
x2(5) = 0,307x1(4) −0,443x3(4) +0,75 = 0,307 1,058 −0,443 1,544 +0,75 ≈ 0,391;
x3(5) = −0,481x1(4) −0,013x2(4) +2,058 = −0,481 1,058 −0,013 0,426 +2,058 ≈1,554.

12
Шаг6. При n = 5 из(8) находимшестоеприближениекрешениюСЛАУ(1): x1(6) = −0,165x2(5) +0,315x3(5) +0,669 = −0,165 0,391+0,315 1,554 +0,669 ≈1,094;
x2(6) = 0,307x1(5) −0,443x3(5) +0,75 = 0,307 1,085 −0,443 1,554 +0,75 ≈ 0,395;
x3(6) = −0,481x1(5) −0,013x2(5) +2,058 = −0,481 1,085 −0,013 0,391 +2,058 ≈1,541.
Шаг7. При n = 6 из(8) находимседьмоеприближениекрешениюСЛАУ(1):
x(7) |
= −0,165x(6) |
+0,315x(6) +0,669 = −0,165 0,395 +0,315 1,541 +0,669 ≈1,089; |
|||||
1 |
2 |
3 |
|
|
|
|
|
x(7) |
= 0,307x(6) −0,443x(6) +0,75 = |
0,307 1,094 −0,443 1,541 +0,75 ≈ 0,403; |
|||||
2 |
1 |
3 |
|
|
|
|
|
x(7) |
= −0,481x(6) |
−0,013x(6) +2,058 = −0,481 1,094 −0,013 |
0,395 +2,058 ≈1,537. |
||||
3 |
1 |
2 |
|
|
|
|
|
|
Полученные результаты представлены в таблице 1. |
|
|
||||
|
Таблица 1 – Результаты вычислений |
|
|
||||
|
|
|
|
|
|
|
|
|
n |
|
x1(n+1) |
|
x2(n+1) |
x3(n+1) |
|
|
0 |
|
0,669 |
|
0,75 |
2,058 |
|
|
1 |
|
1,194 |
|
0,044 |
1,746 |
|
|
2 |
|
1,212 |
|
0,343 |
1,484 |
|
|
3 |
|
1,08 |
|
0,465 |
1,479 |
|
|
4 |
|
1,058 |
|
0,426 |
1,544 |
|
|
5 |
|
1,085 |
|
0,391 |
1,554 |
|
|
6 |
|
1,094 |
|
0,395 |
1,541 |
|
|
7 |
|
1,089 |
|
0,403 |
1,537 |
|
Заканчиваем вычисления, т. к. выполнены условия (9):
x(7) |
− x(6) |
|
= |
|
1,089 |
−1,094 |
|
|
= 0,005 <ε =10−2 , |
|||
|
|
|
||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
x(7) |
− x(6) |
|
= |
|
0,403 −0,395 |
|
= 0,005 <ε =10−2 , |
|||||
|
|
|
||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
x(7) |
− x(6) |
|
= |
|
1,537 |
−1,541 |
|
= 0,004 <ε =10−2. |
||||
|
|
|
||||||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверку на компьютере можно выполнить двумя способами:
– решаем СЛАУ (1) методом Гаусса и получаем результат:
x1 |
≈1,085; |
x2 |
≈ 0,4052; |
x3 ≈1,531 ; |
|
– решаем |
СЛАУ |
(6) методом итераций и получаем результат: |
|
x1 |
≈1,089; |
x2 |
≈ 0,403; |
x3 ≈1,536. |
3Ответ: x1 = x1(8) ≈1,08; x2 = x2(8) ≈ 0,40; x3 = x3(8) ≈1,53 – решение
СЛАУ (1).
4Варианты заданий даны в лабораторной работе № 1 «Решение системы линейных алгебраических уравнений методом Гаусса».
13
Лабораторная работа № 3. Приближенное решение уравнения вида f (x)= 0 методом половинного деления
Пусть задана непрерывная функция f (x) и требуется найти корень уравнения f (x)= 0 . Предположим, что найден отрезок [a;b] такой, что f (a) f (b)< 0 . Тогда согласно теореме Больцано-Коши внутри отрезка [a;b] существует точка k , в которой значение функции равно нулю, т. е. f (k )= 0, k (a;b) . Итерационный метод бисекций (половинного деле-
ния) |
состоит |
в построении последовательности вложенных отрезков |
||||||||||||
[a |
n |
;b |
] |
|
[a |
n |
;b |
] [a |
n−1 |
;b |
] [a;b] |
} |
, на концах которых функция прини- |
|
|
||||||||||||||
{ |
|
n |
|
|
|
n |
|
n−1 |
|
|
||||
мает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти нуль функции f (x) (корень x уравнения
f(x)= 0 ) с любой заданной точностью.
1Постановка задачи. Определить количество действительных корней уравнения
x3 + x2 −3 = 0 , |
(1) |
отделить эти корни и, применив метод половинного деления, вычислить их с точностью 0,01.
2 Графический метод. Можно построить график функции |
|
y = x3 + x2 −3 , |
(2) |
и корнями уравнения (1) будут абсциссы точек пересечения графика функ-
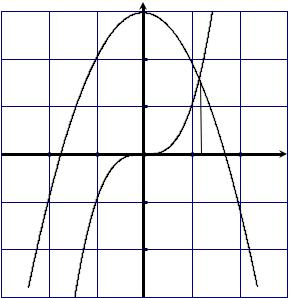
ции (2) с осью Ox . Но проще записать уравнение (1) в виде x3 = 3 − x2 , корнями уравнения (1) будут абсциссы точек пересечения двух кривых y = x3 и y = 3 − x2 (рисунок 1).
3 Метод половинного деления.
Для того чтобы применить метод половинного деления, необходимо выполнение следующих условий:
1)f (x) непрерывна на [a;b];
2)f (a) f (b)< 0;
3)f ′(x)сохраняет знак на [а;b]
4)f ′′(x) сохраняет знак на [a;b]
на [a;b] выпукл или вогнут).
(f (x)монотонна на [a;b]); (3)
(график функции y = f (x)
14
y
|
|
|
|
y = x3 |
y = 3 − x2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x |
-2 |
-1 |
0 |
1 |
2 x |
-1
Рисунок 1
Проверим, можно ли применить метод половинного деления для вычисления корня x [1; 1,5] уравнения (1).
1)f (x)= x3 + x2 −3 непрерывна на [1; 1,5];
2)f (1)= −1 < 0; f (1,5)=1,53 +1,52 −3 = 2,625
3)f ′(x)=3x2 + 2x > 0 для x [1; 1,5], значит,
функция f (x)возрастает на [1; 1,5];
4) f ′′(x)= 6x + 2 > 0 для x [1; 1,5], значит,
график функции f (x)вогнут на [1; 1,5].
> 0;
(4)
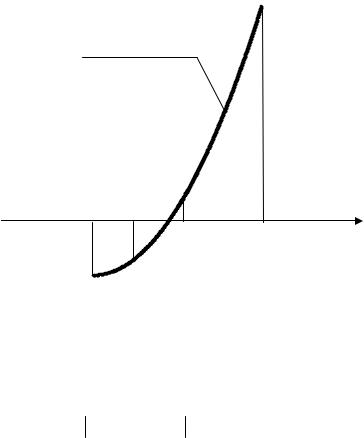
Учитывая условия (4), строим рисунок 2.
Из условия (4) заключаем, что на отрезке [1; 1,5] находится только
один корень уравнения (1).
Уточним значение корня x [1; 1,5] методом половинного деления
(вычислим его с заданной точностью ε =10−2 ).
x [1; 1,5], c1 = 1+21,5 =1,25, f (1,25)=1,253 +1,252 −3 ≈ 0,516 > 0 ;
x [1; 1,25], c2 = |
1 +1,25 |
=1,125 , |
f (1,125) =1,1253 +1,1252 −3 ≈ −0,31 < 0 ; |
|
|
|
2 |
|
|
x [1,125; 1,25], |
c3 |
= 1,125 +1,25 |
≈1,187, f (1,187)≈ 0,081 > 0 ; |
|
|
|
|
2 |
|
|
|
|
|
15 |
|
|
x [1,125; 1,187], |
c4 |
= |
1,125 +1,187 |
≈1,156 , |
f (1,156) ≈ −0,089 < 0 |
; |
|
|
|
2 |
|
|
|
x [1,156; 1,187], |
c5 |
= |
1,156 +1,187 |
≈1,172 , |
f (1,172) ≈ −0,013 < 0 |
; |
|
|
|
2 |
|
|
|
x [1,172; 1,187], |
c6 |
= |
1,172 +1,187 |
≈1,179 , |
f (1,179)≈ 0,029 > 0 ; |
|
x [1,172; 1,179]. |
|
|
2 |
|
|
|
|
|
|
|
|
|
B (1,5; 2,625)
y = x3 + x2 −3
a =1 c2 x |
|
x |
|
c1 |
b =1,5 |
||
|
A(1; −1)
Рисунок 2
Вычисляя корень x с заданной точностью, сохраняли в промежуточных вычислениях один запасной десятичный знак. Окончили вычисления, т. к.
1,179 −1,172 = 0,007 < 0,01.
Получили |
x = 1,172 +1,179 ≈1,175 . |
|
2 |
Результат, полученный на компьютере: x ≈1,1748. |
|
4 Ответ: |
x ≈1,17 – корень уравнения (1), вычисленный с точно- |
стью 0,01.
16
5 Варианты заданий к лабораторной работе № 3:
1) |
x −sin x = 0,75; |
11) |
3x −cos x −1 = 0 ; |
21) |
2x −lg x = 7 ; |
||||||||||||||||||||||
2) |
x2 +4sin x =1; |
12) |
x lg x −1,2 = 0 ; |
|
22) |
x3 + 2x + 4 = 0 ; |
|||||||||||||||||||||
3) |
2lg x − |
x |
+1 = 0; |
13) |
x3 − x −5 = 0 ; |
|
|
23) |
sin (x +1)= 0,5x ; |
||||||||||||||||||
3 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4) |
(x +1)2 |
|
= 0,5ex ; |
14) |
2ex −2x −3 = 0 ; |
24) |
e−2 x −2x +1 = 0; |
||||||||||||||||||||
5) |
x lg |
( |
x +1 =1; |
|
cos(x |
+ |
0,5) |
= |
|
3 |
|
x |
|
|
|
|
|
|
|||||||||
15) |
x ; |
25) |
2e +3x +1 = 0 ; |
||||||||||||||||||||||||
|
|
|
|
|
) |
|
|
|
|
||||||||||||||||||
6) |
x4 − x −1 = 0 ; |
16) |
sin (x +0,5)= 2x −0,5 ; |
26) |
(2 − x)ex |
= 0,5 ; |
|||||||||||||||||||||
7) |
ln x +(x +1)3 = 0 ; |
17) |
0,5x −lg (x +1)= 0,5; |
27) |
lg (2 + x)+2x = 3 ; |
||||||||||||||||||||||
8) |
2x +lg x = −0,5; |
18) |
2x +cos x = 0,5 ; |
28) |
ln x + x2 |
= 0 ; |
|||||||||||||||||||||
9) |
x2 +ln x −4 = 0 ; |
19) |
2sin (x +0,5)=1,5 − x ; |
29) |
sin |
x |
+1 = x2 ; |
||||||||||||||||||||
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
|
|
2 |
|
|
20) x |
2 |
= ln |
( |
x +1 |
|
; |
|
|
30) |
5sin x |
= |
x |
− |
1. |
||||||
10) e |
+ x |
|
|
−2 = 0 ; |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
) |
|
|
|
|
|
|||||||||||||||

17
Лабораторная работа № 4. Приближенное решение уравнения вида f (x)= 0 методом хорд и касательных (комбинированный метод)
1 Постановка задачи. Определить количество действительных кор-
ней уравнения |
|
x3 + x2 −3 = 0 , |
(1) |
отделить эти корни и, применив метод хорд и касательных, вычислить их с точностью ε =10−5 .
2 Отделение действительных корней уравнения (1) графическим методом (лабораторная работа № 3, п. 2).
3 Вычисление действительного корня x [1; 1,5] методом хорд и
касательных с заданной точностью ε =10−5 .
Для того чтобы применить комбинированный метод, необходимо выполнение следующих условий:
1)f (x) непрерывна на [a;b];
2)f (a) f (b)< 0;
3)f ′(x)сохраняет знак на [а;b]
4)f ′′(x) сохраняет знак на [a;b]
на [a;b] выпукл или вогнут).
(f (x)монотонна на [a;b]); (2)
(график функции y = f (x)
Проверим, можно ли применить метод хорд и касательных для вычисления корня x [1; 1,5] уравнения (1).
1) f (x)= x |
3 |
+ x |
2 |
−3 |
|
|
|
|
|
|
|
|
|
||
|
|
непрерывна на 1; 1,5 |
; |
|
|
||||||||||
( ) |
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) f 1 =−1<0; |
f |
1,5 =2,625 >0; |
|
|
|
(3) |
|||||||||
|
|
|
|||||||||||||
3) f ′(x)=3x |
2 |
+2x > |
0 |
|
|
|
|
; |
|
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||
|
для x 1; 1,5 |
|
|
||||||||||||
4) f ′′(x)=6x +2 >0 |
|
|
|
|
. |
|
|
|
|
||||||
для x 1; 1,5 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
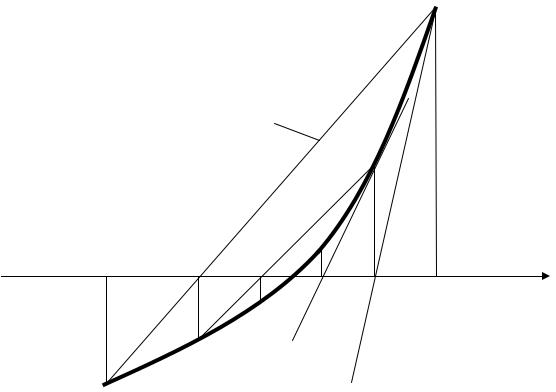
Учитывая условия (3), строим рисунок 1.
Расчетные формулы метода хорд и касательных имеют вид: a1 = a0 − ff ′((aa00));
b =b − |
f (b0 )(a0 −b0 ) |
и т. д. |
|||
f (a |
)− f (b |
) |
|||
1 0 |
|
||||
|
0 |
0 |
|
|
|
|
y − f (b0 ) |
|
|
x −b |
|
|
|
|
f (a )− f (b ) |
= a −b |
|
||||
|
|
|
|
|
0 |
|
|
|
0 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
b1 b2
b0 =1
B2
B1
B (b0 ; f (b0 ))
18
A(a0 ; f (a0 ))
A1
A2 |
|
|
x a2 |
a1 1,5 = a0 |
х |
y − f (a0 ) = f ′(a0 )(x −a0 )
Рисунок 1
За приближенное значение корня |
~ |
принимаем |
|
|
|
||||||||||
x |
|
|
|
||||||||||||
|
an+1 +bn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ≈ |
, |
|
если |
|
an+1 −bn+1 |
|
≤ ε, |
|
|
|
|||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (a |
|
) |
|
|
|
|
|
|
|
|
|
где an+1 = an − |
|
n |
= an + |
an , |
|
|
(4) |
||||||||
|
|
|
|
|
|
||||||||||
|
f ′(an ) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
f (bn )(an −bn ) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bn+1 = bn − f (a |
|
|
)− f (b ) = bn + |
bn . |
|
|||||||||
|
n |
|
|
||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||
Заметим, что на рисунке 1 |
обозначили a0 |
=1,5 |
и b0 =1 , т. к. хорды |
||||||||||||
проводят со стороны вогнутости графика функции, а касательные – с противоположной стороны.
Уточним корень x комбинированным методом (т. е. вычислим его с заданной точностью ε =10−5 ) по формулам (4). Вычисляя, будем сохра-
нять один запасной десятичный знак. Результаты вычислений представлены в таблице 1.

19
|
Таблица 1 – Вычисление корня уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = − |
f (an ) |
; |
|
||
|
|
|
|
3 |
2 |
|
|
|
|
|
′(an ) |
|
2 |
|
|
|
– |
|
|
|
|
|
f ′(an ) |
|||||||
|
|
|
|
|
−3 |
f |
|
+ |
2an |
|
|
|
|
|
|
n |
|
|
|
|||||||||||
n |
|
|
f (an )= an |
+ an |
|
= 3an |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
bn |
f (b |
)= b3 |
+b2 |
|
−3 |
|
f (a |
|
)− f |
(b |
) |
f (b |
)(a |
|
−b |
) |
|
b |
= − |
f (bn )(an −bn ) |
||||||||||
|
|
|
n |
n |
n |
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
n |
|
f (an )− f |
(bn ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
a0 |
=1,5 |
|
|
|
2,625 |
|
|
|
|
|
|
9,75 |
|
|
|
– |
|
|
|
|
–0,269230 |
|
|
||||||
b0 |
=1 |
|
|
|
–1 |
|
|
|
|
|
|
|
3,625 |
|
|
|
–0,5 |
|
|
|
0,137930 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
1,230770 |
|
|
|
0,379152 |
|
|
|
|
|
7,005910 |
|
|
– |
|
|
|
|
–0,054119 |
|
|
|||||||||
1,137930 |
|
|
–0,231623 |
|
|
|
|
|
0,610775 |
|
–0,021503 |
|
|
|
0,035307 |
|
|
|||||||||||||
2 |
1,176651 |
|
|
|
0,013583 |
|
|
|
|
|
6,506810 |
|
|
– |
|
|
|
|
–0,002087 |
|
|
|||||||||
1,173137 |
|
|
–0,009215 |
|
|
|
|
|
0,022798 |
|
–0,000032 |
|
|
|
0,001430 |
|
|
|||||||||||||
3 |
1,174564 |
|
|
|
0,000029 |
|
|
|
|
|
6,487929 |
|
|
– |
|
|
|
|
–0,000005 |
|
|
|||||||||
1,174557 |
|
|
–0,000016 |
|
|
|
|
|
0,000045 |
|
|
0 |
|
|
|
|
|
0 |
|
|
||||||||||
4 |
1,174559 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,174557 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Условие |
|
an+1 − bn+1 |
|
= |
|
a4 |
− b4 |
|
= 0, 000002 < 0, 00001 |
выполнено, |
на- |
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
ходим
x = a4 2+b4
Результат, полученный на компьютере: x ≈1,174553 .
4 Ответ: x ≈ 1,17455 –корень уравнения (1), получен с точностью 10−5 .
5 Варианты заданий даны в лабораторной работе № 3 «Приближенное решение уравнения вида f (x)=0 методом половинного деления».
20
Лабораторная работа № 5. Приближенное решение уравнения вида f (x) = 0 методом итераций
Метод простых итераций (метод последовательных приближений) решения уравнения f (x ) = 0 состоит в замене исходного уравнения экви-
валентным ему уравнением x =ϕ(x) и построении последовательности
xn+1 =ϕ(xn ) , сходящейся при n → ∞ к точному решению. Сформулируем |
||||||||
достаточные условия сходимости метода простых итераций. |
||||||||
Теорема. Пусть функция ϕ (x) |
определена и дифференцируема на |
|||||||
[a;b] , причем все ее значения ϕ (x) [a;b] |
. Тогда, если существует число |
|||||||
q , такое, что |
|
ϕ′(x) |
|
|
≤ q <1 на отрезке |
[a;b] , |
то последовательность |
|
|
|
|||||||
xn+1 =ϕ(xn ) (n = 0, 1, 2, ...) сходится к |
единственному на [a;b] решению |
|||||||
уравнения x =ϕ(x) при любом начальном значении x0 [a;b] , т. е. |
||||||||
lim xn+1 |
= limϕ (xn ) = c , f (c) = 0 , |
c [a;b]. |
||||||
n→∞ |
n→∞ |
|
|
|
||||
1 Постановка задачи. Определить количество действительных кор- |
||||||||
ней уравнения |
x3 + x2 −3 = 0 , |
|
||||||
|
|
|
|
|
(1) |
|||
отделить эти корни и, применив метод итераций, вычислить их с точностью ε =10−3 .
2 Отделение действительных корней уравнения (1) графическим методом (лабораторная работа № 3).
3 Вычисление действительного корня x [1; 1,5] методом итера-
ций с заданной точностью ε =10−3 . |
|
|
|
|
|
|
|
|
||||
Приведем уравнение (1) к виду |
|
|
|
|
|
|
|
|
||||
|
|
|
|
x = ϕ (x). |
|
|
|
|
|
(2) |
||
Есть много способов сведения уравнения (1) к виду (2), а именно: |
||||||||||||
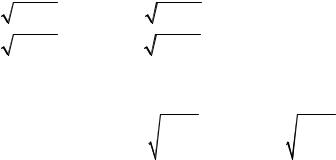
1) x = 3 3 − x2 , |
ϕ(x)= 3 3 − x2 ; |
|
|
|
|
|
|
|
|
|||
2) x = 3 − x3 , |
ϕ(x)= 3 − x3 ; |
|
|
|
|
|
|
|
|
|||
3) x (x2 + x)−3 = 0, x = |
|
3 |
, |
ϕ(x)= |
|
|
|
3 |
; |
|
||
x |
2 |
|
x |
2 |
|
+ x |
|
|||||
|
|
+ x |
|
|
|
|
|
|
|
|||
4) x2 (x +1)−3 = 0, x = |
|
3 |
, |
ϕ(x)= |
|
|
3 |
|
. |
|||
|
x +1 |
|
|
|
x + |
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|||
В случаях 2 и 4 выбрали положительные значения квадратного корня,
т. к. x [1; 1,5], т. е. x > 0 ;
