6.9 Анализ и интерпретация результатов моделирования

Цель любого эксперимента (натурного или расчетного) заключается в получении опытных данных об исследуемой системе. Опытные данные могут накапливаться либо с помощью активного эксперимента, либо с помощью пассивных наблюдений. В случае активного эксперимента воздействие на систему осуществляется по заранее спланированной программе – плану эксперимента.

В любом случае исследуемая система (объект) характеризуется:

а) входными параметрами x_i,i = 1 … n_i;

б) выходными параметрами y_j,j = 1 … n_j;

в) внутренними (собственными) параметрами h_k  H, k=1,n_k;

г) параметрами возмущающих воздействий v_l,l = 1 … n_l.

Параметры возмущающих воздействий оказывают влияние на систему и проявляют себя как случайные величины или случайные функции.

Одной из основных задач активного эксперимента является выявление взаимосвязей между входными и выходными параметрами системы и представление их в виде математической модели:

y = f(x₁, x₂, x₃). (6.8)

Входные параметры называют факторами. Каждый фактор имеет область определения (область допустимых значений). Комбинация факторов рассматривается как факторное пространство. Область возможных комбинаций факторов определяется планом эксперимента.

Факторы должны удовлетворять следующим требованиям:

а) управляемость;

б) однозначность (трудно управлять фактором, который в свою очередь является функцией других факторов);

в) независимость, т. е. возможность установки любого уровня фактора вне зависимости от уровней других факторов.

Математическая обработка результатов спланированного эксперимента позволяет получить уравнение регрессии, которое чаще представляется в виде полинома:

y = a₀ + ∑a_i∙x_i + ∑a_ij∙x_i∙x_j + ∑a_ii∙x_ii∙x²_i ,(6.9)

где a_i,a_ii,a_ijкоэффициенты регрессии.

Для правильного выбора степени полинома необходимо учитывать требования простоты и адекватности.

Проверка адекватности модели позволяет оценить совпадение результатов расчета по полученной модели с опытными данными. Такая проверка выполняется с помощью соответствующих критериев, например, F-критерия Фишера:

, (6.10)

где дисперсия адекватности;

 дисперсия, характеризующая ошибку опыта.

Модель считается адекватной, если значение F, полученное по формуле (6.10), не превышает соответствующего табличного значения при заданном уровне значимости.

6.9.1 Планирование эксперимента.Полным факторным экспериментом (ПФЭ) называется такой эксперимент, при реализации которого определяется значение функции отклика при всех возможных сочетаниях уровней варьируемых факторов. Если имеетсяkфакторов, каждый из которых может устанавливаться наqуровнях, то для осуществления ПФЭ необходимо поставитьn=q^kопытов. Если, например, используются два фактора, каждый из которых может устанавливаться на двух уровнях, то для реализации ПФЭ необходимо провести четыре опыта [8, 9].

Планирование, проведение и обработка результатов ПФЭ состоит из следующих обязательных этапов:

а) кодирование факторов;

б) составление плана-матрицы эксперимента;

в) реализация плана эксперимента;

г) проверка воспроизводимости параллельных опытов;

д) расчет коэффициентов регрессии линейной модели;

е) проверка адекватности линейной модели;

ж) оценка значимости коэффициентов регрессии.

Планирование эксперимента начинают с выбора влияющих факторов. В качестве таких факторов можно выбрать, например, интенсивность входного потока заявок или интенсивности потоков обслуживания заявок в первой либо во второй фазах системы (μ₁ или μ₂).

После выбора факторов для каждого из них необходимо установить нулевой уровень (среднее, исходное значение) r_ои интервал варьирования (r), а также верхний уровень фактораr_впутем прибавления к основному уровню интервала варьирования и его нижний уровеньr_нпутем вычитания интервала варьирования из основного уровня. Затем для того чтобы построить стандартную ортогональную матрицу планирования эксперимента необходимо перевести натуральные значения факторов в безразмерные величины, т. е. выполнить их кодирование, используя следующие формулы:

;

.

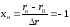Результаты кодирования факторов необходимо свести в таблицу 6.1.

Таблица 6.1 – Кодирование факторов

Наименование уровня фактора	Обозначение (кодир-е значения	Значение μ1	Значение μ2
Основной rо	0	2,5	3,0
Верхний rв	+1	4,0	3,5
Нижний rн	-1	1,0	2,5
Интервал варьирования (r)	Δ	1,5	0,5

После этого можно составить план-матрицу эксперимента (таблица 6.2). Строки этой таблицы соответствуют различным опытам, а столбцы 2 и 3 – значениям уровней факторов.

Таблица 6.2 - План-матрица эксперимента

Номер опыта	х1	х2	х1х2	yu1	yu2
1	2	3	4	5	6	7
1	+1	+1	+1
2	+1	–1	–1
3	–1	+1	–1
4	–1	–1	+1

Приведенную в таблице 6.2 матрицу называют расширенной матрицей эксперимента, т. к. в нее введен столбец 4, позволяющий оценить коэффициент регрессии при взаимодействии факторов x₁иx₂.

В процессе реализации плана эксперимента заполняются столбцы 5 и 6. Причем каждый опыт проводится как минимум два раза. В столбце 7 записываются вычисленные средние значения результатов двух серий эксперимента.

Далее необходимо проверить воспроизводимость параллельных опытов при одинаковом их числе на каждом сочетании уровней факторов по критерию Кохрена.

, (6.11)

где – дисперсия, характеризующая рассеяние результатов наu– м сочетании уровней факторов,;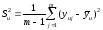

- среднее значение функции отклика вu-й строке матрицы планирования эксперимента,;

– наибольшая из дисперсийв строках плана;

_t(0,05;k₁;k₂)- табличное значение критерия Кохрена при пятипроцентном уровне значимости;

0,05 – уровень значимости (значение вероятности, отвечающее событиям, которые в данных условиях эксперимента можно считать практически невозможными);

k₁– число опытов в плане эксперимента,k₁ = n;

k₂– число степеней свободы каждой оценки,k₂ = m- 1;

m– число параллельных опытов.

Таблица значений критерия Кохрена приведена в приложении Б, а также в [3, 41].

Если проверка по критерию Кохрена (6.23) не выполняется, то следует обратить внимание на опыт с максимальным значением 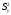и, возможно, повторить его. В случае воспроизводимости процесса переходят к расчету коэффициентов регрессии:

, (6.12)

, (6.13)

. (6.26)

После вычисления коэффициентов регрессии a_iнеобходимо проверить их значимость. Погрешность определения указанных коэффициентов оценивается дисперсией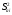. При этом дисперсии оценок всех коэффициентов регрессии одинаковы. Величиназависит только от дисперсии воспроизводимости экспериментаи числа опытов

. (6.14)

Проверка значимости коэффициентов регрессии выполняется с помощью t-критерия Стьюдента, расчетное значение которого

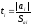. (6.15)

Полученное значение t_iдля каждого коэффициента регрессии сравнивается с табличнымt(0.05; k₁), определяемым при принятом уровне значимости и числе степеней свободыk₁, с которым определяется дисперсия воспроизводимости.

Если t_i<t(0.05; k₁), то коэффициентa_iнезначим и член уравнения регрессии, включающий этот коэффициент, исключается из математической модели.

Если же t_i>t(0.05; k₁), то коэффициентa_iзначим и его следует сохранить в регрессионной модели. В этом случае значение коэффициентаa_iбольше ошибки опыта, которую можно оценить величиной доверительного интервалаa_i, определяемого по формуле

a_i = t·S_ai. (6.16)

Таблица значений критерия Стьюдента приведена в приложении В.

Далее необходимо привести полученную линейную модель эксперимента в виде (6.20).

Следующим этапом работы является проверка адекватности полученной модели с помощью критерия Фишера. Модель считается адекватной, если имеет место неравенство

, (6.17)

где – дисперсия адекватности,;

y_pu– расчетное значение функции отклика вu-м опыте.

F(0,05; k₃; k₁) – табличное значении критерия Фишера при 5-процентном уровне зависимости;

k₃ – число степеней свободы дисперсии адекватности, k₃= n- k - 1.

Таблица значений критерия Фишера приведена в приложении Г.

Если после расчетов окажется, что условие (6.30) не выполняется, то это значит, что полученная модель не адекватно описывает реальный процесс. В таком случае, скорее всего, придется сузить интервалы варьирования факторов и весь процесс планирования эксперимента повторить.

Если же условие проверки по критерию Фишера выполнено, то полученная модель является адекватной и можно перейти к построению математической модели в натуральных единицах. Для этого необходимо подставить вместо x_iв полученное уравнение регрессии выражение, используемое при кодировании факторов. В результате преобразования получим модель в натуральных единицах, например в виде:

y = c_o + c₁·₂.(6.18)

6.9.2 Регрессионный анализ. Для проведения регрессионного анализа необходимо выполнение следующих условий:

а) результаты эксперимента y₁,y₂,…,y_n. представляют собой независимые, нормально распределенные случайные величины;

б) независимые переменные x₁,x₂,…,x_nизмеряются с пренебрежительно малой ошибкой по сравнению с ошибкой в определенииy₁;

в) при проведении эксперимента с объемом выборки Nпри условии, что каждый опыт повторенmраз, выборочные дисперсиидолжны быть однородны.

Для повышения достоверности исходных данных каждый опыт эксперимента необходимо провести несколько раз. Затем для каждой серии параллельных опытов вычислить средние значения результатов эксперимента каждого опыта и свести их в таблицу.

После этого следует построить график зависимости, например, вероятности отказа от интенсивности потока обслуживания второй фазы (рисунок 6.2, график 1).

На поле этого графика можно построить средствами пакета MSExcelлинию тренда (рисунок 6.2, график 2) и отобразить его уравнение, чтобы облегчить выбор аппроксимирующего выражения.

Далее необходимо дать оценку степени совпадения линии тренда и графика исходной зависимости. После чего можно отметить, что зависимость вероятности отказа от интенсивности потока обслуживания второй фазы носит, в данном случае, экспоненциальный характер.

1 – расчетный эксперимент; 2 – линия тренда; 3 – регрессионная модель

Рисунок 6.2 – Зависимость вероятности отказа от интенсивности потока обслуживания второй фазы и линия тренда

Рассмотрим пример построения регрессионной модели, используя эмпирическую зависимость вида

y = ae^bx. (6.19

Неизвестными в данной модели являются коэффициенты aиb. Для определения указанных неизвестных сначала прологарифмируем уравнение (6.19):

Ln(y) = Ln(a) + bxLn(e). (6.20)

Так как Ln(e) = 1, то выражение (6.20) можно записать в виде:

Ln(y) = Ln(a) + bx. (6.21)

Коэффициенты aиbнайдем с помощью метода наименьших квадратов при условии [7]

, (6.22)

где  y_ri– значение у, полученное в результате расчетного эксперимента;

n– количество экспериментальных данных – значенийx_iиy_i.

Подставим выражение (6.21) в (6.22) и получим:

 0. (6.23)

Введем обозначение Ln(a) = с, тогда

0. (6.24)

Найдем частные производные от выражения (6.24) по си поbи приравняем их к нулю. Получим систему из двух уравнений:

(6.25)

Подставим в систему (6.25) численные значения соответствующих сумм, рассчитанных в исходной таблице. Расчеты можно выполнить с помощью программы MSExcel. В результате получим следующую систему линейных алгебраических уравнений:

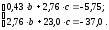(6.26)

Для решения системы (6.26) можно воспользоваться математическими функциями МОБРиМУМНОЖмастера функций программыMSExcel, программойMathCadили другими доступными программными средствами.

Систему уравнений (6.39) можно решить также с помощью команды "Сервис, Поиск решения" программы Excel, а также в среде программMatLab,MathCadи т. др.

Решение системы (6.39): b = -13,259;с = -0,0176.

Так как с = Ln(a), тоа = е^с = е^-0,0176 = 0,983.

Таким образом, получаем уравнение

y = 0,983 e ^{–13.259x}.(6.27)

При использовании функций МОБРиМУМНОЖпрограммыExcelследует иметь в виду, что перед вызовом данных функций необходимо выделить блок ячеек результата, затем ввести в соответствующие поля окна мастера функции блоки ячеек исходных матриц и нажать клавишуEnter, удерживая нажатыми клавишиCtrlиShift.

На рисунке 6.2 график 3, построенный по полученному уравнению регрессии (6.27), полностью совпал с линией тренда, построенной с помощью программы MSExcel.