Элементы математической логики.

Математическая логика – разновидность формаьной логики, т.е. науки, которая изучает умозаключения с точки зрения их формального строения.

Определение. Высказыванием называется предложение, к которому возможно применить понятия истинно или ложно.

В математической логике не рассматривается сам смысл высказываний, определяется только его истинность или ложность, что принято обозначать соответственно И или Л.

Понятно, что истинные и ложные высказывания образуют соответствующие множества. С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами “и”, “или”.

Таким образом, операции с высказываниями можно описывать с помощью некоторого математического аппарата.

Вводятся следующие логические операции (связки) над высказываниями

1. Отрицание. Отрицанием высказывания Р называется высказывание, которое истинно только тогда, когда высказывание Р ложно.

Обозначается Р или.

Соответствие между высказываниями определяется таблицами истинности. В нашем случае эта таблица имеет вид:

P	Р
И	Л
Л	И

2) Конъюнкция. Конъюнкцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания.

Обозначается P&Q или РQ.

P	Q	P&Q
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

3) Дизъюнкция. Дизъюнкцией двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны.

Обозначается PQ.

P	Q	PQ
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

4) Импликация. Импликацией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда высказывание Р истинно, а Q – ложно.

Обозначается PQ (или РQ). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.

P	Q	PQ
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

5) Эквиваленция. Эквиваленцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают.

Обозначается РQ или РQ.

P	Q	PQ
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

С помощью этих основных таблиц истинности можно составлять таблицы истинности сложных формул.

Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы  и .

Составим таблицы истинности для каждой формулы:

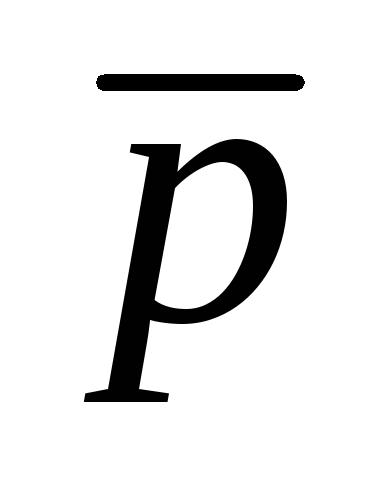
p	r		(pr)
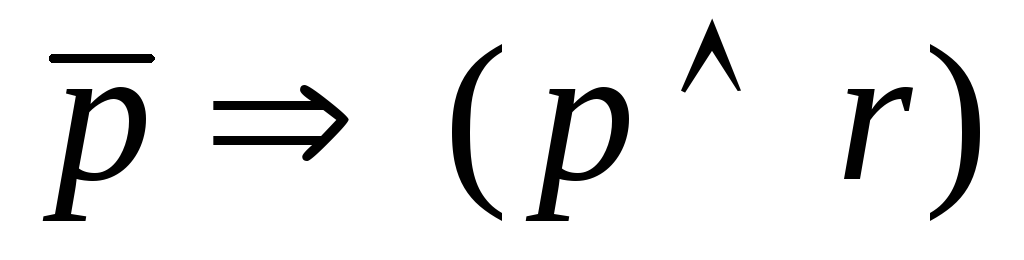
И	И	Л	И	И
И	Л	Л	Л	И
Л	И	И	Л	Л
Л	Л	И	Л	Л

p	r
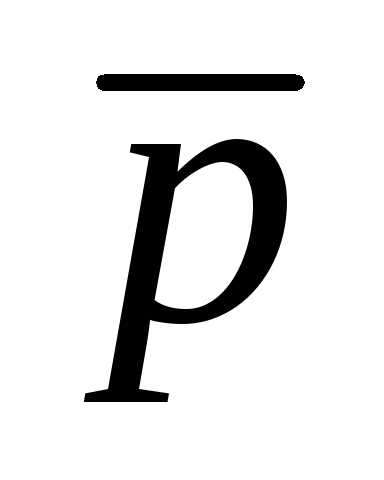
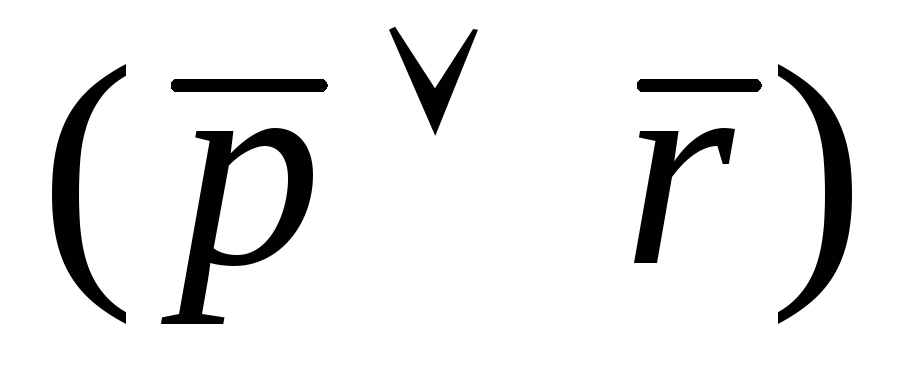
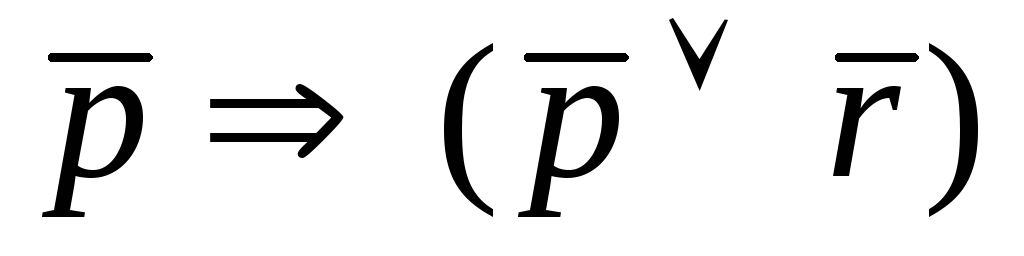
И	И	Л	Л	Л	И
И	Л	Л	И	И	И
Л	И	И	Л	И	И
Л	Л	И	И	И	И

Данные формулы не являются эквивалентными.

Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы  и .

Составим таблицы истинности для заданных формул.

p	q	r	pq	(pq)r
И	И	И	И	И
И	И	Л	И	И
И	Л	И	Л	И
И	Л	Л	Л	Л
Л	И	И	Л	И
Л	И	Л	Л	Л
Л	Л	И	И	И
Л	Л	Л	И	И

p	q	r	pq	qp	(pq)(qp)	(pq)(qp)r
И	И	И	И	И	И	И
И	И	Л	И	И	И	И
И	Л	И	Л	И	И	И
И	Л	Л	Л	И	И	И
Л	И	И	И	Л	И	И
Л	И	Л	И	Л	И	И
Л	Л	И	И	И	И	И
Л	Л	Л	И	И	И	И

Из составленных таблиц видно, что данные формулы не равносильны.

100