4. ЧИСЛЕННЫЕ МЕТОДЫ ПОИСКА ЭКСТРЕМУМОВ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Во многих инженерных задачах интерес представляют не только нули функции (задача нахождения корней уравнения) но и другие важные для практического использования точки. Речь идет об экстремумах функции, т.е. о максимальных и минимальных значениях. Задачи такого рода довольно часто встречаются на практике.

Рассмотрим методы нахождения экстремумов функций одно переменной. Мы будем рассматривать функцию f(X), непрерывную на [a;b].

Будем считать, что x* [a; b] является точкой минимума функции f(x), если

f(x*) ≤ f(x) для всех x [a; b]

или точкой максимума, если

f(x*) ≥ f(x) для всех x [a; b].

Задача заключается в том, чтобы найти точку х* и значение f(x*), удовлетворяющую выше приведенным условиям.

В математическом анализе подобная задача решается с использованием аппарата дифференциального исчисления. В этом случае находят все точки подозрительные на экстремум. Некоторые из таких точек определяются из условия равенства нулю первой производной исследуемой функции. Однако на практике применение таких методов довольно ограничено. Поэтому для поиска экстремума функции применяют численные методы. Конечно, и в этом случае иногда возникают трудности. Это связано прежде всего с априорной неизвестностью характера кривых, являющихся графиками исследуемых функций. Поэтому в общем случае нельзя сказать, сколько экстремумов имеет функция на заданном интервале. Большинство численных методов поиска экстремума не дают ответа на этот вопрос, а найденный с их помощью экстремум может оказаться локальным. Но поскольку наша задача рассмотреть использование Microsoft Excel как инструмента для решения некоторых типовых задач, ограничимся рассмотрением унимодальных функций, т.е. таких функций, которые имеют единственный экстремум на исследуемом отрезке [a;b].

Постановказадачи

Найти экстремум функции y=f(x), x е [a; b] с точностью e .

Инструменты MS Excel

Формулы, встроенные функции (категория математические), Поискрешения.

Поиск решения

Поиск решения позволяет:

-находить заданное, минимальное или максимальное значение целевой функции;

-находить значения одного или несколькихаргументов;

-накладывать ограничения на аргументы, обеспечивая этим достаточно точное

решение.

С помощью функции поиска решения можно вести поиск оптимального или фиксированного значения исследуемой функции в “целевой” ячейке, изменяя до 200 переменных (ячеек). При этом для каждой переменной можно задать ограничения, например, верхнюю или нижнюю границу. Прежде чем запустить поиск решения, необходимо сформулировать математическую модель. Целевые ячейки должны

11

содержать формулу, которая ссылается на изменяемые ячейки. Значения в измененных ячейках будут последовательно изменяться до тех пор, пока не будет получено нужное значение в целевой ячейке.

Решение задачи выполняется в дваэтапа:

1.отделение точки экстремума, т.е. определение начального приближенияс;

2.уточнение экстремума функции с использованием Поиска решения.

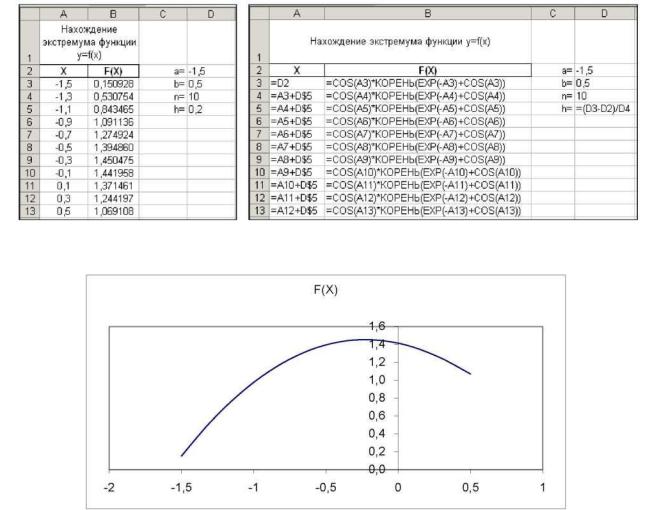
Пример 3. Найти экстремум функции на заданном интервале, с точностью0,0001: f (x) = cos xex + cos x; x e[-1,5; 0,5]

Последовательность действий Отделение точки экстремумауравнения.

1.Выполнить табулирование функции.

2. Построить график функции.

По графику видно, что на заданном интервале функция имеет локальный максимум. Из таблицы видно, что начальным приближением точки экстремума можно взять значение -0,3.

Уточнение экстремума функции Для уточнения результата с помощью инструмента Поиск решения в электронную

таблицу ввести значения с и f(c). Для этого:

1.в ячейки E2 и F2 ввести текст C и F(C);

2.в ячейку E3: -0,3;

3.в ячейку F3 скопировать формулу из ячейки B3;

12

4.выполнить команду Поиск решения;

5.в диалоговом окне Поискрешения:

-в поле Установить целевую ячейку ввести ссылку на ячейку$F$3

-в группе Равной: выбрать переключатель максимальномузначению;

-в поле Изменяя ячейки ввести ссылку на ячейку$E$3;

-нажать кнопку Параметры

-диалоговом окне Параметры в поле Относительная погрешность установить значение 0,0001. НажатьOK;

5.ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Наиболее употребительными приближенными методами вычисления определен-

ных интегралов являются метод прямоугольников и метод трапеций, которые получают исходя из геометрического смысла интеграла как площадикриволинейной

13

трапеции. Основная идея этих методов заключается в замене подынтегральной функции f(x) многочленом, совпадающим с f(x) в некоторых точках. Функция f(x) предполагается непрерывной на [a, b]. Очевидно, что точность вычислений зависит от числа отрезков, на которые разбивают промежутокинтегрирования.

Формула прямоугольников имеет вид:

где xk =a+kh; k=0,1…,n; h=(b–a)/n; ξk [xk-1, xk].

Суть метода заключается в том, что на каждом из отрезков [xk-1, xk] площадь криволинейной трапеции, ограниченной графиком f(x), заменяется площадью прямо-

угольника со сторонами h и f (ξk). Различают формулы:

а) левых прямоугольников, когда ξ =x0 (рис.1),

yk

y0 yn

∫a f (x)dx =h(y0 +y1 +...+yn−1)+Rn , yk = f(xk ), b) правых прямоугольников, когда ξk= xk (рис.2).

yk

y1 yn

Рис. 2.

14

b

∫a f(x)dx =h(y1 +y2 +...+yn )+Rn, yk = f(xk ),

Формула трапеции имеет следующийвид:

где

y1

yn yn

y0

Рис. 3.

Геометрически это означает, что криволинейная трапеция (при f(х)≥0), площадь которой численно равна интегралу, приближенно заменяется фигурой, ограниченной сверху ломаной, соединяющей точки с координатами (xk, f(xk)) и (xk-1, f(xk- 1)), k=1, 2, …, n.

Определенную сложность представляет оценка Rn. Поэтому при вычислении интегралов по формулам прямоугольников и трапеций погрешность определяют как абсолютную величину разности значений интегралов, вычисленных при n и 2n разбиениях промежутка интегрирования, т.е.

Rn=|I2n–In|.

Вычислив интеграл при n=10, возьмем n=20 и снова рассчитаем тот же интеграл.

моугольников, формуле трапеции с точность до 0,001. Для оценки точности использовать просчет при n=10, n=20 и т.д. (Rn=|I2n-In|).

15

Технологиявыполнения:

1. Выполним табулирование подинтегральнойфункции f (x) = tg(x2 +0,5) на отрезке

1+ 2x2

x [0,4; 0,8], приn=10.

2. Введем поясняющие надписи в ячейки D6:D8.

3.В ячейку E6 введем формулу для вычисления определенного интеграла методом левых прямоугольников: =E5*СУММ(B3:B12). В ячейку E7 введем формулу правых прямоугольников: =E5*СУММ(B4:B13). В ячейку Е8 введем формулу трапеции: =E5*((B3+B13)/2+СУММ(B4:B12))

4.Для сохранения результата и расчета погрешности вычислений выполним следующие действия.

Вячейки G2, H2, I2 введите поясняющий текст. В ячейку G3 введите число разби-

ений отрезка x [0,4; 0,8] , в нашем случае это 10. В ячейку H3 скопируйте из ячей-

ки Е8 рассчитанное значение определенного интеграла по формуле трапеции. В ячейке Н3 должно быть значение, а не формула. Для вставки значения в ячейку Н3 нужно использовать команду Специальная вставка и в окне диалога Специальная вставка установить переключательзначение.

16

Результат представлен в ячейках G3:H3.

5. Вычислим определенный интеграл по формулам левых и правых прямоугольников и формуле трапеции при n=20. Заменим n=10 на 20. Скопируем формулы из диапазона ячеек A13:B13 в диапазон A13:B23. Изменим формулы левых, правых прямоугольников и формулу трапеции, в соответствии с дополнением основной таблицы.

17

6. В ячейках G4 и H4 аналогично сохраним результат вычисления интеграла по формуле трапеции при n=20.

В ячейку I4 введите формулу для определения точности расчета =ABS(Н4-Н3).

Для вычисления интеграла с заданной точностью такой перерасчет и сохранение результата выполняют до тех пор, пока Rn не станет меньшим или равным ε .

3. ПРОГРАММИРОВАНИЕ ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИЯЗАДАЧ

Вычисление определенныхинтегралов

Определенный интеграл ∫ ( ) выражает площадь криволинейной трапе-

ции - фигуры ограниченной отрезком [а;b] оси OX, прямыми, проходящими через точки x=a и х=b оси OY, и графиком функции f(x).

Геометрический смысл интеграла лежит в основе простейших методов вычисления определенного интеграла - левых прямоугольников, правых прямоугольников и трапеции.

Разобьем отрезок [а;b] на n равных частей точками х0=а, xj, xn и проведем через них прямые параллельные оси OY. Заменим верхнюю криволинейную границу каждой частичной трапеции отрезком прямой, параллельной оси OX. Получим ступенчатую фигуру, площадь которой приближенно равна площади криволинейной трапеции и, следовательно, интегралу. Определив площадь каждого прямоугольника и просуммировав площади получим формулы для приближенного вычисления интеграла.

Формула левых прямоугольников

Формула правых прямоугольников

18

Формула трапеции

Методы вычисления определенного интеграла сводятся к табулированию подинтегральной функции и суммированию полученных значений.

По приведенным выше формулам интеграл вычисляется приближенно. Недостатком формул является то, что величина погрешности остается неизвестной. В вычислительной математике выводятся формулы для оценки погрешности приближенных методов интегрирования. Однако эти формулы громоздки и неудобны в практических расчетах. Воспользуемся следующим приемом оценки точности вычислений. После вычисления интеграла при n=10, возьмем n=20 и снова рассчитаем тот же интеграл. Если первый раз получилось значение I1, а второй раз I2

и если |I2–I1| < ε , то считается, что заданная степень точности ε достигнута. Если же |I2–I1| >ε, то принимают n=40 и снова рассчитываютинтеграл.

19