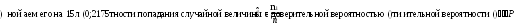Курсовая работа / Вариант 8 - Браженков - Марченко - 2004 / вар8

Российский Химико-Технологический университет им. Д.И. Менделеева

Кафедра стандартизации и сертификации

Статистическая обработка экспериментальных данных при сертификации продукции

Оценивание распределений их параметров

Выполнила: студентка гр. К-53

Марченко Т.Н. (вариант №8)

Проверил: Браженков Андрей

Игоревич

Москва 2004

Задание.

В ста случаях зарегистрировано время (в сек) обнаружения цели оператором радиолокационной станции с момента её появления в зоне РЛ.

13,5	25,5	53,5	10,5	10	23	17,5	13,5	3	12,5
8	59	1,5	1,5	0	27	42,5	15	19,5	21,5
7,5	29,5	1,5	71,5	35	5	41	35,5	32	33,5
8,5	14,5	21,5	142,5	1,5	8,5	92,5	21	13	1,5
44	11	15,5	3	12,5	0	14,5	85	121	11
15,5	39,5	58,5	0	50,5	27,5	16	19	6,5	8
21	158	0	16	26	51	3,5	31,5	12	34
33,5	14,5	8,5	2	10,5	48	56	45,5	13	4,5
83,5	3,5	29	66	10,5	10	14	0	2,5	13
10	29	32,5	48	9,5	21	49,5	15	39,5	32,5

1. Найти оценки математического ожидания и дисперсии случайной величины Х.

2. Найти доверительные интервалы для математического ожидания и дисперсии, соответствующие заданной доверительной вероятности ((1 - α) = 0,85).

3. Оценить вероятность попадания случайной величины Х в заданный интервал (0,8 ÷ 1,1)x_ср .

4. Для этой вероятности найти доверительный интервал, соответствующий заданной доверительной вероятности ((1 - α) = 0,80).

5. Построить гистограмму и эмпирическую функцию распределения случайной величины Х.

6. Найти и построить доверительные области для плотности распределения f (x) и функции распределения F (x), соответствующие заданной доверительной вероятностью ((1 - α) = 0,85) для f(x) и ((1 - α) = 0,90) для F(x)

7. Сгладить гистограмму и эмпирическую функцию распределения подходящим законом распределения.

8. Используя критерий согласия χ² и критерий Колмогорова, проверить правдоподобие гипотезы о совпадении выбранного закона распределения с истинным законом распределения при заданном уровне значимости ( α = 0,01).

Решение.

Располагаем экспериментальные данные в порядке возрастания:

0	2	8	10,5	13,5	16	23	32,5	42,5	58,5
0	2,5	8	10,5	13,5	16	25,5	32,5	44	59
0	3	8,5	11	14	17,5	26	33,5	45,5	66
0	3	8,5	11	14,5	19	27	33,5	48	71,5
0	3,5	8,5	12	14,5	19,5	27,5	34	48	83,5
1,5	3,5	9,5	12,5	14,5	21	29	35	49,5	85
1,5	4,5	10	12,5	15	21	29	35,5	50,5	92,5
1,5	5	10	13	15	21	29,5	39,5	51	121
1,5	6,5	10	13	15,5	21,5	31,5	39,5	53,5	142,5
1,5	7,5	10,5	13	15,5	21,5	32	41	56	158

1. Находим точечные оценки математического ожидания и дисперсии, учитывая, что n = 100, по формулам:

- для математического ожидания MX - выборочное среднее:

-для дисперсии DX – исправленная дисперсия:

- выборочная дисперсия – DX

2. Находим доверительные интервалы для математического ожидания и дисперсии для доверительной вероятности (1 - α) = 0,85.

1) 2Φ(ε_α) = 1 – α, Φ(ε_α) – функция Лапласа

Φ(ε_α) = (1 - α)/2 = 0,85/2=0,425

По таблице для функции Лапласа находим ε_α = 1,44

2) а) доверительный интервал для математического ожидания:

Mx1 = 26,61 – 1,44ּ Mx2 = 26,61 +1,44ּ

M_x1≤M_x≤M_x2, 22,4818≤26,61≤30,7382

б) доверительный интервал для дисперсии:

Dx1 = = 679,4575 Dx2= = 1025,69609

D_x1≤D_x≤D_x2, 679,4575≤821,8565≤1025,69609

3. Вероятность попадания случайной величины Х в заданный интервал (0,8 ÷1,1) 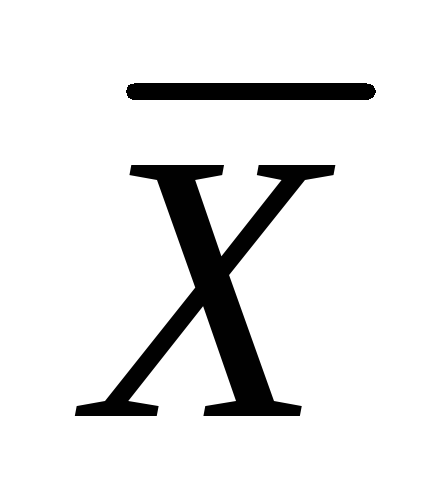, то есть 21,288 ≤ ≤ 29,271:

, m = 9 – число значений, попавшее в данный интервал,

n = 100 – общее число значений

4. Доверительный интервал для вероятности попадания случайной величины с доверительной вероятностью (1 - α) = 0,80:

2Φ(ε_α) = 1 – α, Φ(ε_α) – функция Лапласа

Φ(ε_α) = (1 - α)/2 = 0,80/2=0,40

По таблице для функции Лапласа находим ε_α = 1,28

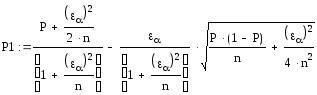
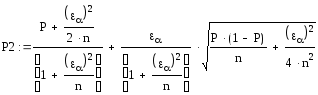
Р1 = 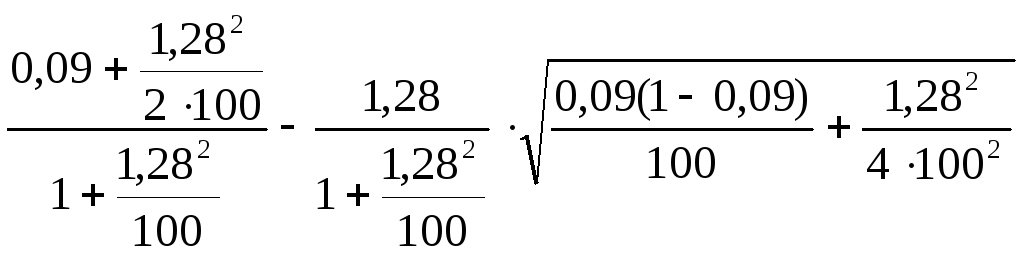=0,059678

Р2 = 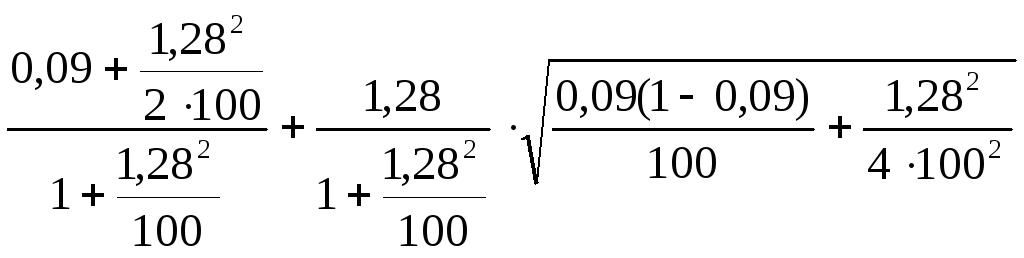=0,1335401

P_x1≤P_x≤P_x2, 0,059678≤0,09≤0,1335401

5. 1) Для построения гистограммы Г(x) заключаем все экспериментальные данные в интервал (0;160) и разбиваем его на 10 равных разрядов.

Значение гистограммы Г(x) находим по формуле : ,

где - число экспериментальных точек, попавших в этот разряд ;

- его длина.

_{величина интервала:}

_{количество разрядов: k = 1}

величина разряда:

№разряда	Разряд		Частота попадания случайной величины X в разряд		Значение гистограммы Г (х)
	нижняя граница	верхняя граница
			ni
1	0	15,8	50	0,5	0,031646
2	15,8	31,6	19	0,19	0,012025
3	31,6	47,4	14	0,14	0,008861
4	47,4	63,2	9	0,09	0,005696
5	63,2	79	2	0,02	0,001266
6	79	94,8	3	0,03	0,001899
7	94,8	110,6	0	0	0
8	110,6	126,4	1	0,01	0,000633
9	126,4	142,5	1	0,01	0,000633
10	142,5	158	1	0,01	0,000633

Гистограмма представлена на рисунке 1.

_{Рисунок 1}

_.

_{2) Построение эмпирической функции распределения случайной величины.}

Соответствующую эмпирическую функцию рассчитываем по формуле:

,

где - число экспериментальных точек, лежащих левее Х.

график F(x) представлен на рисунке 2 _{Рисунок 2}

6. Построение доверительных областей для плотности распределения f (x) и функции распределения F (x), соответствующие заданной доверительной вероятности (1 - α) = 0,85 и (1 - α) = 0,90.

1) Построение доверительной области для функции распределения F (x):

- (1 - α) = 0,90  по таблице Колмогорова  = 1,23

- максимальное расхождение D истинной функции распределения и эмпирической функции: D =

- искомая область выражается следующим образом:

 F (x) 

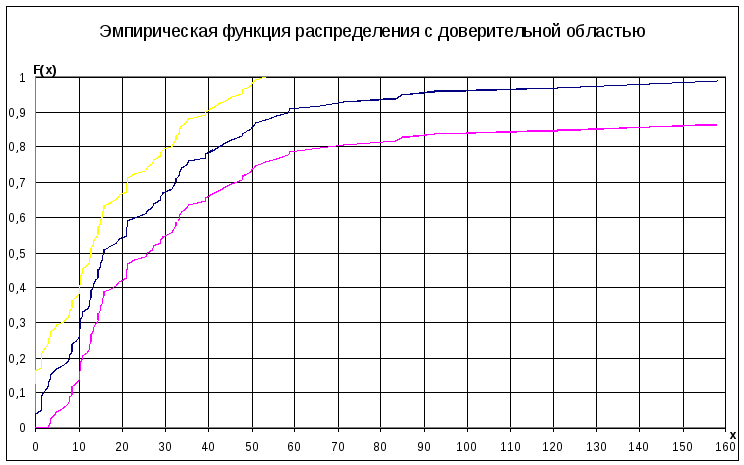
Таблицу доверительных границ для F(x) см. в приложении

Функция распределения является вероятностью, следовательно, доверительная область для нее не может распространяться ниже нуля и выше единицы.

График эмпирической функции распределения F(x) с доверительной областью.

Рисунок 3.

2) Построение доверительной области для плотности распределения f (x):

- для каждого разряда находим частоту попадания случайной величины Х

, где n_i – число экспериментальных точек, попавших в i-ый разряд

Это было определено в 5 пункте.

- находим доверительную вероятность (1-α₁) для построения доверительной области на каждом разряде:

(1-α₁) = 1 – α/r, r = 11 – число разрядов, включая полубесконечные.

(1-α₁) = 1 – 0,15/11 = 0,9864  α₁ = 0,15

- находим величину ε_α из условия: 2Φ(ε_α) = 1 – α₁, Φ(ε_α) – функция Лапласа

Φ(ε_α) = (1 – α₁)/2 = 0,9864/2=0,4932

По таблице для функции Лапласа находим ε_α = 2,5

- для каждого разряда гистограммы находим доверительную область для вероятности попадания случайной величины в этот разряд по формулам:

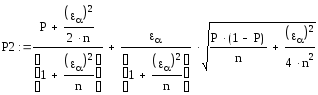
- для каждого разряда гистограммы находим доверительную область для плотности распределения: и (для полубесконечных разрядов считаем, что они лежат в доверительной области )

Рассчитываем и строим следующую таблицу.

Разряд(Xi-1,Xi)	Частота попадания случайной величины X в разряд (Xi-1,Xi)	Доверительная область для вероятности попадания случайной величины в разряд (Xi-1,Xi)		Доверительные границы для плотности распределения f (x)
0
15,8	0,5	0,378732	0,6212678	0,02397	0,039321
31,6	0,19	0,111357	0,3051139	0,007048	0,019311
47,4	0,14	0,074396	0,2479566	0,004709	0,015693
63,2	0,09	0,040638	0,1875976	0,002572	0,011873
79	0,02	0,004075	0,0923961	0,000258	0,005848
94,8	0,03	0,007886	0,1074077	0,000499	0,006798
110,6	0	0	0,0588235	0	0,003723
126,4	0,01	0,001232	0,0764154	7,8E-05	0,004836
142,2	0,01	0,001232	0,0764154	7,8E-05	0,004836
158	0,01	0,001232	0,0764154	7,8E-05	0,004836

Гистограмма с доверительной областью изображена на рисунке 4.

Рисунок 4.

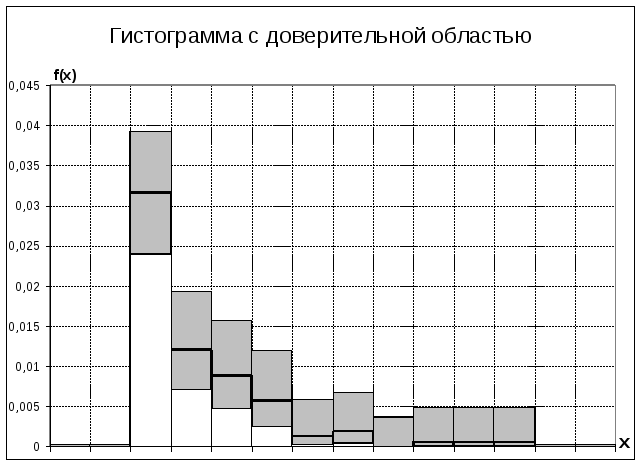
7. Сглаживание гистограммы и эмпирической функции распределения подходящим законом распределения.

Из формы гистограммы следует, что гипотетическим распределением может быть экспоненциальное распределение с функцией

,

.

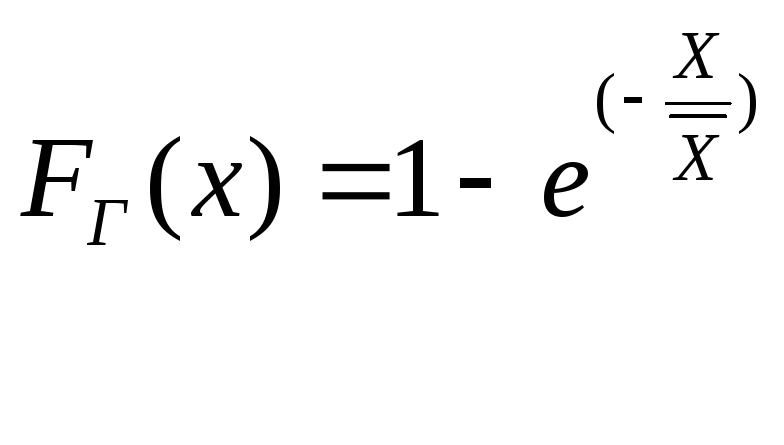Определим F_г(Х) для нескольких Х, полученные результаты занесем в таблицу.

x	Fг	x	F(x)
-7,9	-0,345654985	0	0
7,9	0,256867465	0	0,01
23,7	0,589608056	0	0,02
39,5	0,773362705	0	0,03
55,3	0,874840468	0	0,04
71,1	0,930881154	1,5	0,05
86,9	0,961829396	1,5	0,06
102,7	0,978920438	1,5	0,07
118,5	0,988358897	1,5	0,08
134,3	0,993571248	1,5	0,09
150,1	0,996449748	2	0,1
165,9	0,998039387	2,5	0,11

Эмпирическая F(x) и гипотетическая F_г(x) функции распределения

Рисунок 5

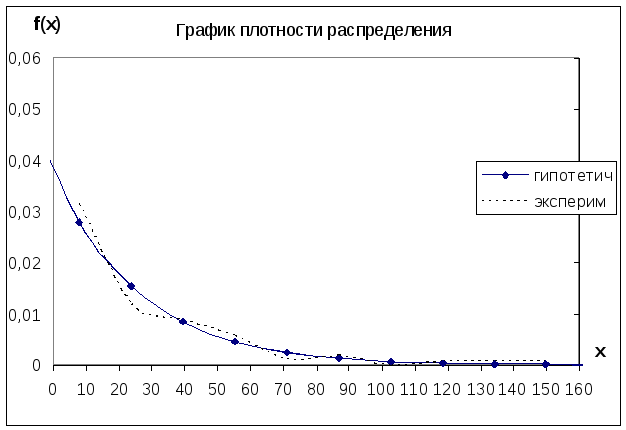
Для плотности распределения:

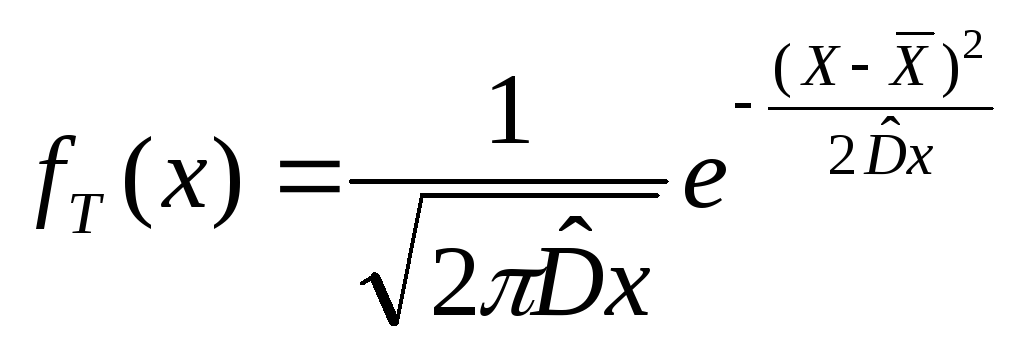
Значение f_г(x) при разных значениях Х.

x	fг	fэ
-7,9	0,050569522
7,9	0,027926815	0,03164557
23,7	0,015422471	0,012025316
39,5	0,008516997	0,008860759
55,3	0,004703477	0,005696203
71,1	0,002597476	0,001265823
86,9	0,001434446	0,001898734
102,7	0,000792167	0
118,5	0,000437471	0,000632911
134,3	0,000241592	0,000632911
150,1	0,000133418	0,000632911
165,9	7,36795E-05

График для плотности распределения представлен на рисунке 6.

Рисунок 6

7. Проверка правдоподобия гипотезы о совпадении выбранного закона распределения с истинным законом при уровне значимости α = 0,01.

1) Для проверки гипотезы с уровнем значимости 1 используем критерий Пирсона . Экспериментальное значение находим по формуле:

,

где - число разрядов гистограммы (включая полубесконечные разряды),