5. Сущность средних взвешенных арифметических и гармонических индексов.
Осн формой общ индексов явл агрегатный индекс, который представляет собой отношение агрегатов, т.е. соединений различных (однородных и неоднородных) элементов сложного показателя, приведенного к сопоставимому виду. Числитель этого индекса расчитывают как сумму произведений индексируемой величины отчетного периода на веса (соизмерители). Знаменатель агрегатного индекса находят как сумму произведений индексируемой величины базисного периода на те же веса (соизмерители).
Выбор формы агрегатного индекса непосредственно зависит от наличия исходной информации. Для расчета общего индекса физического объема товаров стандартную формулу обычно записывают так:
В свою очередь общий индекс цен на товары выглядит следующим образом:
Однако в ряде случаев станд формулы общ индексов могут б преобразованы в сред арифм или средние гармонические индексы.
средний арифметическийиндексфизического объема:
Если в стандартную формулу вместо q0подставить
то получимсредний гармоническийиндекс физического объема:
.
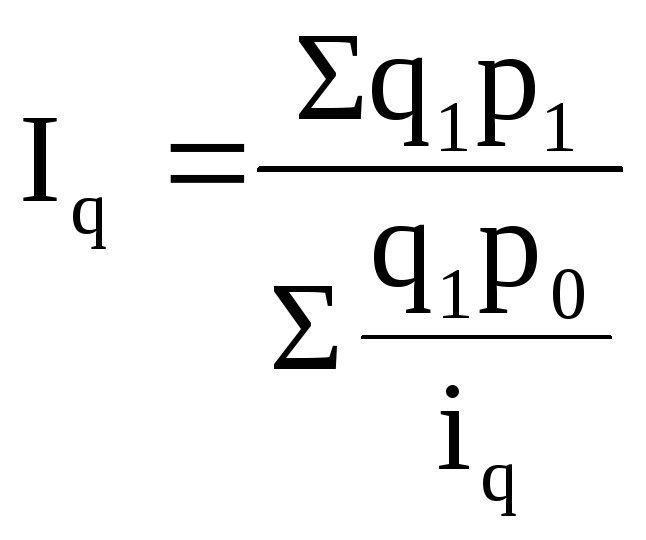6. Сущность средней как статистического показателя. Средняя арифметическая, область ее применения.
Средняя величина – это обобщенная колич характеристика признака в стат совокупности. Она выражает типичное значение признака для всех единиц совокупности под влиянием всего комплекса факторов.
Средняя величина явл важнейшей категорией стат науки и важнейшей формой обобщающих показателей. Осн условием правильного прим средних величин является качественная однородность стат совокупности. Среднее, вычисленные для качественно неоднородной совокупности, теряют свое научное значение. Такие средние являются фиктивными
Средняя арифметическая простая величина:
,
где n – число единиц в статистической совокупности.
Средняя арифметическая величина взвешенная величина определяется по формуле:
.
где f – локальные частоты (частости).
7. Основные виды и формы средних величин, область их применения.
Cред хронологическая величина.
Среднюю величину, исчисленную в разные моменты или за различные периоды времени, принято называть средней хронологической. Её применяют для нахождения среднего уровня в динамических рядах.
где
-
порядковые уровни моментного ряда; n –
число моментов ряду.
В тех случаях, когда необходимо определить средний уровень моментного ряда динамики с неравными промежутками между моментами, обычно используют формулу средней арифметической взвешенной величины.
Средняя квадратическая величина.
где х – варианты ранжированного ряда; n – общее число вариант.
средняя геометрическая величина.
где П – знак произведения; х – варианты; n – общее число вариант в ранжированном ряду.
Для дискретного или интервального ряда средняя геометрическая рассчитывается по взвешенной форме:
где f – частота дискретного или интервального ряда.
Средняя
гармоническая величина.
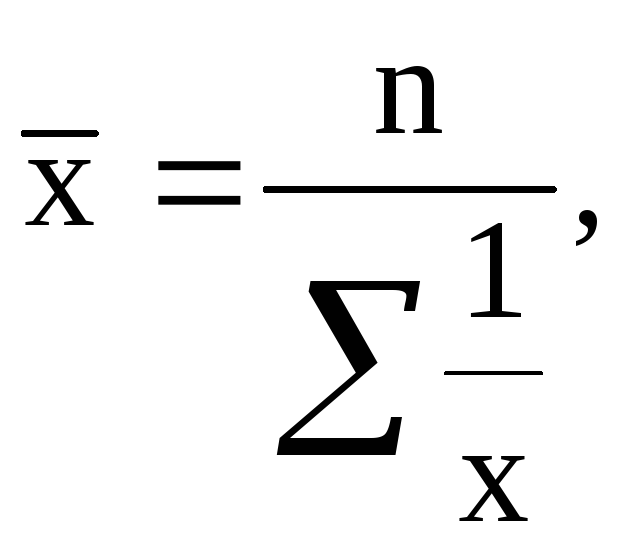
где
n
– общая численность вариант;
- обратное значение варианты.
средняя гармоническая взвешенная величина:
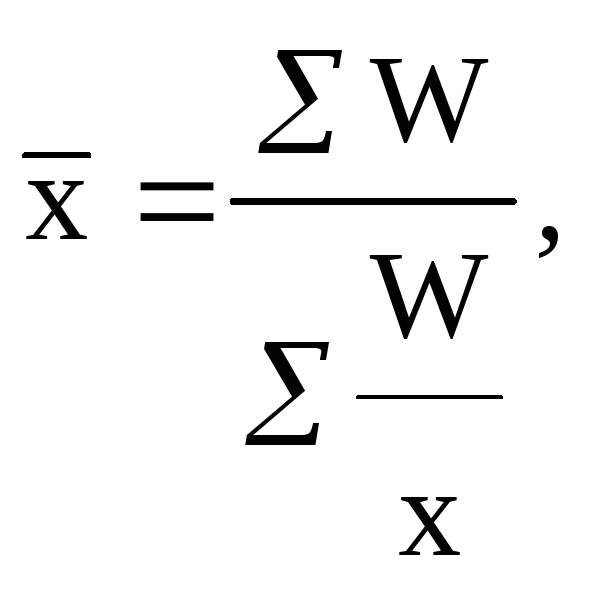
где W – произведение варианты на частоту (взвешенная варианта, xf).