

91
Програма-функція формування з довільного вектора Z, що має m елементів, нового вектора, який складається з непарних елементів вектора Z:
Для формування вектора U звертаємося до програми-функції Vector:
Результати обчислень:
Програма-функція обчислення суми елементів довільного вектора Z:

92
Для отримання суми елементів сформованого вектора U звертаємося до програми-функції Sum:
Суму елементів вектора U можна обчислити також так:
Пояснення до набору програми-функції Vector:
1.Друкуємо Vector(m, Z):= та натискаємо тричі кнопку  . З'явиться вертикальний стовпчик з полями введення.
. З'явиться вертикальний стовпчик з полями введення.
2.Задаємо початкове значення змінної k, що входить до циклу. Ця частина програми виконується один раз.
3.Для запису циклу типу for необхідно:
Натиснути кнопку  на палітрі засобів програмування. З'явиться оператор for з трьома полями для введення.
на палітрі засобів програмування. З'явиться оператор for з трьома полями для введення.
В поле ліворуч від символу надрукувати ім'я параметру циклу (i), а в поле
праворуч від символу ввести діапазон зміни параметру циклу 1..m.
В полі введення, яке залишилося, натиснемо кнопку  . З'явиться два поля для введення операторів.
. З'явиться два поля для введення операторів.
|
|
|
Z |
i |
|
|
В першому полі введення друкуємо L Zi |
2 floor |
|
. |
|
|
|
||||
|
|
|
2 |
||
В другому полі введення натиснемо кнопку  на палітрі засобів програ-
на палітрі засобів програ-
мування. В праве поле оператора if введемо логічний вираз L 1 (L дорівнює одиниці, якщо елемент непарний). В лівому полі натиснемо кнопку
1 (L дорівнює одиниці, якщо елемент непарний). В лівому полі натиснемо кнопку  . З'явиться два поля для введення операторів.
. З'явиться два поля для введення операторів.
В першому полі рахуємо кількість непарних елементів k k 1.
В другому полі формуємо вектор W із непарних елементів вектора Z:
Wk Zi.
4. Для отримання значень натисніть в полі першого вертикального стовпчика
кнопку  на палітрі матричних і векторних операцій. З’явиться діалогове вікно Insert Matrix (Вставить матрицу). В поле Rows (рядки) введіть значення - "2", в поле Columns (стовпчики) - "1" і натисніть OK. Mathcad утворить вектор з порожніми полями для заповнення. В першому полі друкуємо "k", другому - "W".
на палітрі матричних і векторних операцій. З’явиться діалогове вікно Insert Matrix (Вставить матрицу). В поле Rows (рядки) введіть значення - "2", в поле Columns (стовпчики) - "1" і натисніть OK. Mathcad утворить вектор з порожніми полями для заповнення. В першому полі друкуємо "k", другому - "W".
Пояснення до набору програми-функції Sum:
1.Друкуємо Sum(m,Z):= та натискаємо кнопку  . З'явиться вертикальний стовпчик з двома полями введення.
. З'явиться вертикальний стовпчик з двома полями введення.
2.Задаємо початкове значення змінної S, що входить до циклу. Ця частина програми виконується один раз.
3.Для запису циклу типу for необхідно:

93
Натиснути кнопку  на палітрі засобів програмування. З'явиться оператор for з трьома полями для введення.
на палітрі засобів програмування. З'явиться оператор for з трьома полями для введення.
В поле ліворуч від символу надрукувати ім'я параметру циклу ''i'', а в поле
праворуч від символу ввести діапазон зміни параметру циклу 1..m.
В полі введення, яке залишилося, обчислюємо суму непарних елементів
S S+Zi.
Значення суми обчислюється через ім’я програми-функції Sum. Зауваження: В прикладах, що наведені далі, пояснень до набору програм-
функцій не буде.
Приклад 2. Серед елементів масиву Z ={10; 3; 0; -5; 13; 8; -4; } визначити значення першого від'ємного елемента та його номер.
Реалізація завдання.
Введення початкових даних:
Програма-функція визначення номера першого від’ємного елемента будьякого вектора W:
Для визначення номера першого від’ємного елемента вектора Z звертаємось до програми-функції Rez:
Знаходимо значення першого від’ємного елемента:

94
Приклад 3. Задано масив X={3; 0; 7; 1; -4; 0; 2}. Сформувати масив Y, вилучивши з масиву X усі нульові елементи.
Реалізація завдання.
Програма-функція формування вектора з ненульових елементів довільного вектора Z:
Для формування вектора Y звертаємось до програми-функції Rez:
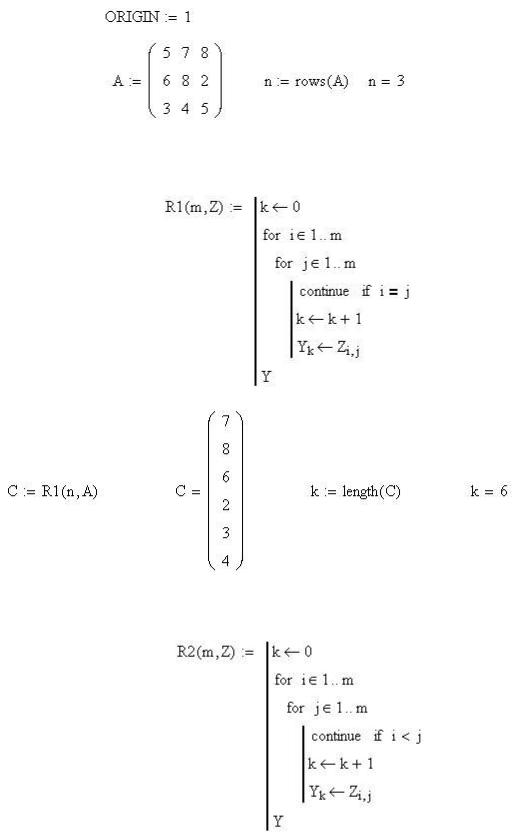
Приклад 4. Сформувати вектор С з елементів, що не лежать на головній діагоналі матриці А, та вектор D з елементів матриці А, які знаходяться на головній діагоналі та нижче її,
|
5 |
7 |
8 |
|
|
де |
|
|
8 |
2 |
|
A 6 |
. |
||||
|
|
3 |
4 |
5 |
|
|
|
|
|||
95
Реалізація завдання.
Програма-функція формування вектора, елементами якого є елементи довільної квадратної матриці Z, що не лежать на головній діагоналі:
Для формування вектора C звертаємось до програми-функції R1:
Програма-функція формування вектора D з елементів довільної квадратної матриці Z, які лежать на головній діагоналі та нижче її:
Для формування вектора D звертаємось до програми-функції R2:

96
Приклад 5.
1) Сформувати матрицю С={Ci,j} i 1,n ; j 1,n ; n 4,
|
Ci, j |
(i j) |
, i j |
|
де |
|
(i j)2 , i j |
||
|
|
|||
2)Сформувати вектор D з елементів матриці С, що задовольняють умові –
20 < Ci,j 4.
3)Сформувати вектор V, елементами якого є суми елементів стовпців заданої матриці С.
4)Сформувати нову матрицю B, вилучивши 2-й рядок з матриці С.
5)Сформувати нову матрицю Q, вилучивши 3-й стовпець з матриці B.
6)Упорядкувати елементи векторів V та D на зростання модулів елементів.
Реалізація завдання.
Формування матриці С:
Програма-функція формування вектора, елементами якого є суми елементів стовпців довільної прямокутної матриці.

97
Для формування вектора V звертаємось до програми-функції Form:
Програма-функція формування вектора з елементів довільної прямокутної матриці, які більше –20, але не перевищують 4.
Для формування вектора D звертаємось до програми-функції Form1:
Програма-функція формування нової матриці вилученням з довільної прямокутної матриці її i1-го рядка.
Для формування матриці B звертаємось до програми-функції VR:

98
Програма-функція формування нової матриці вилученням з довільної прямокутної матриці її j1-го стовпчика.
Для формування матриці Q звертаємось до програми-функції VS:
Програма-функція упорядкування довільного вектора за зростанням модулів його елементів.
Для упорядкування елементів векторів V та D за зростанням модулів їх елементів звертаємось до програми-функції Upor:
99
13. Модульне програмування в MathCAD
Загальна ідея модульного програмування полягає в наступному:
реалізація обчислювальних процесів у вигляді окремих програмних одиниць– модулів;
звернення до цих модулів в інших програмах iз передачею даних, необхідних
для обчислювального процесу.
Модульне програмування дозволяє зменшити обсяг текстів програм, зробити їх більш зрозумілими, прискорити написання і тестування програм, зменшити витрати на супровід (експлуатацію) програм.
Впровадження модульного програмування в пакеті MathCAD можна здійснити двома способами:
1)модульне програмування в межах одного документа MathCAD;
2)модульне програмування в декількох документах MathCAD.
13.1.Модульне програмування
водному документі
Цей спосіб характеризується тим, що:
для реалізації простих обчислень використовуються локальні функції, а більш складних – програми-функції;
опис локальних функцій, програм-функцій та звертання до них знаходяться в
межах одного документа і зберігаються в одному файлі. Такий спосіб має ряд недоліків:
неможливість розробки програм-функцій декількома розробниками;
неможливість "автономного" відлагодження програм-функцій та їх модифікації в процесі експлуатації програмного забезпечення;
неможливість використання розробленої програми-функції в декількох документах без дублювання опису програми-функції.
13.1.1. Функція користувача
Незважаючи на доволі широкий набір вбудованих функцій, завжди виникає необхідність розширити систему новими функціями, в яких зацікавлений користувач.
Формат функції користувача:
Ім’я функції (Список формальних параметрів) := А,
де Ім’я функції – довільний ідентифікатор; Список формальних параметрів
– це використані в виразі А змінні, які розділяються між собою комами; А – довільний арифметичний вираз.

100
Приклад.
f1(x) := 10 (1–cos(x)2) f2(x, y) := ln(x2+y2)
Звернення до функції користувача:
Ім’я функції (Список фактичних параметрів)
Фактичні параметри також розділяються комами. Кількість фактичних параметрів повинна відповідати кількості формальних параметрів.
Дія: Кожному формальному параметру ставиться у відповідність фактичний параметр. Обчислюється арифметичний вираз А і його значення передається в місце звернення.
Приклад.
Зауваження. Функція користувача є найпростішим випадком програми– функції.
13.1.2. Приклади розв’язання задач
Z
де
Приклад 1. Обчислити суму та добуток |
n2 |
|
|
|
|
|
|
||||||||||||||
n2 |
fk (r,p) gk (p,r); |
|
|
|
|
|
|
|
|
|
|
W |
gk (r,p) fk (r,p) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
k n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
k n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
, x y; |
|
|
|
sin |
xy |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
k |
x2 y2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
k |
, |
||||||||||||
fk (x,y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
gk |
(x,y) 1 |
|
|
|||
|
ln(1 k |
|
xy |
|
) |
|
|
1 k2 |
|||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
|
, x y |
|
|
|
||||||||||||
|
|
k |
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1=3; n2=10; p=-1,1; r=0,7.
Реалізація завдання.
Функції користувача:
