
- •Міністерство освіти і науки україни
- •Розподіл лабораторних занять з курсу „фізика” на іі семестр навчання
- •Модуль 1. Магнетизм. Коливання та хвилі Лабораторна робота № 1 визначення горизонтальної складової вектора магнітної індукції магнітного поля землі
- •Теоретичні відомості
- •Порядок виконання роботи
- •Результати вимірювань та вихідні дані для розрахунку похибок
- •Питання для самоперевірки
- •Лабораторна робота № 2 вивчення механічного осцилятора з одним ступенем вільності
- •Теоретичні відомості
- •Порядок виконання роботи
- •Результати вимірювань та вихідні дані для розрахунку похибок
- •Результати вимірювань та вихідні дані для розрахунку похибок
- •Питання для самоперевірки
- •Лабораторна робота № 3 вивчення електричного осцилятора з одним ступенем вільності
- •Теоретичні відомості
- •Опис установки
- •Послідовність виконання роботи
- •Питання для самоперевірки
- •Лабораторна робота № 4 визначення швидкості звуку фазовим методом
- •Теоретичні відомості
- •Порядок виконання роботи
- •Питання для самоперевірки
- •Модуль 2. Оптика Лабораторна робота № 5 визначення радіуса кривини лінзи та довжини світлової хвилі за допомогою кілець ньютона
- •Теоретичні відомості
- •Опис приладу
- •Порядок виконання роботи
- •Визначення довжини хвилі
- •Питання для самоперевірки
- •Лабораторна робота № 6 визначення довжини хвилі жовтої лінії спектра неону за допомогою дифракційної гратки
- •Теоретичні відомості
- •Порядок виконання роботи
- •Питання для самоперевірки
- •Лабораторна робота № 7 визначення концентрації цукру в розчині за допомогою поляриметра
- •Теоретичні відомості
- •Порядок виконання роботи
- •Питання для самоперевірки
- •Лабораторна робота № 8 вимірювання кута розбіжності і ступеня поляризації випромінювання He-Ne лазера
- •Теоретичні відомості
- •1. Вимір розбіжності газового пучка
- •Порядок виконання роботи
- •2. Вимірювання ступеня поляризації лазерного випромінювання
- •Порядок виконання роботи
- •Питання для самоперевірки
- •Модуль 3. Атомна фізика Лабораторна робота № 9 вивчення законів теплового випромінювання речовин та вимірювання температури нагрітих тіл за допомогою оптичного пірометра
- •Теоретичні відомості
- •Опис приладу
- •Питання для самоперевірки
- •Лабораторна робота № 10 вивчення зовнішнього фотоефекту
- •Теоретичні відомості
- •Порядок виконання роботи
- •Питання для самоперевірки
- •Лабораторна робота № 11 вивчення спектрів випромінювання і поглинання різних речовин
- •Теоретичні відомості
- •Опис спектральних приладів
- •Порядок виконання роботи.
- •Питання для самоперевірки
- •Список рекомендованої літератури Основна література
- •Додаткова література
- •Додатки
- •Основні одиниці sі
- •Похідні одиниці sі, що мають спеціальні назви
- •Коефіцієнти Стьюдента
- •Характеристики мір
- •Характеристики приладів
- •Властивості натуральних логарифмів
- •Грецький алфавіт
Лабораторна робота № 3 вивчення електричного осцилятора з одним ступенем вільності
Мета роботи – вивчити закономірності затухаючих коливань електричного осцилятора; отримати експериментально характеристики затухаючих коливань електричного осцилятора; ознайомитися з вимушеними коливаннями електричного осцилятора і порівняти їх з теоретично розрахованими.
Прилади та обладнання: електричний осцилятор; генератор звукових коливань; діод; магазин резисторів; магазин ємностей; котушка індуктивності; перемикач; з'єднувальні дроти.
Теоретичні відомості
Коливальний контур (LС – контур) складається з послідовно з'єднаних індуктивності L і ємності С, і називається також електричним осцилятором (рис. 1).
При вивченні коливань у контурі завжди розглядають зміну тільки однієї з величин – сили струму в контурі, падіння напруги на активному опорі, заряду на обкладках конденсатора або різниці потенціалів між його обкладками .
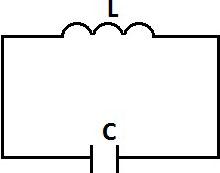
Рис. 1.
Згадаємо,
як виникають коливання в контурі при
активному опорі R
= 0 (рис.
2). Для збудження коливань попередньо
заряджають конденсатор ємністю С
зарядом Q0
(рис. 2, а) і в початковий момент часу t =
0 вся енергія контуру
![]() зосереджена в електричному полі
конденсатора. СтрумI
в контурі відсутній.
зосереджена в електричному полі
конденсатора. СтрумI
в контурі відсутній.
Замкнемо перемикач К (рис. 2, б); через котушку індуктивністю L потече струм I, що буде зростати з часом. Якщо струм І зростає (рис. 3), то збільшується B-вектор магнітної індукції магнітного поля, яке з'являється в котушці. Напрям В зображено на рисунку товстими суцільними стрілками. Відповідно до закону Фарадея у витках котушки індукується електричне поле при зміні магнітного поля. Напрям електричного поля зображено тонкими штриховими стрілками.
Електрорушійна сила (ЕРС) самоіндукції
(1)
Оскільки за правилом Ленца ЕРС εs напрямлена в бік, протилежний зростаючому струму I, то він зростає до максимального значення повільно. При цьому зменшується заряд на конденсаторі. Отже, зменшується електрична енергія поля конденсатора, перетворюючись в енергію магнітного поля котушки індуктивності.
В момент часу (Т - період коливань заряду) Wе=0, Q=0, енергія магнітного поля максимальна.
![]()
а) t=0 б) t=T/4 в) t=T/2 г) t=3T/4






















![]()
![]()
![]()
![]()
![]()

 +
+ - -
+
+ - -






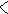










 L - - C C + + C
L - - C C + + C
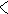




 L L L C
L L L C
I![]()
Рис. 2.
1)![]() 2)
2)![]() 3)
3)![]() 4)
4)![]()
Струм
у контурі починає спадати, тому що
відбувається зарядка конденсатора,
зменшується енергія магнітного поля
![]() ,
зі зменшенням В
з’являється ЕРС:
,
зі зменшенням В
з’являється ЕРС:
![]()
У
цьому випадку εs
напрямлена в бік спадаючого струму.
Згідно з правилом Ленца індукційний
струм напрямлений у той самий бік, що й
струм зарядки конденсатора. До закінчення
часу
![]() на обкладках
на обкладках
конденсатора накопичується максимальний заряд, що спричинює появу максимального електричного поля.
![]()
Струм у колі дорівнює нулеві (див. рис. 2, в).

Рис. 3.
Далі
ті самі процеси почнуть протікати у
протилежному напрямі (рис. 2, г) і система
до моменту часу
![]() повернеться до початкового стану.
повернеться до початкового стану.
За другим правилом Кірхгофа сума падінь напруги у замкнутому контурі дорівнює алгебраїчній сумі ЕРС у контурі. При відсутності активного опору в контурі, тобто при R= 0, всі падіння напруги відбуваються на ємності:
![]() (2)
(2)
Отже,
Враховуючи,
що і
![]() ,
маємо
,
маємо![]() ,
,
або
. (3)
Введемо позначання
. (4)
Тоді
![]() . (5)
. (5)
Де ω0 – циклічна частота власних коливань контура.
Вираз (5) – диференціальне рівняння власних коливань лінійного гармонічного осцилятора, у даному випадку LC — контура.
Якщо розглядати дійсний контур, що крім L і С, має резистор (як резистор може бути опір індуктивності), то разом з падінням напруги на ємності
спостерігатиметься
падіння напруги і на резисторі ![]() і тому другий закон Кірхгофа запишемо
так:
і тому другий закон Кірхгофа запишемо
так:
,
, (6)
![]() ,
,
. (7)
Введемо позначення (4) і
![]() . (8)
. (8)
Дістанемо
![]() , (9)
, (9)
де δ – коефіцієнт затухання.
Вираз (9) – лінійне диференціальне рівняння другого порядку, тобто диференціальне рівняння затухаючого гармонічного осцилятора (LС-контура) з розв'язком
(10)
за
умови, що ![]()
(втрати енергії в системі малі),
де Q - заряд на конденсаторі у визначений момент часу t; Q0 - амплітуда заряду при t = 0; е - основа натуральних логарифмів; ω - циклічна частота затухаючого гармонічного осцилятора,
![]() (11)
(11)
За законом (10) змінюється й напруга на конденсаторі:
![]() (12)
(12)
де
![]() – амплітуда наруги приt=0;
– амплітуда наруги приt=0;![]() - амплітуда напруги при t ≠ 0.
- амплітуда напруги при t ≠ 0.
Отже,
якщо збуджувати контур - заряджати
ємність то за умови
![]() в ньому виникнуть коливання заряду, які
затухатимуть (рис.4).
в ньому виникнуть коливання заряду, які
затухатимуть (рис.4).

Рис. 4.
Закон зміни амплітуди з часом (штрихова лінія)
![]() (13)
(13)
Одна з головних характеристик електричного затухаючого осцилятора - логарифмічний декремент затухання Ө, який визначається як натуральний логарифм відношення двох амплітуд, (Рис.4) віддалених одна від одної на період Тз:
 .
(14)
.
(14)
Друга характеристика – період затухання
![]() .
(15)
.
(15)
Час, протягом якого амплітуда зменшується в е разів, називається часом релаксації τ:
![]() ,
(16)
,
(16)
де
![]() або
або
![]() .
.
Важлива особливість електричного осцилятора - добротність Qдоб яка дорівнює добутку числа коливань Nе, що відбуваються за час, протягом якого амплітуда коливань зменшується в е разів, і числа π:
![]() .
(17)
.
(17)
Характеристики (14), (16) і (17) взаємопов'язані:
![]()
і залежать від параметрів електричного осцилятора:
 (18)
(18)
При ![]() (19)
(19)
 (20)
(20)
При
![]()
![]() (21)
(21)
![]() (22)
(22)
При
![]()
![]() (23)
(23)
При
![]() втрати енергії в системі великі через
великий опірR1
контура. У цьому разі в (10) перший член
не має суттєвого значення і розв'язок
описує аперіодичний режим руху заряду
- коливання не відбуваються (рис. 5).
втрати енергії в системі великі через
великий опірR1
контура. У цьому разі в (10) перший член
не має суттєвого значення і розв'язок
описує аперіодичний режим руху заряду
- коливання не відбуваються (рис. 5).

Рис. 5.
Опір,
при перевищенні якого в системі немає
коливань, називається критичним. Його
знаходять за умови
![]() (див. (4) і (8):
(див. (4) і (8):
![]()
![]() (24)
(24)
Потреби практики диктують необхідність мати тривалі незатухаючі коливання у контурі. Коливальний процес стане не затухаючим, якщо на контор діятиме зовнішня сила, що періодично змінюється. Такі коливання називають вимушеними. Вимушені коливання в електричному контурі можна дістати, якщо в нього ввімкнути генератор сигналів, наприклад, звуковий генератор ЗГ.
Диференціальне рівняння вимушених коливань у контурі дістають з рівняння затухаючих коливань (7), якщо в нього додати періодичну ЕРС
![]() (
(![]() – циклічна частота періодичної ЕРС):
– циклічна частота періодичної ЕРС):
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
(25)
,
(25)
де
![]() –
амплітудне значення напруги в коливальному
контурі.
–
амплітудне значення напруги в коливальному
контурі.
Розв'язок (25):
![]() ,
(26)
,
(26)
де Q0 - амплітуда заряду на конденсаторі.
Напруга на обкладках конденсатора змінюється за законом
![]() ,
,
де U0 - амплітуда напруги на конденсаторі,
 ,
(27)
,
(27)
a зсув фаз між коливаннями змушуючої сили (коливаннями напруги на виході звукового генератора) і коливаннями напруги на конденсаторі
 .
(28)
.
(28)
У
разі вимушених коливань - величина
відставання за фазою вимушеного коливання
заряду
![]() (26) від спричиняючої його змушуючої
періодичної ЕРС.
(26) від спричиняючої його змушуючої
періодичної ЕРС.
Залежність
амплітуди вимушених коливань від
змушуючої сили можна дослідити на
максимум і переконатися, що
![]() максимальна при результуючій частоті
періодичної ЕРС
максимальна при результуючій частоті
періодичної ЕРС
![]() .
(29)
.
(29)
Ця
частота називається резонансною, а саме
явища зростання амплітуди при наближенні
до резонансної частоти або кратної їй
– резонансом. Фаза вимушених коливань
при
![]() збігається з фазою змушуючого впливу;
в околі резонансу при
збігається з фазою змушуючого впливу;
в околі резонансу при![]() різниця фаз наближається до
різниця фаз наближається до![]() ,
а при
,
а при
![]() – до
– до![]() тобто фаза коливань майже протилежна
фазі змушуючої сили.
тобто фаза коливань майже протилежна
фазі змушуючої сили.
Амплітудні криві для трьох різних значень втрат в системі:
![]() зображено
на рис. 6.
зображено
на рис. 6.
У
техніці добротність осцилюючої системи
визначає відносну гостроту резонансного
піку, оскільки
![]() обернено пропорційна коефіцієнту
затухання (16).
обернено пропорційна коефіцієнту
затухання (16).
