4.12. Раскраска ребер графа и теоремы о хроматическом классе

Пусть дан связный неориентированный граф G. Раскрасим его ребро в какой‑либо цвет. Раскраска назы­ва­ется правильной, если никакие два ребра, инцидентных дан­ной вершине, не окрашены в один и тот же цвет.

Наименьшее число q цветов, достаточных для пра­виль­ной раскраски графа называется хроматическим клас­сом. Пусть ρ_max — наибольшая из степеней вершин графа. Тогда, очевидно, ρ_max < q.

В задачах, связанных с применением информационных технологий, вершины графа G можно интерпретировать как некоторые узлы — информационные центры, способные принимать и передавать информацию по каналам — ребрам графа G. Каждый такой канал должен иметь уникальный ад­рес на множестве всех адресов данного узла. В качестве та­кого адреса можно принять цвет, отвечающий правильной рас­краске графа G. Возникает вопрос. Какова должна быть минимальная мощность множества всех адресов инфор­ма­ционных каналов для того, чтобы обеспечить воз­можность однозначной адресации между всеми инфор­мационными це­нтрами? Ясно, что множество всех таких адресов составляет хроматический класс графа G.

Для хроматических графов Шенноном доказана сле­дующая теорема, которую мы приводим без доказательств.

Теорема 4.15 (Шеннон) Хроматический класс графа не превосходит 3 ρ_max / 2, где символами а обозначено наименьшее целое, не превосходящее вещественное a.

Приведем пример, когда эта оценка не улучшаема. Действительно, если множество вершин графа состоит из трех точек a,b и c, а степени вершин равны соответственно (a) = (b) = k и (c) = 2k / 2, то для правильной его раскраски потребуется точно 3k / 2 цветов. Например, если (a) = (b) = 3, а (c) = 2k / 2 = 2, то для правильной раскраски этого графа потребуется четыре цвета.

Оценка, полученная Шенноном, может быть улучшена для некоторых частного вида графов. Некоторые такие графы рассмотрены В.Г.Визингом.

Теорема 4.16 (Визинг) Пусть R — наибольшее число ребер между смежными вершинами. Тогда

q  ρ_max + R.

Представляет интерес рассмотреть случай, когда R = 1.

Тогда равенство q = ρ_max + 1 достигается при четном ρ_max  2 для полного графа U _ρmax+1. Пусть ρ_max = 2m > 0. В этом случае граф U _ρmax+1 имеет 2m + 1 вершину и среди любых m + 1 его ребер хотя бы два имеют общую вершину. Поэтому окрасить одним цветом можно не более, чем m его ребер. Так как всего он имеет (2m + 1)m ребер, то должно выполняться неравенство

qm  (2m + 1)m или q  (2m + 1) = ρ_max + 1.

По теореме же Визинга q  ρ_max + 1. Следовательно, имеет место точное равенство q = ρ_max + 1.

Задачи

Построить графы для решения задач 4.1 — 4.2.

4.1 Перевозчику (П) нужно переправить через реку волка (B), козу (К) и мешок с капустой (М). Лодка так мала, что кроме перевозчика может взять только один из этих объектов. Кроме того, капусту нельзя оставлять вместе с ко­зой, а козу — с волком. Как можно осуществить переправу?

4.2 Два человека имеют полный кувшин воды в 8 литров, а также два пустых кувшина в 5 и в 3 литра. Как они могут разделить воду поровну?

4.3 Пусть имеется множество V, состоящее из 3 доку­ментов. Построить граф для отношения a  A, харак­те­ри­зу­ющий принадлежность документа a множеству A, где A про­бегает все подмножества множества V.

4.4 Пусть имеется множество T, состоящее из трех ко­м­пью­терных сетей: S1, S2, S3. Известно, что компьютер K1 входит только в сеть S1, компьютер K2 — только в сеть S2, а компьютер K3 входит в две сети: S1 и S2. Построить граф, характеризующий принадлежность компьютера компьютер­ным сетям.

4.5 Показать, что два графа на данном рисунке изоморфны.

4.6 Потоки документов циркулируют между городами A₁, A₂, A₃ и городами B₁, B₂, B₃. Можно ли проложить не­пересекающиеся маршруты, соединяющие каждый город A_i с каждыми городом B_j?

4.7 Найти степени вершин для графов тетраэдра и ку­ба.

4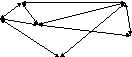.8Найти сумму степеней всех вершин для следующего графа:

4.9 Построить матрицы смежности и инцидентности для тетраэдра.

4.10 Являются ли эйлеровыми графами: прямоугольник с главной диагональю, куб?

4.11 Какова мощность минимального покрытия куба цепями?

4.12 На графе, который определен прямоугольником с непересекающимися диагоналями построить покрытие графа цепями.

4.13 Решить задачу о званом обеде, когда число участников обеда равно 5: хозяин — мужчина. Остальные две пары (мужчина, женщина) — гости. Хозяин знаком со всеми приглашенными мужчинами. Обе женщины знакомы друг с другом.

4.14 Привести любое решение задачи шахматного коня.

4.15 Применив алгоритм с возвратами построить все га­мильтоновы циклы для графа, образованного квадратом с пересекающимися диагоналями.

4.16 Подсчитать, сколько каталогов можно построить в WINDOWS, если всего имеем 5 папок.

4.17 Для некоторой информационной сети, состоящей из 4 абонентских пунктов известны стоимости сооружения любого из ее участков. Эти стоимости приведены ниже.

Таблица 4.1

Пункты	Стоимости (тыс. гривен)
	1	2	3	4
1	—	2	3	5
2	2	—	3	4
3	3	3	—	6
4	5	4	6	—

Используя алгоритм Борувки, спроектировать инфор­мацион­ную сеть минимальной стоимости.

4.18 Граф представлен ромбом с диагональю. Является ли он бихроматическим?

4.19 Пусть все n городов имеют друг с другом по одному информационному каналу связи. Применив теорему Визинга определить минимальное число адресов каналов.