4.4. Степени вершин графа

Пусть G — неориентированный граф.

Локальной степенью (степенью) вершины v в графе G без петель называется число ребер (v), инцидентных этой вершине.

Теорема 4.3 Сумма степеней всех вершин графа без петель равна удвоенному числу m его ребер:

_iⁿ _{= 1} (v_i) = 2m (4.1)

Доказательство. Подсчет всех степеней вершин графа можно вести по вершинам. Количество ребер, инцидентных вершине v, равно (v). Но при этом каждое ребро считается дважды: в начальной и конечной вершинах. Следовательно, имеет место (4.1).

Теорема 4.4 Число вершин, имеющих нечетную степень, четно.

Доказательство. Обозначим ₁ и ₂ — количество всех вершин графа, имеющих нечетную и соответствен­­но — четную степень. По теореме 4.3 имеем ₁ + ₂ = 2m. Следовательно, ₁ = 2m - ₂. Правая часть этого соотношения четна. Поэтому четна и левая. Теорема доказана.

Граф G называется однородным степени r, если локальные степени всех его вершин равны r. Примерами та­ких графов являются правильные многогранники: куб, ок­та­эдр и т.д..

Из формулы (4.1) следует, что в однородном графе степени r число ребер равно:

m = nr / 2. (4.2)

Рассмотрим теперь случай ориентированного графа G.

Обозначим через (v) и *(v) числа ребер выходящих из вершины v и соответственно входящих в вершину v. Эти числа называются локальными степенями вершины v.

Для числа ребер в G, аналогично (4.1) имеем:

m = _iⁿ _{= 1} (v_i) = _iⁿ _{= 1} *(v_i) (4.3)

Ориентированный граф называется однородным степе­ни n, если все его локальные степени имеют одно и тоже значение

(v) = *(v) = n (4.4)

для любой вершины из G.

Для однородного ориентированного графа имеет место соотношение, аналогичное (4.2):

m = nr (4.5)

4.5. Представление графов матрицами

Матричные представления графов используются при решении прикладных задач, особенно в тех случаях, когда при моделирование предметной области применяются ал­ге­браические доказательства.

Пусть имеем граф G(V, U). Его матрицей смежности называется квадратная матрица (a_ij) порядка n², где n — чи­сло вершин, а a_ij — число ребер, инцидентных вершинам v_i и v_j. Если граф не имеет кратных ребер, то a_ij = 1, когда v_i и v_j смежные и a_ij = 0, когда v_i и v_j не смежные. Если граф не имеет петель, то все его диагональные элементы равны нулю.

Рассмотрим примеры. На рисунке 4.8 изображены три неориентированных графа.

а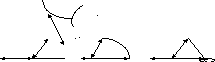)v₁ б) v₁ в) v₁

v₃ v₂ v₄ v₃ v₂ v₄ v₃ v₂ v₄

Рисунок 4.8

В первом случае (рисунок 4.8 а) имеем граф без петель и без кратных ребер. Во втором случае (рисунок 4.8 б) имеем кратные ребра. В третьем случае (рисунок 4.8 в) в вер­шинах v₁ и v₄ имеются петли. Соответствующие этим трем случаям матрицы смежности представлены ниже:

а) 0 1 0 1 б) 0 2 0 3 в) 0 1 0 1

1 0 1 1 2 0 1 1 1 0 1 1

0 1 0 0 0 1 0 0 0 1 0 0

1 1 0 0 3 1 0 0 1 1 0 2

Для неориентированного графа матрица смежности яв­ляется симметрической: для любых i, j ≤ n имеем a_i,j = a_j,i. Для ориентированного графа мат­ри­ца смежности симмет­ричес­кой, вообще говоря, не явля­ет­ся.

Матрицей инциденций неориентированного графа назы­вается матрица (a_ij) размера n m, где n — число вер­шин, а m — число ребер, построенная по правилу:

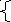1, если i‑тая вершина инцидентна j‑тому ребру,

а_ij =

0 — в противном случае.

Так, соответствующая рисунку 4.8 б матрица инциденций представлена ниже:

Примечание.

Для графа на рисунке 4.8 б приняты следующие обозначения ребер:

a₁ = (v₁,v₂)₁, a₂ = (v₁,v₂)₂, a₃ = (v₁,v₄)₁, a₄ = (v₁,v₄)₂, a₅ = (v₁,v₄)₃, a₆ = (v₂,v₄), a₇ = (v₂,v₃).

1 1 1 1 1 0 0

1 1 0 0 0 1 1

0 0 0 0 0 0 1

0 0 1 1 1 1 0 .

Матрица инциденций неориентированного графа обладает следующими очевидными свойствами:

• в графе без петель каждый столбец этой матрицы имеет в точности две единицы, соответствующие паре вершин ребра,

• если в графе имеются петли, то в столбцах, соответствующих петлям, имеется по одной единице, а в остальных — по две.

Матрицей инциденций ориентированного графа назы­­вается матрица (а_ij) размера n m , где n — число вершин, а m — число ребер, построенная по правилу:

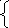1, если i‑тая вершина начальная для j‑того ребра,

а_ij = -1, если i‑тая вершина конечная для j‑того ребра,

0, в случае, когда вершина и ребро не инцидентны.

Рассмотрим, например, граф, изображенный на ри­­сунке 4.9.

v₅

v₂ 

v₄ 

v₃ v₆

v₁ 

Рисунок 4.9

Построенная, в соответствии с описанным правилом, матрица инциденций этого графа имеет вид:

Примечание.

Для графа на рисунке 4.9 приняты следующие обозначения дуг:

a₁ = (v₁,v₂), a₂ = (v₁,v₃), a₃ = (v₃,v₂),

a₄ = (v₃,v₄), a₅ = (v₅,v₄), a₆ = (v₅,v₆),

a₇ = (v₆,v₅).

1 1 0 0 0 0 0

-1 0 -1 0 0 0 0

0 -1 1 1 0 0 0

0 0 0 -1-1 0 0

0 0 0 0 1 1 1

0 0 0 0 0 0 -1 .

Ориентированный граф, как правило, петель не содержит. Его матрица инциденций имеет в каждом столбце +1 и -1, которые отвечают началу и концу каждого ребра.