3.3. Перестановки, подстановки и их свойства

Рассмотрим теперь частный случай инъективных размещений, когда r = n, по‑прежнему полагая, что n‑X = ={1, 2, …, n}.

В этом случае мы можем считать, что имеет место биекция f: n‑X→ n‑X. Любая такая биективная функция име­нуется — подстановка. Результат ее применения к мно­жеству n‑X называется перестановкой.

Подстановки обозначаются символами « f», «g», «h» или другими латинскими буквами.

Подстановка задается в виде биективной таблицы, где верхняя строка представляет исходный элемент, а ниж­няя — полученный из исходного, путем изменения порядка компонент элемента. Например, подстановка

1 2 3

f =

3 2 1

переводит элементы множества {1, 2, 3} так: 1 в 3, 2 в 2, а 3 в 1.

В другом примере, таблицы

1 2 3 1 2 3 1 2 3

2 2 2 2 2 1 4 5 6

подстановками не являются: в первом и во втором примерах разные элементы переходят в один и тот же элемент, а в треть­ем появились значения, не принадлежащие X = {1, 2, 3}.

Задача получения множества всех подстановок на n‑X эквивалентна задаче получения всевозможных перестановок местами элементов соответствующего n‑X упорядоченного множества. Так из множества всех функций, полученных при решении задачи о размещениях при n = r = 3 имеем перестановки:

1, 2, 3 , 1, 3, 2, 2, 1, 3, 2, 3, 1,  3, 1, 2,  3, 2, 1.

Далее нам понадобится понятие факториала целого положительного числа n. Так именуется обозначение n!. (Сим­волы «n! « читаются — «n‑факториал»).

Значение n! определяются следующим образом:

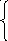
1, если n = 0,

n! =

12n, если n > 0.

Теорема 3.3 Число всех перестановок множества n‑X равно

A_nⁿ = n! (3.9)

Доказательство. Все перестановки множества n‑X определяются множеством всех подстановок из n‑X на n‑X. Поэтому полагая в формуле (3.7) n = r, получим

A_nⁿ = n(n - 1∙∙∙(n - (n - 1)) = n(n - 1)∙∙∙1 = n!,

что и требовалось.

Поскольку любая подстановка осуществляет биекцию из n‑X на n‑X, то это наводит на мысль, что можно запи­сывать подстановки в виде одной строки, рассматривая со­седние элементы, как подстановки из x_i → x_i+1 →… . В связи с тем, что множество n‑X конечно, этот процесс должен за­кончиться на том же элементе, на котором начался, а затем повториться. Поэтому однострочные подстановки называют цик­лами. Одной подстановке может соответствовать неко­торое множество циклов. Поясним это на примере.

1 2 3 4 5 6 7 8

Пусть f =

4 5 6 7 8 3 2 1 .

Тогда 1→ 4, 4→ 7, 7→ 2 … и можно разложить подстановку в произведение двух циклов, области которых отмечены квадратными скобками.

f = [1 4 7 2 5 8 ][3 6]

Пусть дана подстановка f = [x₁, x₂, …, x_n]. Пару (x_i, x_j) (i < j) будем называть инверсией подстановки f, если x_i > x_j. Подстановка называется четной, если число инверсий в ней четно и нечетной в противном случае.

Так подстановка [1 4 7 2 5 8 ] имеет следующие инверсии: (4 2), (7 2), (7 5), (8 1) и, следовательно, является четной.

Подстановка называется транспозицией, если она пре­дставляет цикл длины два.

Понятия инверсии и транспозиции используются, в частности, для упорядочения множеств.

Пусть элементы n‑X расположены в случайном порядке. Составим предикат: p(x_i, x_j) = 1 тогда и только тогда, когда имеет место инверсия x_i, x_j. Пусть также функция transp(x_i, x_j) осуществляет транспозицию элементов x_i, x_j, то есть переставляет их местами. Тогда алгоритм

«выталкивает» наибольший элемент в конец списка элементов множестваn‑X. Решая эту же задачу повторно, для элементов множеств (n - j)‑X, (j = 1, n - 1) можно упорядочить все элементы n‑X по возрастанию. Алгоритм упорядочения запишется так: В программировании он именуется как «пузырьковая сортировка».

Множество всех подстановок n‑X множества обознача­ют S_n.

В алгебре этими же символами обозначают так называемую симметрическую группу. Рассмотрим, с чем связано применение понятия группы к перестановкам.

Произведением подстановок f и g называют подстановку, полученную последовательным применением вначале подстановки f, а затем — g и пишут gf. Например, если

1 2 3 1 2 3

f = , g = ,

3 2 1 2 3 1

1 2 3

то gf = .

1 3 2

Непосредственно проверяется, что операция произведения подстановок свойствами коммутативности, вообще говоря, не обладает. Для того чтобы убедиться в этом, достаточно рассмотреть в предыдущем примере произведение fg. Применяя последовательно вначале g, а потом f, получим

1 2 3

fg =

2 1 3 .

Докажем, что операция произведения подстановок ассоциативна, то есть (hg)f = h(gf).

Пусть a — произвольная компонента элемента перестановки, которая применением f переходит в b. Запишем это так

a  ^f b .

Пусть также имеем b  ^g c и с  ^h d .

Тогда последовательно применяя, вначале (hg)f, а затем h(gf), получим

a  ^f b, b  ^hg d  a ^(hg)f d;

a  ^gf c, c  ^h d  a ^h(gf) d,

что и требо­ва­лось.

Говорят, что множество G образует группу, если каждой паре элементов f, gG поставлен в соответствие элемент h = gf  G так, что (hg)f = h(gf) и при этом для любого fG существует обратный элемент f ^-1G, такой что f ^-1f = е.

Нетрудно заметить, что в силу свойства биекции, данного по определению, для любой f  S_n однозначно определена обратная подстановка, обозначаемая f^-1, которая при­над­лежит G. Для того, чтобы ее получить, достаточно поменять строки в записи f. Если теперь обозначить е — тождественную подстановку, то есть подстановку, переводящую каж­дый элемент в себя, то становится видно, что для всех f G имеем f ^-1f = е.

Рассмотрим пример. Пусть

1 2 3 3 1 2 1 2 3

f = , тогда f ^-1 = и ff ^-1 =

3 1 2 1 2 3 1 2 3 .

Из перечисленных свойств множества S_n следует, что оно образует группу.

В настоящее время понятие группы широко применяется в различных математических построениях. Ни­же мы используем групповые свойства перестановок для исследования структуры соединений.