Розділ іii. Вступ до аналізу.

§1. Означення функції. Основні поняття та властивості функцій. Графік функції.

Дійсні числа. Модуль числа та його властивості.

Дійсним числом називається будь-який десятковий дріб, скінчений чи нескінчений. Якщо – деяка множина дійсних чисел, то записозначає, що числоналежить. Відомо, що кожному дійсному числу на числовій осі відповідає єдина точка.

Множина дійсних чисел ( або точок на числовій осі), що задовольняють нерівності(), де– фіксовані числа, називається інтервалом ( відрізком ) і позначається().

Множина дійсних чисел , що задовольняють нерівностіабо, називається півінтервалом.

Надалі, у випадках коли належність чи неналежність множині граничних точок немає суттєвого значення, інтервал, відрізок, півінтервал будемо називати проміжком і позначати.

Інтервал ,називається– околом точки.

Для позначення відстані довільної точки числової осі до початку координат використовують– модуль числа.

Означення. Модулем числа називається

Наприклад: .

Властивості модуля:

1. 2.

3. 4.

5.6.

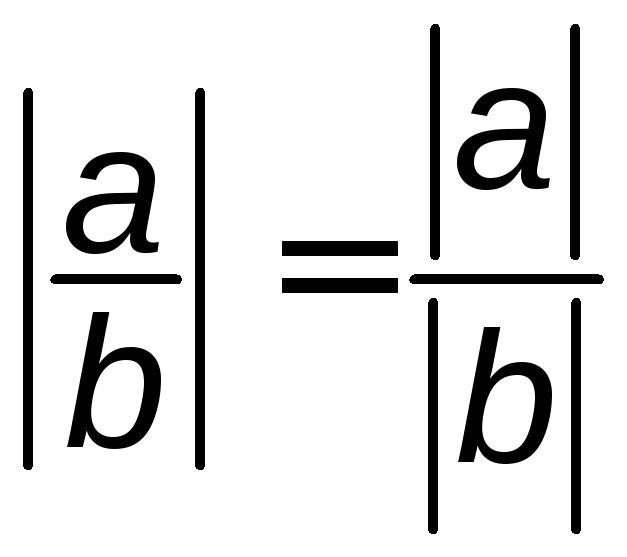
7. Нерівність означає, що.

Означення та способи задання функції. Графік функції.

Нехай задано множину чисел . Говорять, що на множинізадано функцію, якщо кожномувідповідає одне певне числоі записують. При цьомуназивають незалежною зміною або аргументом, а– залежною зміною або функцією.

Множина називається областю визначення функції і позначаєтьсяабо,– значення функції в точці, а сукупністьвсіх таких значень – областю значень функції і позначаєтьсяабо.

З означення функції випливає, що функція вважається заданою, якщо вказано закон відповідності і область визначення. Якщо область визначення функції складається з усіх, для яких виразмає значення, то таку область визначення будемо називати максимальною областю визначення або областю існування. В подальших прикладах знаходження області визначення функції пов’язане тільки із знаходженням області існування.

Приклад 1.1. Знайти область визначення функції .

Розв’язування. Очевидно, що вираз має сенс тоді і тільки тоді, коли, або. Так як, то. Згідно властивості 7 модуля. Отже, область визначення функції є відрізок.

Нехай функція визначена на множині, а функція– на множині. Якщо перерізне є порожня множина, то на цьому перерізі можна визначити суму, різницю, добутокі часткудвох функцій ( останню лише при умові).

Графіком функції з областю визначенняназивається множина всіх точокплощини, координати яких пов’язані даною функціональною залежністю. Найчастіше функція задається на проміжку, а її графіком буде деяка крива. Проте не слід думати, що графіком щоразу буде деяка крива. Це може бути надто складне геометричне місце точок.

Функція може бути задана одним з основних способів: аналітичним, табличним або графічним. Вважають, що функція задана аналітично, якщо вона задана за допомогою однієї або кількох формул на різних проміжках.

Нехай на площині дано прямокутну систему координат . Тоді будь-яка крива в цій площині задає деяку функціювід, якщо всяка пряма, паралельна осі, перетинає цю криву не більше ніж в одній точці. Це графічний спосіб задання функції.

Функцію можна задати і за допомогою таблиці, в одному рядку якої записані значення однієї величини, а в іншому – відповідні значення другої величини, що залежить від першої.

Зауваження. Якщо функція задана аналітично, то неважко перейти до табличного або графічного способу задання функції. Перехід від табличного або графічного способів задання функцій до аналітичного вимагає певних знань та навичок.

Завдання для самостійного розв’язування.

1.1 Знайти область визначення функцій:

а) ; б);

в) ; г);

Відповіді:

1.1 а) б)

в) г)

Складена функція.

Нехай функція визначена на множині, а функціяна множині, причому для всіхвідповідне значенняналежить множині. Тоді на множинівизначена функція, що називається складеною функцією від, або суперпозицією функційі.

Наприклад, функція визначена на множині, а функціявизначена на множиніі має область зміни. Так як множина, то суперпозиція цих функційвизначена на множині.

Проте може статись так, що іне мають спільних точок, тоді відповідні функціїіне утворюють суперпозицію. Наприклад, функціїітакі, щоіне мають ні однієї спільної точки. Таким чином, виразне задає функції від.

Класифікація та деякі властивості функцій.

В багатьох випадках знання особливостей функцій допомагає побудувати їх графіки. Розглянемо деякі типи функцій.

Означення. Функція , визначена на множині, називаєтьсяобмеженою на цій множині, якщо існує таке число, що для всіхвиконується нерівність.

Протилежне поняття формулюється так:

Означення. Функція називається необмеженою на множині , якщо для будь-якого, існуєтаке, що виконується нерівність.

Графік обмеженої функції розміщується між двома прямими, паралельними осі :та.

Означення. Функція , визначена на проміжку, називається зростаючою ( неспадною, спадною, незростаючою) на цьому проміжку, якщо для всіхіз цього проміжку , що задовольняють нерівностівиконується нерівність(,,).

Зростаючі, спадні, неспадні та незростаючі функції називаються монотонними, а зростаючі і спадні, крім того називають строго монотонними. Графіки цих функцій зображені на рис.1

Рис.1.

Означення. Функція , визначена на множині, розміщеній симетрично відносно початку координат, називаєтьсяпарною ( непарною ), якщо для виконується рівність().

Графік парної функції симетричний відносно осі (Рис.2), а графік непарної функції – симетричний відносно початку координат (Рис.3). Ця особливість графіків парної та непарної функцій дає змогу скоротити роботу з побудовою графіків таких функцій: досить побудувати графік функції тільки в правій півплощині.

Рис.2 Рис.3

Обернена функція.

Нехай функція визначена на відрізку, а множиною її значень є відрізок, тобто,.

Якщо кожному значенню відповідає єдине значення, для якого, то на відрізкуможна визначити функцію, яка називається оберненою по відношенню до функції.

Зауваження. Означення оберненої функції може бути узагальнено і для випадків коли іє будь-які проміжки, а не тільки відрізки.

Приклад. Функція визначена на. Оберненою для неї є функція, що також визначена на.

Проте не всяка функція має обернену. Так функція, оберненої не має, оскільки двом різним точкамівона ставить у відповідність одну точку. Сформулюємо теорему існування оберненої функції:

Теорема. Якщо функція строго монотонна на відрізку, то обернена функціяіснує і строго монотонна на відрізку.

Функція , має обернену, оскільки кожним двом різним точкам, вона ставить у відповідність дві різні точки.

Легко помітити, що не є монотонною для, а функціяє зростаючою на проміжку.

Елементарні функції.

Означення. Основні елементарні функції: степенева , показникова, обернена до степеневої, логарифмічна, тригонометричніобернені тригонометричніа також функції, знайдені за допомогою формул, що містять скінчене число арифметичних дій (додавання, віднімання, множення, ділення) і суперпозицій основних елементарних функцій, називаються елементарними функціями.

З основними елементарними функціями ми познайомились в шкільному курсі математики, а тому їх властивості пропонуємо розглянути самостійно.