Определитель матрицы.

Пусть - квадратная матрица- го порядка.

Определение 1.10. Определителем матрицы называется число, которое вычисляется по заданному правилу и обозначается

,

синонимом слова «определитель» является слово «детерминант».

Пример 1.5. а) Пусть , тогда. Например, если, то;

б) Пусть , тогда. Например, если

, то .

Для вычисления определителей матриц более высокого порядка необходимы

Определение 1.11. Минором элементаназывается определитель матрицы, полученной исключением из матрицы- ой строки и- го столбца.

Определение 1.12. Алгебраическим дополнением элементаназывается число, задаваемое формулой.

Теорема Лапласа. Определитель матрицы равен сумме произведений элементов произвольной строки (или столбца) на их алгебраические дополнения

, где .

Теорема Лапласа позволяет перейти от вычисления определителя n – го порядка к вычислению n определителей (n-1) – го порядка, или, после (n-2) применений, к вычислению 0,5 n! определителей второго порядка.

Пример 1.6. Вычислить

.

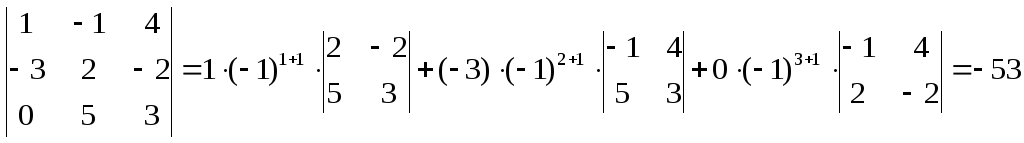Замечание. Очевидно, что существует шесть различных способов вычисления данного определителя с помощью теоремы Лапласа. Разложение по первому столбцу было выбрано, потому что один из элементов в данном столбце равняется нулю. Вычислите этот определитель другим способом и сравните результаты.

замечание о применении компьютерной техники

Свойства определителей

Рассмотрим некоторые свойства определителей, проводя доказательства для определителей матриц второго порядка. Пусть , тогда.

Свойство 1. При транспонировании матрицы её определитель не меняется: .

Доказательство. .

Следствие. При вычислении определителей строки и столбцы матрицы имеют одинаковые свойства (равноправны), поэтому говоря в дальнейшем «строка», будем подразумевать строку или столбец.

Свойство 2. Если в матрице поменять местами две строки, то её определитель поменяет знак.

Доказательство. .

Свойство 3. Если в матрице две одинаковые строки, то её определитель равен нулю.

Доказательство. .

Свойство 4. Если произвольную строку матрицы увеличить в раз, то определитель данной матрицы тоже увеличится враз.

Доказательство. .

Следствие. Если матрица содержит нулевую строку или две пропорциональные строки, то её определитель равен нулю.

Свойство 5. Если к элементам одной строки матрицы прибавить элементы другой строки, умноженные на одно и то же число, то определитель матрицы не изменится.

Доказательство. .

Замечание. Свойство 5 позволяет обнулять некоторые элементы матрицы, не меняя её определителя. С помощью этого можно упростить вычисление определителя

,

вначале обнуляя элемент , а затем разложив по первому столбцу (по теореме Лапласа).

Свойство 6. Сумма произведений элементов одной строки матрицы на алгебраические дополнения к элементам другой строки равна нулю

Доказательство. .

Следствие. Из свойства 6 и теоремы Лапласа вытекает, что .

Свойство 7. Пусть и- квадратные матрицы порядка, тогда.

!Доказательство этого свойства самостоятельно только для желающих участвовать в конференции!

Следствие. Поскольку , то из свойства 7 вытекает, что.

Свойство 8. Определитель треугольной (в том числе диагональной) матрицы равен произведению её диагональных элементов.