
Тема I. Линейная алгебра Матрицы и операции над ними.
Определение 1.1.
Матрицей размерности
![]() называется прямоугольная таблица чисел,
состоящая из
называется прямоугольная таблица чисел,
состоящая из![]() строк и
строк и![]() столбцов. Числа, составляющие таблицу,
называются элементами матрицы.
столбцов. Числа, составляющие таблицу,
называются элементами матрицы.
Для обозначения
матриц используют заглавные буквы
латинского алфавита: А, В, С, …; для
обозначения элементов – строчные буквы
с двойной индексацией:
![]() ,
где i – номер строки, в которой находится
элемент, j – номер столбца
,
где i – номер строки, в которой находится
элемент, j – номер столбца
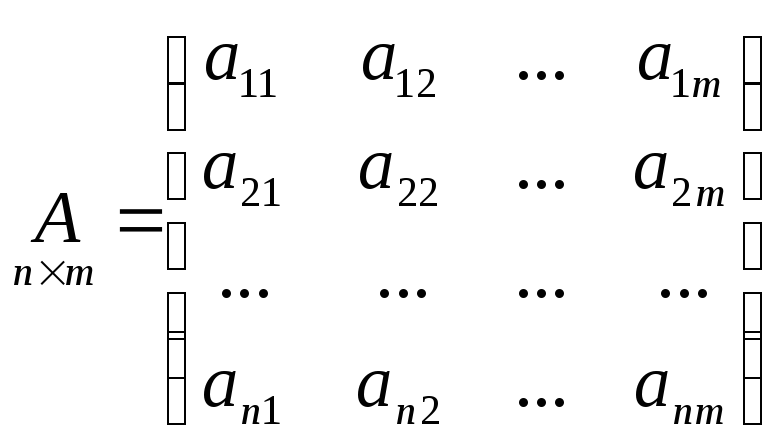
или, в сокращённой
записи,
![]() .
.
Пример 1.1.
Матрица
![]() ,
элементы
,
элементы![]() и
и![]() .
.
Замечание. Наряду с круглыми скобками для обозначения матриц используются также и другие символы: [ ], || ||.
Виды матриц.
Определение 1.2.
Матрица размерности
![]() называется матрицей – строкой (вектором
– строкой), а
называется матрицей – строкой (вектором
– строкой), а![]() - матрицей – столбцом (вектором –
столбцом).
- матрицей – столбцом (вектором –
столбцом).
Определение 1.3. Матрица называется нулевой, если все её элементы равны нулю.
Определение 1.4. Матрица называется квадратной, если число строк совпадает с числом столбцов (n=m). Число n называется порядком матрицы.
Определение 1.5. Элементы квадратной матрицы, у которых i=j: a11, a22,…,ann, называются диагональными и образуют главную диагональ матрицы.
Определение 1.6. Квадратная матрица, у которой все элементы, расположенные под (над) главной диагональю, равны нулю, называется верхней (нижней) треугольной.
Определение 1.7. Квадратная матрица, у которой все недиагональные элементы равны нулю, называется диагональной.
Определение 1.8. Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной и обозначается Е.
проиллюстрировать определения 1.2 – 1.8 на примерах
Действия над матрицами.
1) Сравнение матриц.
Матрицы одинаковой
размерности равны между собой, если
равны их соответствующие элементы:
![]() =
=![]()
![]() .
.
2) Умножение матрицы на число.
Произведением
матрицы
![]() на число
на число![]() будет матрица
будет матрица![]() ,
элементы которой вычисляются по правилу
,
элементы которой вычисляются по правилу![]() .
.
Следствие. Общий множитель всех элементов можно выносить за знак матрицы.
3) Сложение (вычитание) матриц.
Суммой (разностью)
двух матриц одинаковой размерности
![]() и будет матрица
и будет матрица![]() ,
элементы которой вычисляются по правилу
,
элементы которой вычисляются по правилу![]() .
.
Пример 1.2.
Даны матрицы
![]() ,
,![]() .
Найти матрицу
.
Найти матрицу![]() .
.
Решение. 1)
![]()
![]() ;2)
;2)
![]() .
.
Определение 1.9. Две матрицы называются согласованными, если количество столбцов в первой матрице равно количеству строк во второй.
4) Умножение матриц.
Произведением
двух согласованных матриц
![]() и
и![]() будет матрица
будет матрица![]() ,
элементы которой вычисляются по правилу
,
элементы которой вычисляются по правилу![]() ,
то есть являются скалярным произведением
,
то есть являются скалярным произведением![]() –
ой строки первой матрицы на
–
ой строки первой матрицы на![]() –
ый столбец второй.
–
ый столбец второй.
Пример 1.3.
Даны матрицы
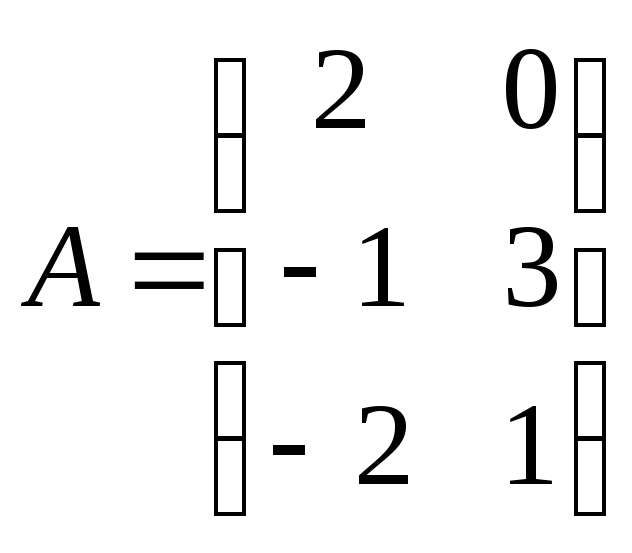 ,
,![]() .
Найти матрицу
.
Найти матрицу![]() .
.
Решение.
Матрицы являются согласованными (2=2),
поэтому их произведение существует.
Это будет матрица С размерностью
![]()
С= =
=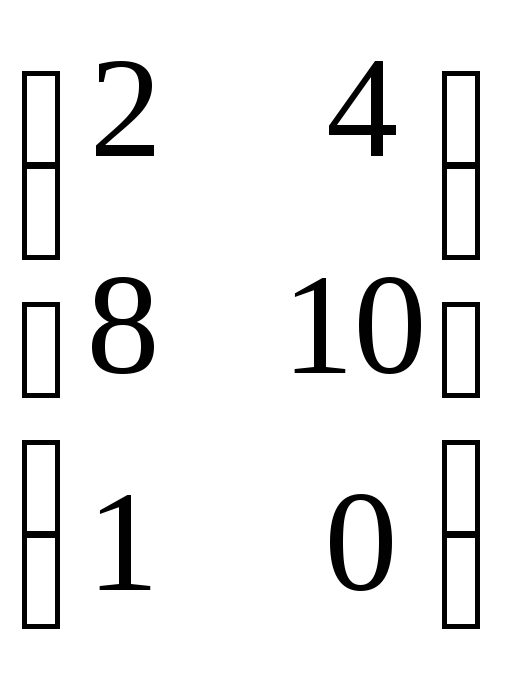 .
.
Замечание. Умножение матриц имеет ряд характерных особенностей:
а) Из существования
произведения
![]() не следует существование произведения
не следует существование произведения![]()
(смотри пример 1.3);
б) Если существуют
матрицы
![]() и
и![]() ,
то их размерности могут не совпадать.
Пусть,
,
то их размерности могут не совпадать.
Пусть,
например,
![]() ,
,![]() ,
тогда
,
тогда![]() и
и![]() ;
;
в) Если существуют
матрицы одинаковой размерности
![]() и
и![]() ,
то не обязательно
,
то не обязательно
![]() =
=![]() .
Показатьсамостоятельно
для матриц
.
Показатьсамостоятельно
для матриц
![]() и
и![]() .
.
г) Произведение двух ненулевых матриц может равняться нулю
![]() ,
,
![]() ,
,![]() (проверить самостоятельно);
(проверить самостоятельно);
5) Возведение матрицы в степень.
Натуральной
степенью
![]() квадратной матрицы
квадратной матрицы![]() называется произведение
называется произведение![]() матриц,
матриц,
равных
![]() :
:![]() .
Кроме того, определим, что
.
Кроме того, определим, что![]() .
Заметим, что из
.
Заметим, что из
уравнения
![]() не следует, что
не следует, что![]() .
Так, например,
.
Так, например,![]() ,
однако
,
однако![]()
(проверить самостоятельно).
6) Транспонирование матриц.
Транспонированной
матрицей к матрице
![]() называется матрица
называется матрица![]() ,
,![]() - я строка которой совпадает с
- я строка которой совпадает с![]() - м столбцом матрицы
- м столбцом матрицы![]() (
(![]() ).
Свойства транспонирования: пусть
).
Свойства транспонирования: пусть![]() и
и![]() - матрицы,
- матрицы,![]() - число, тогда
- число, тогда![]() ;
;![]() ;
;![]() ;
;![]() .
.
Пример 1.4.
Даны матрицы
![]() ,
,![]() .
Найти матрицу
.
Найти матрицу![]() .
.
Решение.
1)
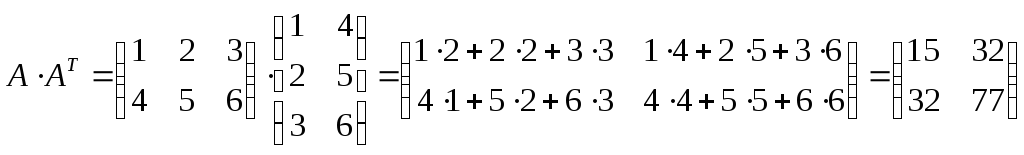 ;
;
2)
![]() ;3)
;3)
![]() +
+![]() =
=
![]() .
.
