2. Параллельные прямые

На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).

Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.

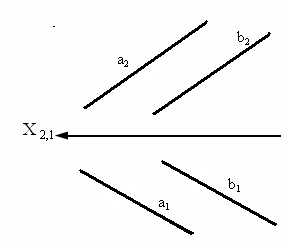
Рис. 3.5. Изображение параллельных прямых

3. Скрещивающиеся прямые

Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.

На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).

Рис. 3. 6. Скрещивающиеся прямые

3.5. Прямая и точка в плоскости

Прямая АВ принадлежит плоскости α, если две ее точки А и В принадлежат этой плоскости α. (∆КLM) Справедливо и обратное утверждение: если точки А и В принадлежат плоскости α,( (∆КLM) то пряма АВ, проходящая через эти точки, принадлежит плоскости α:

Прямые АВ и CD, принадлежащие разным плоскостям показаны на рис. 3. 7. Прямая АВ принадлежит плоской фигуре LKM, потому что на проекциях прямой и плоской фигуры имеются две общих точки. Прямая CD принадлежит плоскости, заданной параллельными прямыми с и d, т. к. она проходит через точки С и D, расположенные на этих прямых.

Прямая принадлежит плоскости, если ее следы принадлежат одновременно следам плоскости.

Справедливо и обратное утверждение: если следы прямой принадлежат следам плоскости, то эта прямая принадлежит плоскости.

Кроме того, существует еще одно свойство, определяющее взаимное положение точки и плоскости: точка принадлежит плоскости, если она расположена на прямой, принадлежащей этой плоскости (рис. 3.7).

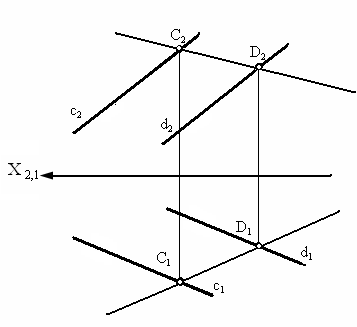
а) б)

Рис. 3.7. Изображение прямых, принадлежащих плоскостям

3.6. Взаимное положение прямой и плоскости

Рассмотрим два случая взаимного положения прямой и плоскости: прямая параллельная и перпендикулярная плоскости.

1. Прямая параллельная плоскости.

Прямая параллельна плоскости, если она параллельна прямой b, принадлежащей этой плоскости. Прямая принадлежит плоскости:

1. если имеет две общих точки;

2. если имеет одну общую точку и параллельна прямой, принадлежащей плоскости.

Прямые, параллельные плоскостям, заданным различными способами показаны на рис. 3.8.

2. Прямая перпендикулярная плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна

двум пересекающимся прямым этой плоскости.

Подробно перпендикулярность прямых рассмотрена в лекции № 4.

а) б)

Рис. 3.8. Прямые, параллельные плоскостям, заданным: а) плоскостью тре-

угольника АВС; б) двумя пересекающимися прямыми а∩b)