14. Анализ динамической устойчивости сар

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после какого-либо воздействия. Для суждения об устойчивости системы практически не требуется находить корней характеристического уравнения, в связи с существованием косвенных признаков, определяющих знаки действительных корней, и тем самым судить об устойчивости. Эти признаки являются критериями устойчивости. существуют следующие критерии устойчивости:

• критерий Рауса;

• критерий Гурвица;

• критерий Михайлова;

• критерий Найквиста.

14. 1. Критерий Рауса

П

(14.1)

редставляет собой систему неравенств, по правилам из коэффициентов характеристического уравнения замкнутой системы. САР будет устойчивой (всеnкорней замкнутой системы будут находиться в левой полуплоскости), если все коэффициенты первого столбца таблицы Рауса (при а₀> 0) будут положительными. Система будет неустойчивой, если хотя бы один из коэффициентов будет отрицательным.

+

+

+

+

+

+

(14.2)

(14.3)

(14.4)

Составим таблицу Рауса:

Согласно критерию устойчивости система является неустойчивой в замкнутом состоянии, т. к. коэффициент с₁₄первого столбца таблицы отрицательный.

14. 2. Критерий Гурвица

Критерий Гурвица является алгебраическим методом, не требующим расчёта корней характеристического, а позволяет определять расположение корней на комплексной плоскости.

Для исследования системы необходимо составить квадратную матрицу из коэффициентов характеристического уравнения.

(14.5)

В главной диагонали записываются коэффициенты полинома от а₁до а_nв порядке возрастания. Вверх от главной диагонали записываются коэффициенты в порядке возрастания, а вниз от главной диагонали – в порядке убывания индексов. На месте отсутствующих коэффициентов записываются 0.

Теорема Гурвица: замкнутая система САР будет устойчивой, если все nчастные определители, составленные из главного определителя Гурвица будут положительными. Система неустойчива, если хотя бы один из частных определителей будет отрицательным.

Частные определители:

Система динамически неустойчива в замкнутом состоянии, т. к. определители , отрицательные.

14. 3. Критерий Михайлова

Критерий Михайлова основан на рассмотрении полинома L(p), при построении АФХ (годограф Михайлова).

(14.6)

U_L(ω) – действительная часть, полученная из членовL(p), содержащих чётные степени р;

V_L(ω) – мнимая часть из членовL(p) с нечётными степенями р.

Годограф Михайлова строят при подстановке ω в U_L(ω), V_L(ω) определяя точки на плоскости. при ω = 0, (jω) = an. При ω→∞, L(jω) неограниченно возрастает. Годограф начинается от действительной оси.

По критерию Михайлова система устойчива, если годограф L(jω) начинается на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно nквадрантов (n– порядок системы).

Запишем полином L(p), как функцию частоты. В уравнение (14.4) подставляем p = jω:

(14.7)

З

(14.8)

апишем уравнение (14.7) в виде (14.6):

(14.9)

(14.10)

Построим годограф, исходя из заданных значений ω, подставляя их в (14.9) и (14.10).

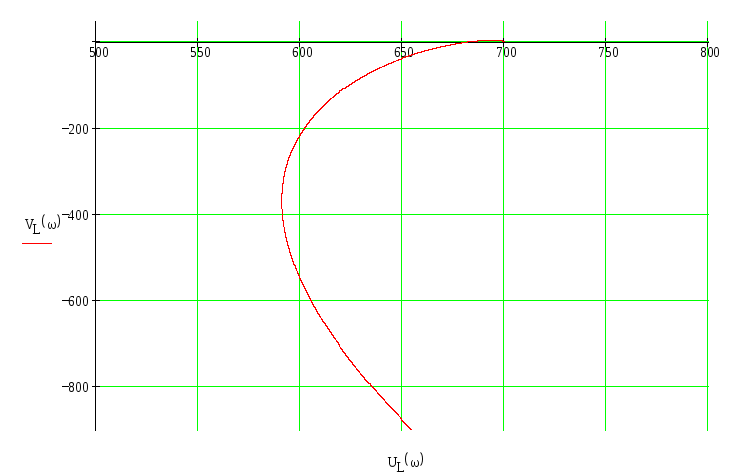
Годограф не охватывает начало координат и нарушает порядок обхода квадрантов, следовательно система неустойчива.