7.2. Передаточная функция дпт.

Так как при фиксированном возбуждении двигатель имеет две степени свободы, то необходимо иметь для него два исходных дифференциальных уравнения.

Первое уравнение может быть получено, если записать второй закон Кирхгофа для цепи якоря:

Второе уравнение представляет собой закон равновесия моментов на валу двигателя:

Где:

- индуктивность и сопротивление цепи якоря;

- коэффициент пропорциональности;

- приведенный к оси двигателя суммарный момент инерции;

- угловая скорость двигателя;

- поток возбуждения;

- момент нагрузки, приведенный к валу двигателя;

Введя оператор дифференцирования и решая уравнения совместно получим:

Где:

- постоянная времени якорной цепи;

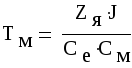- электронно-механическая постоянная времени;

- коэффициент пропорциональности.

Перейдем к углу поворота двигателя,  который связан с угловой скоростью зависимостью:

Тогда:

Где:

- напряжение якоря (регулирующее воздействие);

- момент сопротивления (возмущающее воздействие).

То есть передаточные функции имеют вид:

По регулирующему воздействию:

По возмущающему воздействию:

Где:

- коэффициент передачи двигателя по регули­рующему воздействию

- коэффициент передачи двигателя по возмущаю­щему воздействию

7.3. Передаточная функция сельсинов.

Рассматривая участок статической характеристики сельсинов в диапазоне рабочих углов от 0 до 45, где можно считать характеристику линейной, запишем зависимость напряжения, снимаемого с обмотки ротора сельсина-приемника, от разности углов между осями роторов сельсинов:

тогда передаточная функция:

Где:

- рассогласование (ошибка).

7.4. Передаточная функция усилителя.

Для усилителя, считая его безинерционным звеном можно записать уравнение вида:

откуда передаточная функция:

7.5. Передаточная функция редуктора.

Редуктор преобразует угол поворота  в угол поворота , поэтому, считая его безинерционным звеном запишем передаточную функцию в виде:

Где:

- передаточное отношение редуктора.

8. Структурная схема системы автоматического регулирования.

При составлении структурной схемы САР воспользуемся передаточными функциями элементов системы, полученными в предыдущем разделе.

9. Передаточные функции системы автоматического регулирования.

Для определения передаточных функций систему в разомкнутом состоянии размыкаем систему в точке a (см. структурную схему).

Передаточная функция разомкнутой системы.

где

- добротность системы

Передаточная функция разомкнутой системы по возмущению.

где

Передаточная функция замкнутой системы по задающему воздействию.

Передаточная функция замкнутой системы по возмущающему воздействию.

Передаточная функция замкнутой системы по ошибке от задающего воздействия.

Передаточная функция замкнутой системы по ошибке от возмущающего воздействия.

10. Уравнения динамики замкнутой системы.

Уравнение динамики, разрешенное относительно регулируемой величины, в общем случае имеет вид:

в нашем же случае:

L(p) – характеристический полином замкнутой системы. Характеризует свободное движение объекта и регулятора.

R(p) – операторный полином замкнутой системы, характеризующий влияние задающего воздействия на выходную координату.

S(p) – операторный полином замкнутой системы по возмущающему воздействию, определяет влияние возмущающего воздействия на выходную координату.

Тогда дифференциальное уравнение САР примет вид:

Уравнение динамики, разрешенное относительно ошибки регулирования, в общем случае имеет вид:

в нашем же случае:

Q(p) = L(p) – R(p) – операторный полином.

Тогда дифференциальное уравнение САР примет вид: