2.3. Дифференциальное уравнение равновесия жидкости.

Рассмотрим жидкость, находящуюся в покое относительно неподвижной системы координат хуz. Выделим в этой жидкости элементарный параллелепипед с ребрами dx, dy, dz, параллельными соответствующим осям координат (рис.7). Масса жидкости в параллелепипеде равна dxdydz. Отбросим жидкость, окружающую параллелепипед, и заменим действие отброшенной жидкости сила­ми. Это будут сжимающие поверхностные силы давления.

Кроме поверхностных сил на жидкость действуют массовые силы. Обозначим проекции массовых сил на оси F_x, F_y , F_z.

Отнесенные к единице массы жидкости проекции массовых сил на оси равны:

= F_x/m;

= F_y/m;

= F_z/m;

Давление в центре выделенного объема р. Одинаково действует по всем направлениям. Так как, р является непрерывной функцией координат, определим давление в центрах боковых граней при изменяемой координате например х, и неизменяемым другим:

- в центре левой грани, и

- в центре правой грани.

Аналогичные выражения можно получить для давления в центральных точках других граней.

Составим уравнение равновесия жидкости в форме параллелепипеда. По оси х получим:

F_x+{}dydz-{}dydz=0.

Откуда получаем систему для всех координат:

(2.5)

.

Уравнения этой системы носят названия уравнений равновесия Эйлера.

Для получения полного дифференциала давления умножим уравнения (2.5) на соответствующие приращения координат dx, dy, dz и сложим их:

dx+dy+dz=

В левой части этого уравнения получаем полный дифференциал давления

dp=

(2.6)

2.4. Приборы для измерения давления. Понятие вакуума, абсолютного давления, избыточного давления, недостаточного давления.

Приборы для измерения давления: манометр, вакуумметр, мановакуумметр, альтиометр, барометр, пьезометр и др.

Пьезометр – прибор для измерения давления, состоящий из вертикальной стеклянной трубки, верхний конец которой открыт в атмосферу, а нижний присоединен к объёму жидкости, где измеряется давление.

Н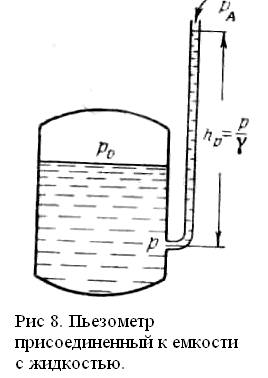а рис.8 представлен открытый в атмосферу пьезометр. Также бывают закрытые, прямые и обратные пьезометры.

Пусть необходимо определить давление р в точке А на уровне z.

Применим основное уравнение гидростатики к точке А и к точке В, расположенной на свободной поверхности жидкости на уровне z₀ (рис.9.). Давление на свободную поверхность равно р₀ – это внешнее давление. р₀ может быть равно атмосферному, быть больше и меньше его.

Из основного уравнения гидростатики:

.

Откуда р=р₀+. Таким образом, давление в точке в покоящейся жидкости равно сумме внешнего давления и давления образованным столбом жидкости. Давление р называют абсолютным давлением жидкости в точке.

Избыточное и вакуумметрическое давление.

Разность р_изб называют избыточным давлением.

ризб =р -рат =р0 + gh - рат

(2.7)

Вакуумметрическое давление р_вак – это разность

рвак = рат – р.

(2.8)

2.5. Энергетическая интерпретация основного закона гидростатики.

Пусть в точке А находится бесконечно малый элемент жидкости dm. Чтобы подняться на высоту h dm необходимо совершить работу:

gh dm.

В точке А элемент dm обладал запасом потенциальной энергии E_п, то есть:

L= E_п==mgh.

Тогда h=E_п/mg-удельная энергия (энергия приходящаяся на единицу массы жидкости).

Таким образом, основное уравнение гидростатики представляет собой удельную энергию жидкости в рассматриваемой точке, где z – удельная потенциальная энергия положения,

- удельная потенциальная энергия давления.