4.1.1. Критерии подобия.

Впервые закон подобия для механических систем был сформу­лирован еще в 1686 году И. Ньютоном, поэтому выражение (92), за­писанное в несколько иной форме, получило название числа, или критерия Ньютона:

(4.5)

При рассмотрении динамически подобных процессов действую­щие в них силы могут быть различны (силы тяжести, вязкости, давления и др.), и одновременное осуществление условия (4.5) для всех этих сил или крайне затруднительно или же просто невозможно. Поэтому в большинстве случаев вопрос решают приближенно - достигают равенства Ne только для основных, доминирующих сил, определяющих характер гидродинамического явления или процесса.

1. Основными являются силы тяжести (это имеет место, напри­мер, при плавании судов, в безнапорных потоках в гидротехни­ческих сооружениях и др.).

Отношение сил тяжести, действующих в двух процессах, может быть выражено следующим образом:

.

Так как для подобия процессов то, приравняв правые части полученного и (4.4) уравнений и сделав сокращения, получим:

или , откуда выразим

Полученная величина u²/gl является безразмерной и представляет собой меру отношения сил инерции к силам тяжести. Эту величину называют числом, или критерием Фруда

(4.6)

2. Основными являются силы трения (это имеет место, например, при напорном движении вязкой жидкости по трубопроводам, дви­жении тел в воздухе и др.).

Отношение сил трения, действующих в двух процессах, в соот­ветствии с законом вязкого трения Ньютона может быть выражено:

.

Приравняв правые части полученного и (4.4) уравнений и сделав сокращения, получим:

.

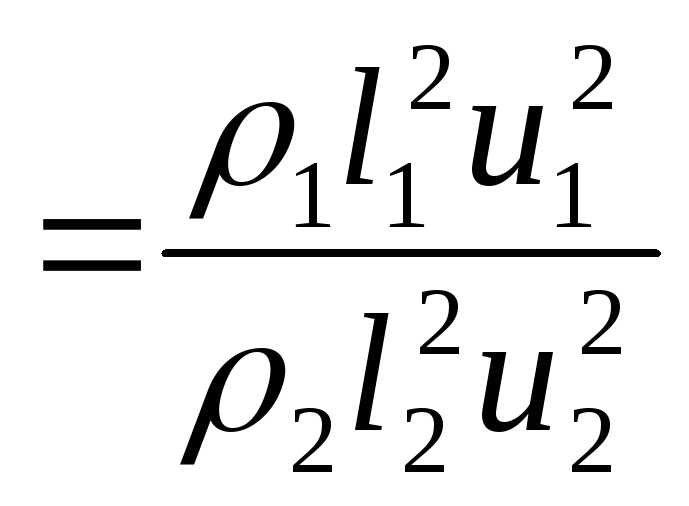Откуда .

Полученная величина является безразмерной и представ­ляет собой меру отношения сил инерции к силам трения. Как уже было сказано выше, эта величина носит название число, или критерий Рейнольдса

(4.7)

3. Основными являются силы давления (это имеет место, напри­мер, в гидравлических прессах, гидравлических приводах объем­ного действия, при исследовании явления кавитации и др.).

Отношение сил давления, действующих в двух процессах, может быть выражено следующим образом:

Приравнивая правые части полученного и (4.4) уравнений и производя сокращения, получим:

Откуда

Полученная величина является безразмерной и представляет собой меру отношения сил давления к силам инерции. Эту величину называют числом, или критерием Эй­лера

(4.8)

4. Безразмерный комплекс Sh. , называемый критерием динамического подобия или числом Струхаля

(4.9)

характеризует отношение сил инерции при неустановившемся движении жидкости к силам инерции конвективной природы. При моделировании неустановившихся движений жидкости нужно соблю­дать равенство чисел Струхаля натуры и модели.

4.2. Режимы движения жидкости.

При движении вязкой жидкости, как показывает опыт, мо­гут существовать два режима течения. Рассмотрим содержание опыта, идея которого принадлежит Рейнольдсу. Бак 1 (рис.29) заполнен жидкостью, которая может течь по трубе 2 с прозрач­ными стенками с различными скоростями в зависимости от сте­пени открытия крана 3. Сосуд 4 заполнен подкрашенной жидко­стью для визуализации течения основной жидкости в баке. Если скорость потока в трубе незначительна, подкрашенные частицы движутся четкой струйкой, как показано на рис.29,а. До опре­деленного предела увеличения скорости никаких качественных изменений течения не произойдет, однако, начиная с некоторой скорости, четко обозначенная струйка начинает размываться (рис.29,б), и в результате перемешивания весь поток жидкости в трубе сказывается подкрашенным. Слоистое течение без перемешивания слоев жидкости (см. рис.29,а) называется ламинарным; течение с интенсивным перемешиванием слоев жидкости между собой (см. рис.29,6) называется турбулентным.

Опыты показали, что переход практически однозначно определяется величиной числа Рейнольдса:

,

где U_ср - средняя скорость.

Если Re меньше некоторого критического значения Re_Kp то режим течения ламинарный; при Re>Re_Kp течение турбу­лентно. Опыты, проведенные при обычных условиях, дают зна­чение критического числа Рейнольдса для круглых труб: Re_Kp= 2320. При числе Рейнольдса Rе>Re_Kp - режим движе­ния переходит в турбулентный. Переход ламинар­ного режима течения в турбулентный связан с потерей устойчи­вости потока, которая зависит не только от числа Рейнольдса, но и от интенсивности случайных возмущений, вносимых в по­ток.