
- •СОДЕРЖАНИЕ
- •2.Теоретический материал по темам курса
- •2.5.Расчет движущихся с ускорением элементов конструкций
- •3.1.2.Задача №2
- •Пример выполнения задачи №2
- •3.2.Расчеты на сложное сопротивление
- •3.2.1.Задача №3
- •Пример выполнения задачи №3
- •Пример выполнения задачи №4
- •4.1.Задача №1
- •6.Рекомендуемая литература
- •6.Приложения
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
pн |
|
|
|
|
|
P |
|
|
|
|
e |
P |
|
|
|
|
|
d |
D |
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
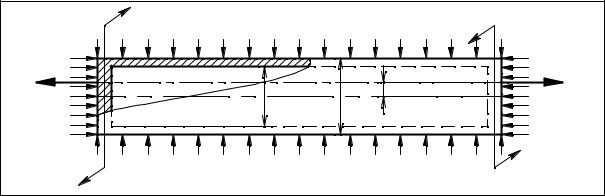
Рис.3.13 |
|
4 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Пример выполнения задачи №4 |
|
||
|
|
Рассмотрим решение задачи со следующими исходными данными: |
||||||
pн = 4МПа; m =10 кНм; P = 50 кН ; |
e = 80 мм; D =165 мм; d = 159 мм; |
|||||||
σТр = 250 МПа; σТс = 300МПа, (схема 4 рис.3.13). |
|
|||||||
|
|
Решение. 1).Определим необходимые для дальнейшего расчета гео- |
||||||
метрические характеристики тонкостенной трубы: |
|
|||||||
Толщина стенки трубы - t = (D −d )/ 2 = (165 −159)/ 2 = 3 мм; |
|
|||||||
Средний диаметр трубы как тонкостенной оболочки – |
|
|||||||
Dср = (D + d )/ 2 = |
(165 +159)/ 2 =162 мм; |
|
|
|||||
Площадь поперечного сечения – |
|
|
|
|||||
F =π (D2 −d 2 )/ 4 = 3.14 (1652 −1592 )/ 4 =1526 мм2 ; |
|
|||||||
Момент сопротивления поперечного сечения изгибу – |
|
|||||||
W =πD3 |
(1 −(d / D)4 )/ 32 = 3.14 1653 (1 −(159 /165)4 )/ 32 =60701 мм3 ; |
|||||||
Момент сопротивления поперечного сечения кручению – |
|
|||||||
Wρ =πD3 (1 −(d / D)4 )/16 = 3.14 1653 (1 −(159 / 165)4 )/ 16 = 121403 мм3. |
||||||||
|
|
2).Рассчитаем напряжения в трубе как в стержне: |
|
|||||
Максимальные касательные напряжения кручения (на поверхности) – |
||||||||
τ |
кр |
= M |
кр |
/W = m |
/W = 10 106 / 121403 = 82.4 МПа; |
|
||
|
|
ρ |
ρ |
|
|
|
||
Максимальные нормальные напряжения изгиба – |
|
|||||||
σи = M /W = P e /W = 50 103 80 / 60701 = 65.9 МПа; |
|
|||||||
Нормальные напряжения растяжения (от нормальной силы) – |
|
|||||||
σ р = N / F = P / F = 50 103 /1526 = 32.8 МПа. |
|
|
||||||
|
|
3).Рассчитаем напряжения в трубе как в тонкостенной (безмоментной) |
||||||
оболочке вращения. Оболочка нагружена внешним давлением вызываю- |
||||||||
щим ее сжатие, поэтому давление принимается отрицательным |
p = −pн . |
|||||||
Главные радиусы кривизны оболочки: в меридиональном сечении |
ρm = ∞; |
|||||||
в окружном сечении ρt = Dср / 2 = 81 мм. Подставляя эти значения в урав- |
||||||||
|
|
|
|
|
89 |
|
|
|

нение Лапласа (2.52) получим |
σt + |
σm = |
−pн , откуда окружное напряже- |
|||||
|
|
−pнρt |
|
4 81 |
|
ρt |
∞ |
t |
ние |
σt = |
= − |
= −108 МПа. Для определения меридионального |
|||||
|
|
t |
|
3 |
|
|
|
|
напряжения σm используем формулу (2.53), для этого рассмотрим равно-
весие части трубы, отсеченной поперечным сечением в проекции, на ось самой трубы. В формуле (2.53) ϕ = 90°, sinϕ = 1, а суммарная проекция давления действующего на поверхность отсеченной части трубы будет равна - P = −pнFт = −pнπDср2 / 4 = −pнπρt2 , так как на ось трубы будет проецироваться давление, действующее только на поверхности (площадьюFт), закрывающие торцы трубы. Тогда согласно формуле (2.53), мери-
|
−p πρ2 |
|
−p ρ |
|
|
σ |
|
|
диональное напряжение σm = |
н t |
= |
н |
t |
= |
|
t |
= −54 МПа. |
2πρt t |
|
|||||||
|
|
2 t |
|
|
2 |
|
||
4).Определим главные напряжения. Материал трубы находится в плоском напряженном состоянии, достаточно взять произвольную точку на поверхности трубы (именно на поверхности возникают максимальные напряжения). В любой точке возникают нормальные напряжения в продольном (параллельно оси) направлении обозначим их - σx , и в направле-
нии перпендикулярном оси трубы обозначим их - σ y . Кроме того, в плоскости XY действуют касательные напряжения τxy . В плоскости перпендикулярной плоскости XY возникают нормальные напряжения порядка pн и могут не учитываться в силу малости.
|
Продольные нормальные напряжения складываются из напряжений |
|||||
растяжения, |
изгиба и меридиональных - σx =σ р ±σи +σm их максималь- |
|||||
ное |
и |
минимальное |
значения |
равны |
соответственно: |
|
σx max = 32.8 +65.9 −54 = 44.7 МПа; |
σx min = 32.8 −65.9 −54 = −87.1 МПа. |
|||||
Напряжения |
σ y равны окружному |
σ y =σm = −54 МПа. |
Максимальные |
|||
касательные напряжения равны τxy =τкр = 82.4 МПа. Используя выраже-
ние (2.15), рассчитаем главные напряжения с учетом правила их индексации и то, что одно из главных напряжений равно нулю. Для точки 1, с максимальными продольными напряжениями:
σ1 |
= |
44.7 −54 |
+ |
|
44.7 |
−(−54) |
|
2 |
+ = 91.4 МПа; |
σ2 =0 МПа; |
|||||
2 |
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
σ3 |
= |
44.7 |
− |
54 |
− |
|
44.7 |
− |
( |
−54 |
) |
|
2 |
+82.42 = −100.7 МПа, |
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для точки 2, с минимальными продольными напряжениями:
90
